変形オイラーの方程式における重積分の扱いについて
変形オイラーの方程式における重積分の扱いについて
YAS_YAS さんの書込 (2009/07/12(Sun) 15:37)
はじめまして,YAS_YASと申します.m(_ _)mペコ
某社の技術職をしています. 数学が苦手なので,このサイトでいつも勉強させて頂いております.
この数日間, googleなどのネット情報,本屋,図書館など考えられる限りの文献を 当たってみたのですが,解決の糸口が見つからないので投稿させて頂きました.
悩んでいる問題ですが, このサイトの「物理数学/変分法2」で取り上げている 「色々な変形オイラー方程式」の7番です
この項では,それまで1つだった独立変数を2つに拡張した場合のオイラー方程式を 扱っており,汎関数を次式としてしています.
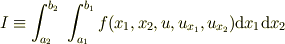
ここで, 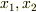 が独立変数で,
が独立変数で,  は従属変数です.
は従属変数です.
 の微小な変化を,
任意の微小量
の微小な変化を,
任意の微小量  と任意の関数
と任意の関数 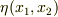 を使って
を使って
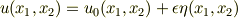
としているので,  の
の 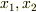 による偏微分
による偏微分 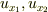 も従属変数になります.
も従属変数になります.
汎関数の  による微小変化を使って,停留値問題に持ち込んでおり
による微小変化を使って,停留値問題に持ち込んでおり
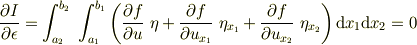
として,右辺の第二項,第三項を 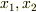 で部分積分する流れになっています.
で部分積分する流れになっています.
ここまでは従来通りの流れなので,ついていけたのですが, 重積分の部分積分をした次の式で,わたしの理解が破たんしました. (重積分の部分積分をした経験はわたしにはありません)
![\left[\frac{\partial f}{\partial u_{x_1}}\ \frac{\partial^2 \eta}{\partial x_1^2}\ \right]_{a_1}^{b_1}+\left[\frac{\partial f}{\partial u_{x_2}}\ \frac{\partial^2 \eta}{\partial x_2^2}\ \right]_{a_2}^{b_2}+\int_{a_2}^{b_2}\ \int_{a_1}^{b_1}\left\{\frac{\partial f}{\partial u}-\frac{\mathrm{d}}{\mathrm{d} x_1}\left(\frac{\partial f}{\partial u_{x_1}}\right)-\frac{\mathrm{d}}{\mathrm{d} x_2}\left(\frac{\partial f}{\partial u_{x_2}}\right)\right\}\ \eta\mathrm{d}x_1\mathrm{d}x_2](http://hooktail.maxwell.jp/bbslog/2504421bb008077c7af7e90976173358.png)
まず,第一項の中身ですが,従来ならば
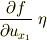
のように,右側の項は積分された形になり,第三項の
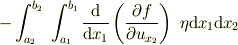
の 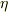 に対応しなければ,
後で
に対応しなければ,
後で 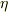 について括りだせないはずです.ところが実際は
について括りだせないはずです.ところが実際は
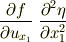
のように,逆に 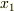 でさらに偏微分した形になっています.
でさらに偏微分した形になっています.
また,積分範囲が 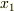 の範囲だけで,
の範囲だけで,
![\left[\frac{\partial f}{\partial u_{x_1}}\ \frac{\partial^2 \eta}{\partial x_1^2}\ \right]_{a_1}^{b_1}](http://hooktail.maxwell.jp/bbslog/9ac102faca37afc618f25c7fbeaa4f06.png)
のようになされているのですが,このとき 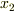 側の積分範囲の扱い
はどうなるのでしょう?
項自体は定数になるはずなので,項中の
側の積分範囲の扱い
はどうなるのでしょう?
項自体は定数になるはずなので,項中の 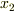 には
には 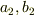 の値が何らかの形で入るはずと思われるのですが,
の値が何らかの形で入るはずと思われるのですが,
![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) 内は1項しか存在してないので,
内は1項しか存在してないので,
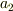 を代入した項,
を代入した項,  を代入した項と分かれているわけでもないようです.
また,単に
を代入した項と分かれているわけでもないようです.
また,単に  という係数が掛けられているわけでもなく,
どのように扱われているのかがわかりません.
右辺,第二項についても同様のことが言えます.
という係数が掛けられているわけでもなく,
どのように扱われているのかがわかりません.
右辺,第二項についても同様のことが言えます.
調べた文献では,
境界条件としてあらかじめこの ![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) の項が消去されているか,
まったく触れずに,消去されているかのどちらかで取り付く島がありませんでした.
そもそも,端点が固定されていても
の項が消去されているか,
まったく触れずに,消去されているかのどちらかで取り付く島がありませんでした.
そもそも,端点が固定されていても 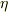 の端点における
二階偏微分の値が0になる保証はないと思うのですが.
の端点における
二階偏微分の値が0になる保証はないと思うのですが.
以上,長文となってしまって恐縮ですが, 質問は究極的には 「重積分の部分積分の仕方をご教示ください」 ということになります.
上に挙げた疑問点も加えてまとめると
![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) 内の右側の項
内の右側の項 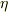 の形が異なるのはなぜか?
の形が異なるのはなぜか?
2) ![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) の積分範囲は1つの独立変数のものだが,もう片方の扱いは?
3)端点を固定しているという境界条件だけでは,
の積分範囲は1つの独立変数のものだが,もう片方の扱いは?
3)端点を固定しているという境界条件だけでは, ![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) を0にするには無理がないか?
を0にするには無理がないか?
ということになります.
ご教示のほど,よろしくお願いいたします.m(_ _)m
Re: 変形オイラーの方程式における重積分の扱いについて
yama さんのレス (2009/07/12(Sun) 18:25)
記事のその部分は間違っているように思われます. YAS_YASさんが書かれているように第一項の中身は

になると思います.
ただし積分の両端でのこの量の差をとるのではなく,この量と第二項から出てくる同様な量についての線積分をとることになります.
つまり,部分積分によって面積分の一部が線積分に変わるわけです.
具体的には,平面のグリーンの定理( http://www12.plala.or.jp/ksp/vectoranalysis/GreensTheorem/ )を利用します.
線積分は面積分の領域の境界上の積分になりますが,積分領域の境界では(境界値が固定されているため) 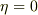 なので,この線積分は0になるわけです
なので,この線積分は0になるわけです
Re: 変形オイラーの方程式における重積分の扱いについて
YAS_YAS さんのレス (2009/07/13(Mon) 19:27)
yamaさん
ご回答ありがとうございます.m(_ _)mペコ
返信が遅くなってしまって,すいません(会社からこの掲示板が見れないことが判明!)
なるほど,面積分が平面のグリーンの定理によって,線積分に変換されているので 積分区間が,一方の独立変数のものだけで済むのですね.
ということは,
![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) 内は,その独立変数のみの関数となっているのでしょうか?
内は,その独立変数のみの関数となっているのでしょうか?
いずれにしても,境界条件の 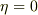 でこの項は消去されてしまいますので,
結果としては,問題ないことになってしまいますね.
でこの項は消去されてしまいますので,
結果としては,問題ないことになってしまいますね.
ただ,この方法が有効なのは独立変数が2つまでに限定されてしまっているのが,多少気になるところです. 一般に独立変数がn個などとなった場合はどうなってしまうのでしょう?
...と,まずは2個の場合をきっちりと理解してみます (^-^)/ どうも,ありがとうございました.
Re: 変形オイラーの方程式における重積分の扱いについて
yama さんのレス (2009/07/13(Mon) 22:56)
[]ではなくて線積分になるということです.つまり
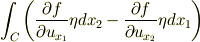
になるわけです.積分経路Cは積分領域の境界となる閉曲線です. 本例では積分領域が長方形なので,長方形の各辺に沿って一周する線積分になります.
なお,この方法は独立変数が2個までに限定されるわけではありません. 独立変数がn個の場合にn次元空間の所定の領域での積分の極値を求めるとします. 変分をとって部分積分を行うと,積分の一部が積分領域の境界面(n-1次元の超曲面)上の積分に変わります.境界値が固定されているのでこの積分は0になります.
Re: 変形オイラーの方程式における重積分の扱いについて
YAS_YAS さんのレス (2009/07/13(Mon) 23:55)
yamaさん
重ねて,ご回答ありがとうございます.m(_ _)mペコ
今ちょうど,取り組んでいたところでした.
確かに平面のグリーンの定理を使うと,もはや ![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) の概念では
なさそうだな(あるいは概念の拡張?)というところまでは,
なんとなく到達したのですが,yamaさんの回答で自信がついたところです (^-^)/
の概念では
なさそうだな(あるいは概念の拡張?)というところまでは,
なんとなく到達したのですが,yamaさんの回答で自信がついたところです (^-^)/
自信がついた矢先に,独立変数が  個の場合の話であっけなく自信が崩壊しましたが...(笑)
個の場合の話であっけなく自信が崩壊しましたが...(笑)
「重積分→線積分」といったように,次元を1つ落として議論していくんだなと
発想自体は漠然とはわかるのですが,
 次元の超曲面を
次元の超曲面を 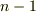 次元の超曲面上の積分に置き代える手順がわかりません.
次元の超曲面上の積分に置き代える手順がわかりません.
重積分を線積分に変換した, 平面のグリーンの定理にあたる,定理が存在するのでしょうか?
もはや,どのカテゴリー(ベクトル解析,変分など)を調べれば良いのか 見当がつかなくなってしまっているので, 勉強をするのに良い本などを紹介いただけると幸いです.
よろしくお願いいたします.m(_ _)mペコ
Re: 変形オイラーの方程式における重積分の扱いについて
yama さんのレス (2009/07/14(Tue) 00:28)
例えば,3次元空間の積分は,ガウスの定理によって積分領域の境界面上の面積分に変換されます. ガウスの定理はn次元の場合にも一般化されます.
変分法については,変分法の専門書がいろいろあるようですが,その内容については私は詳しいことは分かりません. 書店や図書館などで適当なものを捜すのがよいと思います.
Re: 変形オイラーの方程式における重積分の扱いについて
YAS_YAS さんのレス (2009/07/15(Wed) 02:13)
yamaさん,Hiroさん
ご回答ありがとうございます.m(_ _)mペコ
おかげさまで,理解できたと思います.多分...(汗)
以下,理解した範囲でまとめたものです
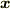 は独立変数
は独立変数 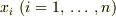 を要素とする
を要素とする  次元ベクトル
次元ベクトル
 は
は 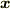 を引数にとるスカラー関数で,次式で表す
を引数にとるスカラー関数で,次式で表す
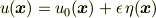
ここで,  は任意の微小量,
は任意の微小量, 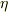 は
は 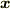 を引数にとる任意のスカラー関数である
を引数にとる任意のスカラー関数である
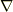 を成分表示すれば次式となる
を成分表示すれば次式となる
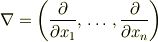
したがって,  の偏導関数は
の偏導関数は 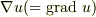 と書け,
と書け,  次元ベクトルとなる
次元ベクトルとなる
汎関数を次式とする
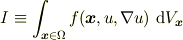
ここで, 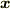 は独立変数,
は独立変数, 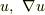 は従属変数
は従属変数
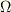 は
は 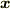 が定義されるベクトル場を含むある領域で
が定義されるベクトル場を含むある領域で
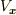 は次式
は次式
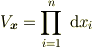
 に関して変分をとると次式となる
に関して変分をとると次式となる
![\left. \frac{\mathrm{d}I[u]}{\mathrm{d}\epsilon}\right|_{\epsilon=0} = \int_{\bm{x}\in\Omega} \left(\frac{\partial f}{\partial u}\,\eta + \frac{\partial f}{\partial (\nabla u)}\cdot \nabla \eta \right)\mathrm{d}V_{\bm{x}}](http://hooktail.maxwell.jp/bbslog/8f5f4fbd760887f9bfff51ef7b9fb1e4.png)
(所見1) ここで,
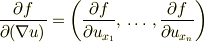
の意味だと思うのですが,偏微分の分母の部分にベクトル( 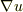 )が来る表記法があるのですね.初めて見ました.
)が来る表記法があるのですね.初めて見ました.
話を戻して,次の関係を変分の式に適用すると
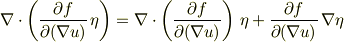
下のように変形できる
![\left. \frac{\mathrm{d}I[u]}{\mathrm{d}\epsilon}\right|_{\epsilon=0}&=\ \int_{\bm{x}\in\Omega} \left\{\frac{\partial f}{\partial u}\,\eta +\nabla \cdot \left(\frac{\partial f}{\partial (\nabla u)}\,\eta \right)-\nabla \cdot \left(\frac{\partial f}{\partial (\nabla u)}\right)\,\eta\right\}\mathrm{d}V_{\bm{x}}\\&=\ \int_{\bm{x}\in\Omega} \nabla \cdot \left(\frac{\partial f}{\partial (\nabla u)}\,\eta \right)\mathrm{d}V_{\bm{x}}+\int_{\bm{x}\in\Omega} \left\{\frac{\partial f}{\partial u}-\nabla \cdot \left(\frac{\partial f}{\partial (\nabla u)}\right)\right\}\,\eta \ \mathrm{d}V_{\bm{x}}\\&=\ \oint_{\bm{x}\in\partial \Omega} \mathrm{d}\bm{S_{x}}\cdot\left(\frac{\partial f}{\partial (\nabla u)}\,\eta \right)+\int_{\bm{x}\in\Omega} \left\{\frac{\partial f}{\partial u}-\nabla \cdot \left(\frac{\partial f}{\partial (\nabla u)}\right)\right\}\,\eta \ \mathrm{d}V_{\bm{x}}](http://hooktail.maxwell.jp/bbslog/7051f1c144b510533ff5199e796fae9b.png)
(所見2)
この部分が部分積分に当たるのですね
2行目から,3行目で第1項目にガウスの定理を適用している部分が
かつて ![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) の定積分の箇所に相当し,境界条件で消去されるわけですね
の定積分の箇所に相当し,境界条件で消去されるわけですね
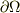 は領域
は領域 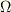 の全表面を表しているという認識でよろしいのでしょうか?
の全表面を表しているという認識でよろしいのでしょうか?
話を戻して,停留条件から
![\left. \frac{\mathrm{d}I[u]}{\mathrm{d}\epsilon}\right|_{\epsilon=0}&=\ \int_{\bm{x}\in\Omega} \left\{\frac{\partial f}{\partial u}-\nabla \cdot \left(\frac{\partial f}{\partial (\nabla u)}\right)\right\}\,\eta \ \mathrm{d}V_{\bm{x}}\ = \ 0](http://hooktail.maxwell.jp/bbslog/6b6e8a3d6f720c57beef5a5f86e4e081.png)
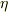 の任意性から,括弧内が
の任意性から,括弧内が 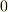 になるしかないので
になるしかないので
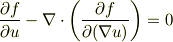
となり,  次元の独立変数をもつ場合の,変形オイラーの方程式が導けました (^-^)/
次元の独立変数をもつ場合の,変形オイラーの方程式が導けました (^-^)/
(所見3) 導出した式を,今までのオイラーの方程式と比較して違和感を持つのが, 左辺第二項目を成分表示した場合の

という微分の部分が
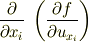
のように偏微分の形になっている点です. この部分の解釈が,現時点で一番判然としないところです 独立変数が3個以上(三重積分以降)はこのような形が一般的なのでしょうか?
いま一つ, 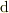 と
と 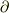 の区分けが
理解できていないので稚拙な質問かと思いますが,ご教示頂ければ幸いです.
の区分けが
理解できていないので稚拙な質問かと思いますが,ご教示頂ければ幸いです.
いずれにしても,お二人のおかげで この数日で,ヨチヨチ歩きから,二足歩行に進化した気分です (^-^)
どうも,ありがとうございます.
Re: 変形オイラーの方程式における重積分の扱いについて
yama さんのレス (2009/07/15(Wed) 10:50)
正しく理解されていると思います.
常微分と偏微分についてですが,独立変数が2個以上の場合は偏微分を用います.
「物理数学/変分法2」では,2変数の場合も常微分を用いていますが,正しくは偏微分にすべきだと思います.
多変数の場合にも常微分を用いることがありますが,それは変数の間に関数関係があって独立変数が実際には1つだけになるような場合です.
変分を考える場合には,変数 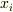 の間には何の関数関係も仮定されていないので,2変数以上の場合は偏微分を用いないといけません.
の間には何の関数関係も仮定されていないので,2変数以上の場合は偏微分を用いないといけません.
Re: 変形オイラーの方程式における重積分の扱いについて
toorisugari no Hiro さんのレス (2009/07/15(Wed) 12:40)
細かい部分だけ
> 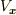 は次式
は次式 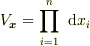
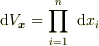
> |9a903231c3cf1ae239da2d13614b1796|
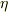 が見える形が望ましいです.また,この書き方だと右辺は
が見える形が望ましいです.また,この書き方だと右辺は 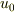 での微分で書かなければいけません.
での微分で書かなければいけません.
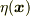 として
として  とすると,従来の汎関数微分になりますね.
(
とすると,従来の汎関数微分になりますね.
( 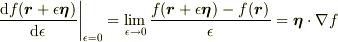 (方向微分)から
(方向微分)から 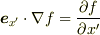 (偏微分)へ.)
(偏微分)へ.)
> 話を戻して,次の関係を変分の式に適用すると > |2694ffd942017cccca31a6368dd62962|
最後の項は内積にしてください. これは
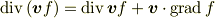
という公式に当たります.
> |7b8b965ad4bca0e41ab51de7b31363a1| 次元の独立変数をもつ場合の,変形オイラーの方程式が導けました (^-^)/
 次元の一個を時間に取れば,通常の場のEL方程式になりますね.
次元の一個を時間に取れば,通常の場のEL方程式になりますね.
> ここで, > |9da02537f7ef7a4475f9ce4ad897333b| > の意味だと思うのですが,偏微分の分母の部分にベクトル( |f3979972f6f5cbda44027bb950895406| )が来る表記法があるのですね.初めて見ました.
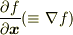 という記法と同じです.
という記法と同じです.
後のご質問やご確認は「その通りです.」
Re: 変形オイラーの方程式における重積分の扱いについて
YAS_YAS さんのレス (2009/07/16(Thu) 00:04)
yamaさんHiroさん
毎度,お世話になっております.m(_ _)mペコ
きめ細かい回答,ありがとうございます (^-^)/
yamaさんへ
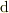 と
と 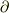 の違いに関する説明は,
目からウロコが落ちました気分です.
の違いに関する説明は,
目からウロコが落ちました気分です.
式上,見た目が同じでも,
相互に関係式が持たれていて,最終的に1つの独立変数に帰着できる場合は 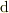 相互に関係式を持つことなく,最後まで変数が独立を保っている場合は
相互に関係式を持つことなく,最後まで変数が独立を保っている場合は 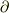 となるわけですね.なにかピタリとはまった感じがします.
となるわけですね.なにかピタリとはまった感じがします.
Hiroさんへ
誤記の嵐で,お恥ずかしい限りです(^-^;)
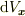 の部分は完全にわたしの誤記です
あと,
の部分は完全にわたしの誤記です
あと,
 の部分も,内積であるとわかりつつ
の部分も,内積であるとわかりつつ  が抜けてました
が抜けてました
ただ,ご紹介いただいた公式は知らなかったので,結果的には間違って良かったなぁと(笑)
![\left. \frac{\mathrm{d}I[u]}{\mathrm{d}\epsilon} \right|_{\epsilon=0}](http://hooktail.maxwell.jp/bbslog/919fc7ba47d4bf138c72d5daff58958c.png) の部分の
の部分の  の部分は,確かに何も考えずに書いてました.
の部分は,確かに何も考えずに書いてました.
以前,Hiroさんが回答して下さったものを見ると, ![\left. \frac{\mathrm{d}I[u+\epsilon\,\eta]}{\mathrm{d}\epsilon} \right|_{\epsilon=0}](http://hooktail.maxwell.jp/bbslog/36be685b1bd1388efee6ba7a868f6b2b.png) という記述になっており,
理解が不十分だったと痛感しております(今も不十分ですが).
という記述になっており,
理解が不十分だったと痛感しております(今も不十分ですが).
以前調べた文献の中に  の表現を,
の表現を, 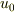 を使わずに
を使わずに
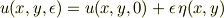
としていたものがあったのですが,今考えてみると ![\left. \frac{\mathrm{d}I[u]}{\mathrm{d}\epsilon} \right|_{\epsilon=0}](http://hooktail.maxwell.jp/bbslog/919fc7ba47d4bf138c72d5daff58958c.png) と書くための布石だったのかなと,思いました.
と書くための布石だったのかなと,思いました.
実はわたし,恥ずかしながら「汎関数微分」なる用語を今回初めて知りました(汗) 今後の課題としたいと思ってます.
おかげさまで,変形オイラー法について,質問当初に比べて, かなり地に足がついたイメージが持てたと思います (^-^)/
これもお二人の丁寧なご指導のたまものです! ありがとうございました.m(_ _)mペコ

![I[u] &\equiv \int_{\bm{x}\in\Omega} f(\bm{x}, u, \nabla u) \mathrm{d}V_{\bm{x}}](http://hooktail.maxwell.jp/bbslog/ca4c7f403f865c1e76d00c16e948e04d.png)
![\left. \frac{ \mathrm{d}I[u+\epsilon\eta] }{ \mathrm{d}\epsilon }\right|_{\epsilon=0} &= \int_{\bm{x}\in\Omega} \left.\frac{ \mathrm{d} f(\bm{x}, u+\epsilon\eta, \nabla u+\epsilon\nabla\eta)}{ \mathrm{d}\epsilon }\right|_{\epsilon=0} \mathrm{d}V_{\bm{x}}\\&= \int_{\bm{x}\in\Omega} \left \{ \frac{\partial f}{\partial u}\eta + \frac{\partial f}{\partial (\nabla u)} \cdot \nabla \eta \right \} \mathrm{d}V_{\bm{x}}\\ &= \int_{\bm{x}\in\Omega} \left \{\frac{\partial f}{\partial u}\eta + \nabla \cdot \left (\frac{\partial f}{\partial (\nabla u)} \eta \right)- \left ( \nabla \cdot \frac{\partial f}{\partial (\nabla u)} \right) \eta\right\} \mathrm{d}V_{\bm{x}}\\ &= \oint_{\bm{x}\in\partial \Omega} \mathrm{d}\bm{S}_{\bm{x}} \cdot \left (\frac{\partial f}{\partial (\nabla u)} \eta \right)+ \int_{\bm{x}\in\Omega} \left (\frac{\partial f}{\partial u} - \nabla \cdot \frac{\partial f}{\partial (\nabla u)} \right) \eta\, \mathrm{d}V_{\bm{x}}](http://hooktail.maxwell.jp/bbslog/050828e7962543c653f7a0d29d8ec89d.png)