変形オイラーの方程式における重積分の扱いについて
変形オイラーの方程式における重積分の扱いについて
YAS_YAS さんの書込 (2009/07/12(Sun) 15:14)
はじめまして,YAS_YASと申します.m(_ _)mペコ
某社の技術職をしています. 数学が苦手なので,このサイトでいつも勉強させて頂いております.
この数日間, googleなどのネット情報,本屋,図書館など考えられる限りの文献を 当たってみたのですが,解決の糸口が見つからないので投稿させて頂きました.
悩んでいる問題ですが, このサイトの「物理数学/変分法2」で取り上げている 「色々な変形オイラー方程式」の7番です
この項では,それまで1つだった独立変数を2つに拡張した場合のオイラー方程式を 扱っており,汎関数を次式としてしています.
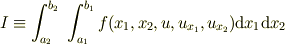
ここで, 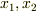 が独立変数で,
が独立変数で,  は従属変数です.
は従属変数です.
 の微小な変化を,
任意の微小量
の微小な変化を,
任意の微小量  と任意の関数
と任意の関数 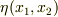 を使って
を使って

としているので,  の
の 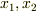 による偏微分
による偏微分 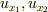 も従属変数になります.
も従属変数になります.
汎関数の<tex?epsilon</tex> による微小変化を使って,停留値問題に持ち込んでおり
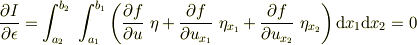
として,右辺の第二項,第三項を 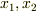 で部分積分する流れになっています.
で部分積分する流れになっています.
ここまでは従来通りの流れなので,ついていけたのですが, 重積分の部分積分をした次の式で,わたしの理解が破たんしました. (重積分の部分積分をした経験はわたしにはありません)
![\left[\frac{\partial f}{\partial u_{x_1}}\ \frac{\partial^2 \eta}{\partial x_1^2}\ \right]_{a_1}^{b_1}+\left[\frac{\partial f}{\partial u_{x_2}}\ \frac{\partial^2 \eta}{\partial x_2^2}\ \right]_{a_2}^{b_2}+\int_{a_2}^{b_2}\ \int_{a_1}^{b_1}\left\{\frac{\partial f}{\partial u}-\frac{\mathrm d}{\mathrm x_1}\left(\frac{\partial f}{\partial u_{x_1}}\right)-\frac{\mathrm d}{\mathrm x_2}\left(\frac{\partial f}{\partial u_{x_2}}\right)\right\}\ \eta\mathrm{d}x_1\mathrm{d}x_2](http://hooktail.maxwell.jp/bbslog/b93ad8c774a35e9b3b0a03d027a51b14.png)
まず,第一項の中身ですが,従来ならば
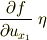
のように,右側の項は積分された形になり,第三項の
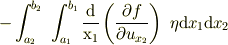
の 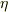 に対応しなければ,
後で
に対応しなければ,
後で 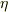 について括りだせないはずです.ところが実際は
について括りだせないはずです.ところが実際は
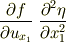
のように,逆に 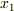 でさらに偏微分した形になっています.
でさらに偏微分した形になっています.
また,積分範囲が 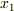 の範囲だけで,
の範囲だけで,
![\left[\frac{\partial f}{\partial u_{x_1}}\ \frac{\partial^2 \eta}{\partial x_1^2}\ \right]_{a_1}^{b_1}](http://hooktail.maxwell.jp/bbslog/9ac102faca37afc618f25c7fbeaa4f06.png)
のようになされているのですが,このとき 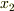 側の積分範囲の扱い
はどうなるのでしょう?
項自体は定数になるはずなので,項中の
側の積分範囲の扱い
はどうなるのでしょう?
項自体は定数になるはずなので,項中の 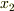 には
には 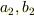 の値が何らかの形で入るはずと思われるのですが,
の値が何らかの形で入るはずと思われるのですが,
![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) 内は1項しか存在してないので,
内は1項しか存在してないので,
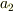 を代入した項,
を代入した項, 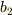 を代入した項と分かれているいるわけでもないようです.
また,単に
を代入した項と分かれているいるわけでもないようです.
また,単に  という係数が掛けられているわけでもないので
どのように扱われているのかもわかりません.
右辺,第二項についても同様のことが言えます.
という係数が掛けられているわけでもないので
どのように扱われているのかもわかりません.
右辺,第二項についても同様のことが言えます.
調べた文献では,
境界条件としてあらかじめこの ![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) の項が消去されているか,
まったく触れずに,消去されているかのどちらかで取り付く島がありませんでした.
そもそも,端点が固定されていても
<tex>eta<tex>の端点における
二階偏微分の値が0になる保証はないと思うのですが.
の項が消去されているか,
まったく触れずに,消去されているかのどちらかで取り付く島がありませんでした.
そもそも,端点が固定されていても
<tex>eta<tex>の端点における
二階偏微分の値が0になる保証はないと思うのですが.
以上,長文となってしまって恐縮ですが, 質問の究極部分は
『重積分の部分積分の仕方をご教示ください』
ということになりますが,以上に挙げた疑問点も加えてまとめると
![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) 内の右側の項
内の右側の項 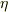 の形が異なるのはなぜか?
の形が異なるのはなぜか?
2) ![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) の積分範囲は1つの独立変数のものだが,もう片方の扱いは?
3)端点を固定しているという境界条件だけでは,
の積分範囲は1つの独立変数のものだが,もう片方の扱いは?
3)端点を固定しているという境界条件だけでは, ![[\ ]](http://hooktail.maxwell.jp/bbslog/7541b1af090dec7db3eb1953f2b90cc1.png) を0にするには無理がないか?
を0にするには無理がないか?
ということになります.
ご教示のほど,よろしくお願いいたします.m(_ _)m
Re: 変形オイラーの方程式における重積分の扱いについて
YAS_YAS さんのレス (2009/07/12(Sun) 15:32)
スイマセン,YAS_YASですが,
はじめてなもので,文章のあちこちが間違えている上に, パスワードを設定し忘れて,削除も出来ない状態になってしまいました.
改めて投稿したいと思います.
管理人様へ お手数ですが,本記事を削除して頂けるとありがたいです.
以上,よろしくお願いいたします.