汎関数微分
汎関数微分
トビラ.. さんの書込 (2009/07/11(Sat) 23:33)
こんばんは,
答えがどこにも載っていないのでお聞きしたいのですが, 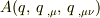 の
の  による汎関数微分を僕が計算すると
(ここで,
による汎関数微分を僕が計算すると
(ここで, 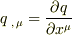 定義しました.)
定義しました.)
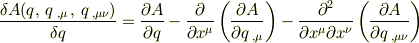
となるんですが,この結果は正しいのでしょうか?
変分 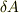 を考えると,この式の右辺第3項はプラスになる気もしますが,そのあたりのことがよくわかりません.
どうか,教えてください.お願いします.
を考えると,この式の右辺第3項はプラスになる気もしますが,そのあたりのことがよくわかりません.
どうか,教えてください.お願いします.
Re: 汎関数微分
mNeji さんのレス (2009/07/12(Sun) 00:27)
当てずっぽうモードですが,変分 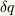 は「微量な関数」であって,「微分」ではないのが味噌だと思います.従って,恐らく;
は「微量な関数」であって,「微分」ではないのが味噌だと思います.従って,恐らく;
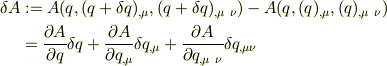
でしょうが,先ず右辺の第2項に着目すると,
![\frac{\partial A}{\partial q_{,\mu}}\delta q_{,\mu}&= \frac{\partial A}{\partial q_{,\mu}}\frac{\partial \delta q}{\partial x_{\mu}}\\&= \frac{\partial }{\partial x_{\mu}}\left[ \frac{\partial A}{\partial q_{,\mu}} \delta q \right] -\frac{\partial^2 A}{\partial x_{\mu}\ \partial q_{,\mu}}\delta q](http://hooktail.maxwell.jp/bbslog/8a84f96974fc66879edf49cc448e12fe.png)
となり,この右辺の第1項は積分時の境界条件で落ちるのでしょうね.
とすれば2階の偏微分項でも同じ事になるので,お説で良いような感触をもちます.
Re: 汎関数微分
トビラ.. さんのレス (2009/07/12(Sun) 01:08)
多分普通の変分を考えれば第3項はプラスになるんでしょうが,僕の持っている本では汎関数微分の定義が,
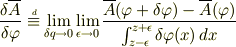
なんです.これで計算すると,僕は第3項がマイナスになってしまいました.
そのほかの計算でこの定義を用いても何の問題も起こらなかったのですが,どうなんでしょうか?
ちなみに, 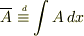 と定義し,離散近似で計算して答えを導き出します.
と定義し,離散近似で計算して答えを導き出します.
Re: 汎関数微分
トビラ.. さんのレス (2009/07/12(Sun) 02:12)
すみません!とけました!! 僕の勘違いでした. はぁーmNjiさんには迷惑かけたな・・・ 今度からもっと落ち着いて計算します..トホホ
Re: 汎関数微分
トビラ.. さんのレス (2009/07/12(Sun) 02:13)
ちなみに第三項はプラスになりました.
Re: 汎関数微分
トビラ.. さんのレス (2009/07/12(Sun) 03:08)
離散近似を用いて計算するんですが,
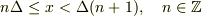 として,近似的に
として,近似的に 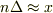 と置き,これにともなって
と置き,これにともなって 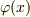 も近似的に
も近似的に 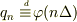 とします.これらは当然
とします.これらは当然 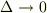 の極限で元の連続変数に戻ります.
また,この導関数も同様に次のように変化します.
の極限で元の連続変数に戻ります.
また,この導関数も同様に次のように変化します.
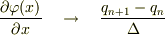
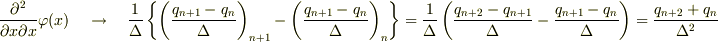 とこれが基本となる式なんですが,僕が間違っていたのはこの基本となる式の一番下の一番右の式において
とこれが基本となる式なんですが,僕が間違っていたのはこの基本となる式の一番下の一番右の式において
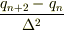 とプラスとマイナスを間違い,その後の計算が変になってしまいました.
この後も計算が続くのですが,少し長い計算で少しだけ面倒なのでmNejiさんや誰かの希望がない限り不本意ながらこの後の計算はやめておこうと思います.(笑)
それにしても,今日の踊る大捜査線ザムービー面白かったです.何回見ても面白いですね.あれは.ウヒョヒョヒョヒョ(笑)
とプラスとマイナスを間違い,その後の計算が変になってしまいました.
この後も計算が続くのですが,少し長い計算で少しだけ面倒なのでmNejiさんや誰かの希望がない限り不本意ながらこの後の計算はやめておこうと思います.(笑)
それにしても,今日の踊る大捜査線ザムービー面白かったです.何回見ても面白いですね.あれは.ウヒョヒョヒョヒョ(笑)
Re: 汎関数微分
トビラ.. さんのレス (2009/07/12(Sun) 03:23)
汎関数微分の定義っていろんな形みかけますけど,僕はここに載せた汎関数微分の定義が一番好きです. 一番尊敬する人(内山さん)の本に載っていたっていうだけの理由ですが.
Re: 汎関数微分
mNeji さんのレス (2009/07/12(Sun) 08:55)
>汎関数微分の定義っていろんな形みかけますけど,僕はここに載せた汎関数微分の定義が一番好きです. >一番尊敬する人(内山さん)の本に載っていたっていうだけの理由ですが.
なるほど,そちらの世界では「離散近似」という技法がメインなようですね.まだ当面,別の世界なので,門前の小僧モードで観戦しています(笑).
Re: 汎関数微分
toorisugari no Hiro さんのレス (2009/07/14(Tue) 10:56)
スルーしてたけど,
>
> とこれが基本となる式なんですが,僕が間違っていたのはこの基本となる式の一番下の一番右の式において
> 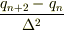 > とプラスとマイナスを間違い,その後の計算が変になってしまいました.
> とプラスとマイナスを間違い,その後の計算が変になってしまいました.
えっと,どちらも間違いで,
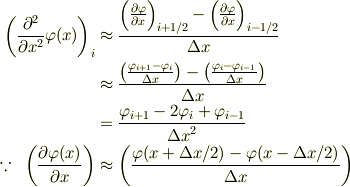
ですよね.
Re: 汎関数微分
トビラ.. さんのレス (2009/07/15(Wed) 03:57)
え?
そうなんですか?
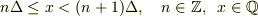 として近似的に
として近似的に 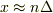 という定義を首尾一貫して使う限りは,僕のような計算になるんだと思うんですが,どうなんでしょうか.
もし,この定義が
という定義を首尾一貫して使う限りは,僕のような計算になるんだと思うんですが,どうなんでしょうか.
もし,この定義が 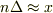 で厳密には
で厳密には 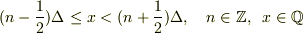 と,点
と,点 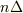 を
を 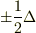 で囲うように範囲が定義されていたなら,toorisugari no hiroさんのような式になると思いますが,今回はそのような定義ではないため,違うと思います.例えば,
で囲うように範囲が定義されていたなら,toorisugari no hiroさんのような式になると思いますが,今回はそのような定義ではないため,違うと思います.例えば, 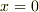 の場合,今僕の使っている定義だと
の場合,今僕の使っている定義だと 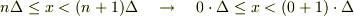 となるため,その
となるため,その  の範囲が
の範囲が 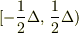 ではなく
ではなく 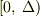 となると思います.
ちなみにtoorisugari no Hiroさんは
となると思います.
ちなみにtoorisugari no Hiroさんは 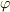 の
の  による微分の離散近似は
による微分の離散近似は
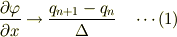
と考えているのでしょか?もしそうなら,新たに
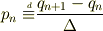
と定義して,上述の 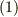 式の
式の 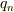 に,この
に,この 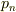 を代入すればそれは,
を代入すればそれは, 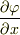 の微分,つまり
の微分,つまり 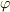 の2階微分ということになって僕の式が導けると思います.
の2階微分ということになって僕の式が導けると思います.
(ってか,関係ない話ですが,今日はご存知の通り僕の誕生日です!!(しるかっ!!) で,なんとか今日中に何年もかけて読んでいた内山龍雄さんの一般相対性理論の本が最後までたどり着きそうです.(やったー(笑)) なので明日からtoorisugari no hiro さんやmNejiさんの勧めてくれた本で量子論勉強します.)
Re: 汎関数微分
mNeji さんのレス (2009/07/15(Wed) 08:10)
トビラ..さん,
>(ってか,関係ない話ですが,今日はご存知の通り僕の誕生日です!!(しるかっ!!)
若い頃は,「誕生日なんて特別な意味が在るの?」と思っていましたが,いつ死んでも良い歳になると,健やかに居られるだけで有難いものだと感じるようになりました.
あまり夜更かしをしないように,たまには運動もして下さい.
>で,なんとか今日中に何年もかけて読んでいた内山龍雄さんの一般相対性理論の本が最後までたどり着きそうです.(やったー(笑))
その上,これは慶事ですね,二重にお目出度いです.トビラ..流の解釈論を拝見する楽しみが増えそうですね.
Re: 汎関数微分
トビラ.. さんのレス (2009/07/15(Wed) 14:14)
>あまり夜更かしをしないように,たまには運動もして下さい.
通勤時に全速で走っているので運動は多分大丈夫です.夜更かしは気をつけますです.
>トビラ..流の解釈論を拝見する楽しみが増えそうですね.
mNejiさんにそう言っていただけてすごくうれしいです.最高の誕生日プレゼントです.ありがとうございます.
Re: 汎関数微分
toorisugari no Hiro さんのレス (2009/07/15(Wed) 14:29)
> 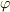 の2階微分ということになって僕の式が導けると思います.
>
の2階微分ということになって僕の式が導けると思います.
>
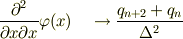
?
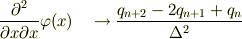
なら,nが一個分ずれてるが,まだ分かる...
Re: 汎関数微分
トビラ.. さんのレス (2009/07/15(Wed) 21:08)
ガーン まさにその通りです.僕の計算ミスでした. 最近この手の計算ミスが多いです. 今らかランドセル買ってきて来年の小学校の入学式の準備でもします.(0からやりなおそ・・・)
Re: 汎関数微分
toorisugari no Hiro さんのレス (2009/07/15(Wed) 21:57)
この手の計算をするときにはテーラー展開
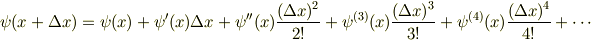
を使って誤差
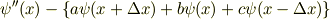
の値がもっとも小さくなるような( 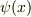 ,
, 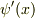 ,
, 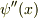 の項の係数が0になるような)
の項の係数が0になるような) 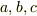 を選ぶのが,標準的な方法です.
ちなみに
を選ぶのが,標準的な方法です.
ちなみに
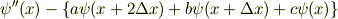
で計算しても,似たような式が出ますが,誤差は上の式より大きくなります.