行列

行列

pink さんの書込 (2009/07/11(Sat) 00:08)

以下の問題の流れを教えてもらえませんか？

問題：二次形式 t xAxの標準形を求めよ．ここに，x=(x) , t x=(x,y,z) (y) (z)

である．

私は，大学生なのですが，高校レベルの行列の知識程度です． この問題の流れ，ポイントを教えてください．．．

Re: 行列

pink さんのレス (2009/07/11(Sat) 00:09)

問題：二次形式 t xAxの標準形を求めよ．ここに，x=(x) , t x=(x,y,z)(y) (z)

である．

Re: 行列

transfer さんのレス (2009/07/11(Sat) 07:51)

x = (x, y, z) はベクトルで，tx はその転置のはずですが，真ん中の対称行列 A の固有値を求めて，それに対応する単位固有ベクトルを並べたものを T という行列とすると，x = T y などと置けば，標準形になります．（ここで y は新たなベクトル y = (ξ, η, ζ)） このとき，tx = ty tT のように，転置では y と T の順番が入れ替わります．（x = T y に対して） 詳しくは線型代数のテキストを見れば，例題で解き方もわかるはずです．

Re: 行列

toorisugari no Hiro さんのレス (2009/07/11(Sat) 14:45)

> 二次形式 t xAxの標準形を求めよ．

問題は3次元ですが，2次元で考えます． 行列 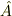\hat A に対する二次形式は

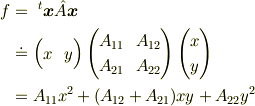
f &=~^t\bm{x}\hat A \bm{x}\\ &\doteq \begin{pmatrix}x & y\end{pmatrix} \begin{pmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{pmatrix}\begin{pmatrix}x \\ y\end{pmatrix}\\&= A_{11}x^2 + (A_{12}+A_{21})xy + A_{22}y^2

という 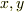x,y の2次式になります．

標準形を求めよとは，cross termを含まない形式

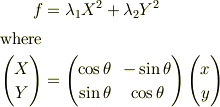
f &= \lambda_1 X^2 + \lambda_2 Y^2\\\text{where}\\\begin{pmatrix}X \\ Y\end{pmatrix} &= \begin{pmatrix} \cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{pmatrix}\begin{pmatrix}x \\ y \end{pmatrix}

となるような \lambda_1, \lambda_2, \theta を見つけよということです．

下の式を展開して上の式と較べることで，計算の末，

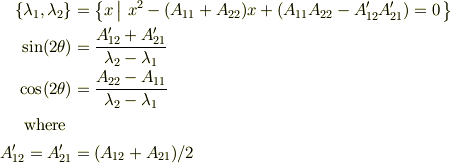
\{\lambda_1,\lambda_2 \}&=\left\{x \left|~ x^2 - (A_{11}+A_{22}) x + (A_{11}A_{22}-A'_{12}A'_{21}) = 0 \right.\right\}\\\sin(2\theta) &= \frac{A'_{12}+A'_{21}}{\lambda_2-\lambda_1}\\\cos(2\theta) &= \frac{A_{22} -A_{11} }{\lambda_2-\lambda_1}\\\text{where~}\\A'_{12} = A'_{21} &= (A_{12}+A_{21})/2

という式が得られます．

2次元でも結構やっかいなので，3次元の場合，体系立っていない方法では無理があります．transferさんのおっしゃるとおり，線形代数の本で「二次形式，対称行列，固有値・固有ベクトル」を勉強される事を勧めます．