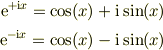複素インピーダンスの算出

AZM さんの書込 (2009/07/10(Fri) 15:49)

突然の質問で恐縮ですが教えてください．

Φ(t)=Φocos(ωt+α) をオイラーの公式を利用して， Φ(t)=Φoexp{i(ωt+α)｝と導出出来るはずなのですが，どうやってるのですか？オイラー以外に使っていますか？

> Φ(t)=Φoexp{i(ωt+α)｝と導出出来るはずなのですが，

できないと思います．

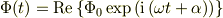
$\Phi(t) &= \mathrm{Re}\left\{ \Phi_0 \exp\left( \mathrm{i\,}(\omega t+\alpha) \right) \right\}$

なら分かりますが．

問題の文脈が分からないとこれ以上は何も言えません．

＞をオイラーの公式を利用して，

で実際に書き下すと，

$\mathrm{e}^{+\mathrm{i}x} = \cos(x) +\mathrm{i}\sin(x)\\\mathrm{e}^{-\mathrm{i}x} = \cos(x) -\mathrm{i}\sin(x)$

ですよね．辺々を加えると如何ですか？

他の教科書を進めていったら，理解できました．わざわざすみませんでした．ありがとうございました．

あっ！AZM＝数学迷い人です．すみません．学校でアクセスした時に，名前を適当に入れてしまいました．今後，気をつけます．すみませんでした．