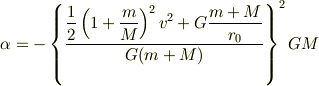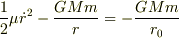ボーリングの玉とパチンコの玉,どちらの方が落ちるのが早い?
ボーリングの玉とパチンコの玉,どちらの方が落ちるのが早い?
大阪 さんの書込 (2009/07/08(Wed) 23:33)
ガリレオの実験です. ボーリングの玉とパチンコの玉,真空中で落下させた場合,どちらの方が早く落下するでしょうか? 答えはボーリングの玉です. 理由は, ボーリングの玉が起こす重力の方がパチンコの玉が起こす重力より大きいため,地球を引き寄せる力が大きい. 地球の動きは非常に小さいが質量が膨大なため,地球が動くと,運動量保存の法則により,ボーリングの玉の速度は大幅にアップする.
ということです. ここまでは,真実ですがちょっとひねくれた答えです.
ここからが疑問に思った質問となるのでよろしくお願いします. ボーリングの玉は重力場を生み出しています. ここまではもちろん納得しています. その重力場によって地球が動く. 非常に小さな動きだと思いますが,ここまでも納得しています. しかし,ボーリングの玉が生み出した重力場によって動いた地球の反作用で,なぜボーリングの玉の速度がアップしなければいけないのでしょうか. 地球が動いたからといって,直接ボーリングの玉と地球がつながっているわけでもなく,地球から重力以外の力を受けるわけでもないのに,ボーリングの玉の速度がアップする理由がわかりません. 地球が動くことによって,ボーリングの玉にはどのような力が働いたのでしょうか. スッキリする回答をおねがいします.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/09(Thu) 00:30)
>地球の動きは非常に小さいが質量が膨大なため,地球が動くと,運動量保存の法則により,ボーリングの玉の速度は大幅にアップする.
??これいいかえると,ボーリングの玉の速度が大幅にアップしないから(パチンコのたまと見分けがつかないくらい同じ速度で落ちるから),運動量保存則により,ボーリングの玉の重力では,地球はほぼ微動だにしないと言えるんじゃない?
>地球が動いたからといって,直接ボーリングの玉と地球がつながっているわけでもなく,地球から重力以外の力を受けるわけでもないのに,ボーリングの玉の速度がアップする理由がわかりません.
地球が近付けばそれだけ地球の重力が強くなるので,加速力がアップするのではないでしょうか?
運動量保存則があるから動くんじゃなく重力で動き,その結果運動量保存則が守られているんじゃないでしょうか?.
つまりは,ボーリングの重力で地球が動いたから,運動量保存則により,ボーリングが加速するのではなく, ボーリングの重力で地球が動き(この地球の運動量をP),地球の重力でボーリングが動き(このボーリングの運動量をp),結果として運動量が保存されている. んだと思います. 例えば初期の地球とボーリングの運動量がわかっていたとします.で,上述よりPも解っているとします.よって運動量保存則よりpが求まります.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/09(Thu) 06:58)
大阪さん,トビラ..さん,こんにちは.なかなかおもしろい議論だと思いました.
地球とボーリング球の質量を 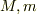 とすると,相対距離
とすると,相対距離  に対して,運動方程式
に対して,運動方程式
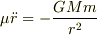
が成立します.ここで 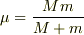 は,換算質量です.すると,
は,換算質量です.すると,
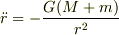
となりますから,両者が近づく加速度は質量  が大きいほど大きくなる結果になるということですね?
が大きいほど大きくなる結果になるということですね?
ただし,ボーリングの玉がもともと地球の一部であったということからすると,質量の合計  はもともとの地球全体の質量ですから,ボーリングの玉がどんなに重くともそれがもともと地球の一部であることに変わりがなければ,落ちる速さはまったく同じという結果になると思います.
はもともとの地球全体の質量ですから,ボーリングの玉がどんなに重くともそれがもともと地球の一部であることに変わりがなければ,落ちる速さはまったく同じという結果になると思います.
大阪さん,ボーリング玉がより重くなったことによって,より速くなるのは実は地球の方です.地球とボーリング玉の座標を 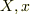 ,その加速度を
,その加速度を 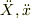 とすると,両者の運動方程式は
とすると,両者の運動方程式は
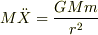 すなわち,
すなわち, 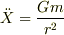
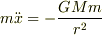 すなわち,
すなわち, 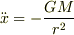
ボーリング玉の方は,地球の質量のみによって加速度が決まり,地球の方はボーリング玉の質量のみによって加速度が決まることになります. 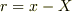 を考慮して上の
を考慮して上の  に対する運動方程式を得ます.私たちが関心をもっているのは「どちらが速く落ちるか」ですから,両者が近づく速さを比べることになります.すると上のように近づく加速度は
に対する運動方程式を得ます.私たちが関心をもっているのは「どちらが速く落ちるか」ですから,両者が近づく速さを比べることになります.すると上のように近づく加速度は  に比例することになるわけです.
に比例することになるわけです.
もし,質量の異なる2つの球を一緒に落としたらどうなるでしょうか?ただし,両者の間の万有引力は無視しましょう.
質量 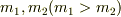 とすると,2つの球の加速度は質量にかかわらず同じ.一方地球の加速度は
とすると,2つの球の加速度は質量にかかわらず同じ.一方地球の加速度は 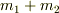 に比例することになります.したがってこの場合は2つは同時に落下することになるでしょう.
に比例することになります.したがってこの場合は2つは同時に落下することになるでしょう.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
大阪 さんのレス (2009/07/09(Thu) 11:54)
ごめんなさい,あまりいい例文じゃなかったので,例文を変更させて下さい.
人工衛星が遠くの星に行くときに, 飛び立った速さのみで飛行すると,時間がかかりすぎてしまうため, スイングバイという方法で加速します. 木星や土星に近づいて,その時に得た速度で飛んでいくというものです. しかし,奇妙だと思いませんか? 位置エネルギーを運動エネルギーに転換したのならば, 同じ位置に戻ったときには運動エネルギーは戻ってしまうから加速はしないはずです. しかし,実際は加速しており,原因は星の運動エネルギーを人工衛星に移したためです. 式で書くと, MV+mv=MV'+mv' で,V→V'とv→v'は逆方向の増加です. 星の速度の変化は微々たるものですが,Mが大きいためvの変化が大きくなります.
この式の意味は分かりますし,納得もしています. しかし,星と人工衛星は直接つながってはいないのに, 星の動きの変化によってなぜ人工衛星の動きが変化するのでしょうか.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/09(Thu) 13:24)
>しかし,星と人工衛星は直接つながってはいないのに, >星の動きの変化によってなぜ人工衛星の動きが変化するのでしょうか.
もちろん,引力を及ぼし合っているからですよね.
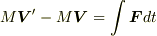
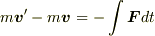
相互に及ぼし合う引力 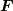 と
と 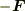 が作用・反作用となって,その力積によって相互に運動量を交換したわけです.
相互に受ける力(または力積)が同じ大きさなのに質量が異なるために,速度変化が質量に反比例した大きさで生じるということですよね?
が作用・反作用となって,その力積によって相互に運動量を交換したわけです.
相互に受ける力(または力積)が同じ大きさなのに質量が異なるために,速度変化が質量に反比例した大きさで生じるということですよね?
それとも,遠隔相互作用がありえないとされるもとで近接相互作用としての重力の解釈を求められているのかな?
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
toorisugari no Hiro さんのレス (2009/07/09(Thu) 17:28)
>>しかし,星と人工衛星は直接つながってはいないのに, >>星の動きの変化によってなぜ人工衛星の動きが変化するのでしょうか.
> それとも,遠隔相互作用がありえないとされるもとで近接相互作用としての重力の解釈を求められているのかな?
たぶん,「作用反作用則は,接触時に発生する力(接触力)に対してのみ成り立つ.」と思われているからではないでしょうかね.
# 作用反作用則は接触力の現象論から導かれたのでprimitiveには接触力限定ですが,現代物理では違います.「運動量保存則から作用反作用則が導ける」ので,運動量保存則の保証の元,近接・遠隔関係なく,どの力でも作用反作用則は成り立つと考えてますよね.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
大阪 さんのレス (2009/07/09(Thu) 19:10)
ありがとうございます.
自分でも何がわからないのかわかってきました. 大雑把に言うと,今回に関して,作用-反作用の力とは具体的には何なのかわかりません. もうちょっと具体的に言うと, 星が重力場を作り出し,その重力場に沿って人工衛星が運動しているだけなのに, 重力場を作り出してる星が動くとなんで人工衛星が影響を受けるのかがわかりません. 重力が強くなったわけでもなく,電磁気力や強い力,弱い力のいづれも働いたわけでもないのに, 人工衛星が加速するための力がなんなのかわかりません. って最初の質問時に言えばよかったのですね… 話がまとまっておらず,申し訳ありません.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
toorisugari no Hiro さんのレス (2009/07/09(Thu) 19:58)
> 星が重力場を作り出し,その重力場に沿って人工衛星が運動しているだけなのに,重力場を作り出してる星が動くとなんで人工衛星が影響を受けるのかがわかりません.
「第三者が星を動かして,それによって(間接的に)人工衛星が影響を受ける.」という話ではありません.
> 運動しているだけなのに
人工衛星もしっかり星に影響を与えていることをお忘れなく.
> 重力が強くなったわけでもなく,
いや,その既存の重力で十分です.
「重力場を作り出してる星が動く」原因となる力は星が人工衛星に及ぼす重力の反作用,つまり,人工衛星が星に及ぼす重力です.当然その反作用(=星が人工衛星に及ぼす重力)で人工衛星の運動量は変化します. # つまり,星の運動量が変化すれば,孤立系の片割れである人工衛星の運動量も打ち消すように変化する.and vice versa.こうして,孤立系の全運動量は保存される. # 何故,作用反作用則が成り立つのか?それは運動量保存則が成り立つから.何故,運動量保存則が成り立つのか?それは世界が並進不変性をもつから.何故,世界は並進不変性をもつのか?単純で美しいから.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/09(Thu) 21:37)
>何故,世界は並進不変性をもつのか?単純で美しいから.
なぜ世界は単純で美しいのか?Homo Sapience がそう認識するように進化したから…かな?
運動量保存は,力=相互作用を及ぼしあう両者が系に含まれる限りにおいて,そして他の外力が無視できる場合にはいつでも成り立つのですよね.たとえば,私たちは歩き始めるときに地球をけって地球に運動量を与えることで逆向きの運動量を自らに獲得している.ただし,地球の質量があまりに大きいのでその運動量変化は測定不能なわけです.もちろん,私が歩き始めたことが地球の運動に影響しているとはいいにくい.でも,理論上はそうでなければならないという確信が私たちにはあるわけです.
そして,このとき運動量交換の原因たる力は摩擦力という接触力で,私は地球から摩擦力によって前に押され,地球は私から摩擦力によって後ろに押される.これが作用-反作用ということになります.遠隔力たる重力もまさに相互作用なのだから,人工衛星が星から引かれるときに星は人工衛星から逆向きで等しい力で引かれる.これが相互の運動量交換の原因ということができるわけですね.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
大阪 さんのレス (2009/07/10(Fri) 01:17)
>「第三者が星を動かして,それによって(間接的に)人工衛星が影響を受ける.」という話ではありません. 了解しています.言い回しがよくありませんでしたね.ごめんなさい.
>人工衛星もしっかり星に影響を与えていることをお忘れなく. 了解しています.言葉足らずで申し訳ありません.
>いや,その既存の重力で十分です. 既存の重力だけでは,一時的に加速したとしても加速前の位置に戻ると運動エネルギーが位置エネルギーに戻されて再び同じ速度に戻ってしまうのではないでしょうか.
>人工衛星が星から引かれるときに星は人工衛星から逆向きで等しい力で引かれる. これはニュートン力学の概念で, 言い回しが違うだけかもしれませんが,お互いはお互いが作り出す重力場を自然な運動しているだけだと思います. 明確に引き寄せるということはなく,歪んだ空間に対して最短距離をまっすぐ進んでいるだけだと思います.
作用反作用自体は何の疑問も思っていません. 人工衛星はどうして星の運動量が変化したことを知り得るのかが疑問です. 人工衛星と星をつなぐのは重力だけですが,星の速度変化が微々たるものなので,重力の変化もほとんどないと考えています.
星が動くときに人工衛星を引っ張った(人工衛星を引っ張ることにより星が動いた)のであればわかりますが, 星も人工衛星もお互いの作り出した重力場に沿って自然な運動をしているだけなのに, 重力場を作り出している本人にどうやって影響(運動量の変化の通知)を与えたのかが疑問です. 星と人工衛星の間に力や運動量の変化を伝えたものはなんでしょうか.
加速するからには何かの力が働いたのは必至だと思っており, 電磁気力,強い力,弱い力は今回関係ないので, 重力なのかもとは思っていますが,今回,重力の変化は小さすぎます. でも重力以外考えられないし・・・ 小さくても人工衛星を加速させるためには十分な変化量なのか・・・ と悩んでいます.
ちなみに,Javaで星の運動のプログラムを作成してみました. (組み込んだのはニュートンの重力力学程度.作用反作用は組み込んでいません.) みごとにスイングバイが起こっていました(笑) 雑なプログラムなので今回の話題とは無関係かもしれませんが・・・ やはり重力が運動量の変化を伝えたのか・・・ それとも運動量という概念はなく,お互いの速度変化が自然と発生し, 運動量として計算するとそれがきれいに釣り合うということだけなのか・・・ なんとも言えないような宙ぶらりんな気持ちで彷徨っています. きっと,微々たる重力の変化が人工衛星を加速させているんでしょうね. という結論に至りました.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/10(Fri) 02:52)
ちょっと話変わるんですけど,すみません,僕も疑問に思ったことがあるので聞いてくださるとたすかります. 僕は質量の大きい物体の方が,大きく加速する様な気がするんですが,どうなんでしょう?というのも,質量が大きいものほどそれだけ地球をひきつけるからひきつけた分だけ,地球との距離も縮まりそれだけ強い重力を受けるので軽い物体より加速する気がします.もちろん地上で同時に落としても意味ないので,別々に落とす場合の話ですが.例えボーリングの玉を落としても,その違いは観測できないでしょうが理論上は違う気がします.
そこで,方程式をたててこの考えについて検証してみたいんですけど,うまくできませんでした.なのでこの式のどこが間違っているのかアドバイスお願いします.,
まず,簡単のため1次元を考えることにします.初期条件として地球を座標原点に,ボーリングの玉の座標を  軸上の負の無限遠方に設置します.また,これらは初速度0とします.また,地球は回転していないものとしNewton力学(スペル合ってる?)の範囲で計算するとします.
記号としては,地球の原点からの距離を
軸上の負の無限遠方に設置します.また,これらは初速度0とします.また,地球は回転していないものとしNewton力学(スペル合ってる?)の範囲で計算するとします.
記号としては,地球の原点からの距離を 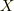 ,地球の質量を
,地球の質量を  ,地球の速度を
,地球の速度を  とし,この記号のそれぞれ対応するアルファベットの小文字をボーリングの玉の記号として採用します.例えば,ボーリングの玉の質量は
とし,この記号のそれぞれ対応するアルファベットの小文字をボーリングの玉の記号として採用します.例えば,ボーリングの玉の質量は  などです.また,ボーリングの玉の加速度を
などです.また,ボーリングの玉の加速度を  ,ボーリングの玉と地球との距離を
,ボーリングの玉と地球との距離を  とします.
ここでの目的はボーリングの加速度
とします.
ここでの目的はボーリングの加速度  を
を 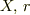 やこの時間に関する導関数を使わずにあらわすことが目的です.よって,ボーリングの玉の加速度とボーリングの玉の質量の関係式を導き出すのが目的です.
まず,基本となる式を書き出すと.
やこの時間に関する導関数を使わずにあらわすことが目的です.よって,ボーリングの玉の加速度とボーリングの玉の質量の関係式を導き出すのが目的です.
まず,基本となる式を書き出すと.
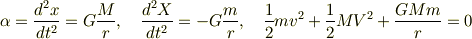
となります.それぞれ,一番左の式を第1式,真ん中の式を第2式,右の式を第3式と呼ぶことにします. 第1と第2は万有引力の方程式(?)です.で,第3式は自信ないですが,エネルギー保存から導いた式です. まず第1式と第2式を合わせて
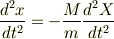
この式を  で積分すると
で積分すると
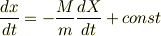
初期条件により 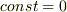 となります.この式を変形して
となります.この式を変形して
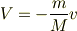
となって,この式を第三式の第2項に代入し,第一式から, 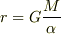 となるので,これを第3式の第3項の
となるので,これを第3式の第3項の  に代入すると
に代入すると
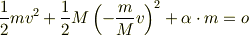
となり,これを変形すると
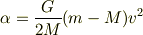
となります.
というか,これであっているのでしょうか?ぱっと見おかしいですよね?この方程式.
こういう感じの式を作って質点の,加速度と質量の関係を与えたかったんです.例えば,質量 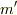 パチンコの玉のが速度
パチンコの玉のが速度  のときと,ボーリングの玉(質量
のときと,ボーリングの玉(質量  (
( 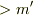 ))の速度も同じく
))の速度も同じく  のときとではボーリングの玉の加速度の方が大きいことになるって言いたかったんですけど,この式やっぱおかしいですよね.だって,
のときとではボーリングの玉の加速度の方が大きいことになるって言いたかったんですけど,この式やっぱおかしいですよね.だって, 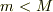 だから減速しているし.なぜ?どこで間違えたんでしょう?
やっぱエネルギー保存則で立てた式第3式でしょうか?とくに位置エネルギーについてメッチャ自信ないです.
だから減速しているし.なぜ?どこで間違えたんでしょう?
やっぱエネルギー保存則で立てた式第3式でしょうか?とくに位置エネルギーについてメッチャ自信ないです.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
ヒノッキー さんのレス (2009/07/10(Fri) 04:44)
横から失礼します. トビラ..さんの論議とはズレますが, スイングバイという単語に興味があったので, 少し調べてみました.
大阪さんのおっしゃった,
>きっと,微々たる重力の変化が人工衛星を加速させているんでしょうね.
ですが,これが微々たる重力の変化でなければどうでしょうか? (つまり,宇宙のスケールを見誤っているとしたら?)
地球の話ですが,wikiから, 地球の平均軌道速度は29.7859 km/sであるとありました. 我々は地球の表面から100km以内のとこで暮らしていて, このくらいの重力の変化は無視できるとして考えられていますが, この平均軌道速度は,4秒以下で地上から大気圏を突破できるくらいの 速度です. ・・・スイングバイしている時間で,惑星の重力場が 著しく変化するのなら,運動量の変化もともに著しいものになります. (一時間のスイングバイを行うと,その間に地球は 29.7×3600km動くことになる!)
・・・正直,こんなに速く地球が動いてることにびっくりです.
それとトビラ..さんの論議ですが,
>質量が大きいものほどそれだけ地球をひきつけるからひきつけた分だけ,地球との距離も縮まりそれだけ強い重力を受けるので軽い物体より加速する気がします.
ひきつける力は大きくなりますが, 物体は質量の大きいものほど動きにくい,ということの考慮を 忘れているような気がします.
・・・式はあまり見てないので, 間違ってたらすみませn.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/10(Fri) 05:25)
>重力場を作り出している本人にどうやって影響(運動量の変化の通知)を与えたのかが疑問です.星と人工衛星の間に力や運動量の変化を伝えたものはなんでしょうか.
その正体がメール便ではないことは確かなようだね.例えば,星の重力の影響を受ける前と後では,衛星の運動状態(運動量)が変わっているから,運動状態が変わっているということは,衛星が星に放った重力が星のどのあたりに当たるのか,や,衛星の重力の強さが,前と後とで変わっているから,その違いをそろばんやでんたくで星が計算すると,自分(地球)の重力を衛星がどのくらい受けたかって理解するんじゃない?ただ,自分の運動量が変わったんですって伝える必要あるの?この人たち意識ないんだし,例え意識あったとしても,それを知ったからってどうなるものでもないんじゃないの?動く原因は力が加わる以外ないとおもうし.
>人工衛星はどうして星の運動量が変化したことを知り得るのかが疑問です.
それとも,遠隔作用が疑問なの?そもそもすべての力は遠隔作用とも解釈できるよ?例えば,手でものをつかんで持ち上げても,そのものと手とがミクロの世界では直接触れているわけではなく.電弱力だっけ?なんかそういった力が働いているから,触れているといってもごくわずかな隙間がある.だから,運動量の問題は今回に限ったものではないと思う.
ただ,場の理論によるとそれら遠隔作用を近接作用に昇格させることができる.つまり,粒子と粒子の間に働いていた遠隔作用が,「場」と粒子の近接作用になる.(って本で読んだ気がする) もっというなら,場の量子化を考えればいいと思います.つまり,重力子と物質との相互作用です. 今回は人工衛星を一つの粒子と考えます.すると,この粒子に星から重力子が飛んできて,粒子の軌道が曲がります(つまり,運動量が変化する).同時にこの粒子は星にも向けて重力子を放ちます.この重力子が星に当たれば当然星の軌道や速度,つまり運動量が変わります.って遠隔作用を近接作用に昇格させて考えるのもなんか納得いかない?もっと平たく言うと,粒子が重力子を放った時運動量は保存されててその重力子と星とがぶつかり,そこでも星と重力子との運動量が保存されてる・・・つまり,運動量保存がどこにでも成り立っている.とはいっても,僕場の理論知らないから今言ったことすべて間違っているかも.ごめんね.ここまで読ませといて,今さら
ってかもしかして僕が質問の意味をはきちがえてるの?
というか,質問が難しくて質問の意味をあまり僕が理解していないのかも.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/10(Fri) 05:32)
>物体は質量の大きいものほど動きにくい,ということの考慮をいれると
同じ重力場だと,等価原理よりどんな受動的重力質量をもっていようと落下速度は同じだよ.
僕が言いたかった質問は,落下速度の問題じゃなく,互いの物体が初速度0になるようなミンコフスキー型の座標系をもうけ,その座標系に対しての質点の「加速度」を知りたかったんだよ.だから,落下速度や相対速度の問題ではないんだよ.
ん?だから,質量がおきいものほどっていう考えを採用しなくてはならないのかな?ん??ん??? だけど,あの式のどこが間違っているか気になる.間違っているのは確かだろうけど,どこだかわからない.誰か教えてちょ
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
toorisugari no Hiro さんのレス (2009/07/10(Fri) 09:02)
> 既存の重力だけでは,一時的に加速したとしても加速前の位置に戻ると運動エネルギーが位置エネルギーに戻されて再び同じ速度に戻ってしまうのではないでしょうか.
何が「加速前の位置に戻る」に戻る時でしょうか?人工衛星が星に対する「相対的」な位置関係だけでなく,星のたとえば遠方の星座群および太陽に対する「絶対的」な位置関係も含めていますか?
同様に星のたとえば遠方の星座群および太陽に対する「絶対的」な速度も考えていますか?
それらも含めて元に戻るなら,当然「同じ速度に戻ってしまう」のは当たり前ですが,反論にはなりません.
# 最初から「既存の重力だけでは」という思いこみが強く働いているように思います.
重力場は存在せず,星と衛星が見えないゴム紐 ( いくらでも延びる.常に弛まない.質量ない.切れない. ある距離以上離れると張力は減少し始め,十分遠方では張力は0. ) でつながれている場合もスィングバイは起きますが,そのときも納得はできないのでしょうか
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
toorisugari no Hiro さんのレス (2009/07/10(Fri) 09:26)
スィングバイって,計算が複雑だから不思議に思えるかもしれませんが, 本質的には 「 非常に大質量の剛体球が一定の速さで走っている.そこに,小質量の剛体球が現れ,二つは弾性衝突した.衝突の角度によっては,小球ははじき飛ばされ速さは増加し,大球の速さは(微小ながら)減少することがあった. 」 と何ら変わりません.
運動量の交換が,瞬間的な斥力的接触力で行われるか,有限の時間での引力的な遠隔力で行われるか,の違いがあるに過ぎません.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
toorisugari no Hiro さんのレス (2009/07/10(Fri) 09:47)
>>何故,世界は並進不変性をもつのか?単純で美しいから. > なぜ世界は単純で美しいのか?Homo Sapience がそう認識するように進化したから…かな?
冗談に,一番適切な冗談で返していただいて感謝します.:-) by 隠れ「人間原理」主義者
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/10(Fri) 11:16)
トビラ..さん,No.24562で問題は解けていませんか?
大阪さん,人工衛星(ボーリング玉)の加速という現象が星(地球)の加速と数学的な関係で結ばれているからといって,直接的な因果関係をそこにみつける必要はないのではありませんか?だって,加速自体は重力のせいであり,またお望みであればそれは「時空の曲がり」のせいなのですから.瞬間における加速度は重力場の曲がり具合で決まるわけです.
もちろん,星(地球)の運動は重力場の形を変えますから,その影響は当然現れます.しかし,これはまた別の問題です.星(地球)がほとんど運動しないためにほとんど変わらない曲がった時空の測地線にそう運動すなわち加速運動が起こるのです.大阪さんの議論にはこの2つの混同が見られると思います.
重力源の運動による影響はもちろん重力波として伝播し,有限だけれどごく短い時間の後に人工衛星(ボーリング玉)の位置に伝わってきます.ゴム膜モデルがわかりやすいと思いますが,星(地球)の運動でゴム膜のへこみ具合が変わり,近くを運動する人工衛星(ボーリング玉)の運動にもちろん影響を与えるわけです.しかし,今回の運動量交換の話はこれとは異なる話です.
今回の問題について整理すると,星(地球)も人工衛星(ボーリング玉)もその質量によってゴム膜(時空)を変形させている.その変形のもとで両者は測地線に沿う「加速」運動をしているのです.人工衛星(ボーリング玉)の加速は,星の加速と(数学的に結ばれる関係にはあるけれども)直接の因果関係にはなく,その瞬間にあるゴム膜の曲がりで十分なのですよ.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
toorisugari no Hiro さんのレス (2009/07/10(Fri) 12:07)
そもそも大阪さんは
> 星の動きの変化によって
速度の変化(運動量の変化)と加速度の変化(重力場の変化)を混同しています.
今回の問題は,Yokkunさんもおっしゃるように,後者は関係ありません.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/10(Fri) 14:18)
yokkunさんへ yokkunさんのはyokkunさんので正しいのですが,僕が求めたいのは多分yokkunさんのと問題が違うと思います. yokkunさんが求めたのは相対速度による落下速度,や運動方程式. 僕が求めたいのは,2つの物体の初速度が0となるような,ミンコフスキー型の座標系に対して,落下している物体の加速度を,自分の座標(原点からの距離)だけで表したいというものです.ですから,相手の座標(原点からの距離)や,相手の物体との相対距離が現れてはだめなんです. そして,これはNewton力学の範囲で求めるとします.なので,このような方程式を考えることにより,Newton力学では,質量の重いほうが重力による加速度が大きいのでは?と思うということを示したかったんです. つまり,この座標系に対する加速度の導出です.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/10(Fri) 14:24)
>mv^2/2+MV^2/2-GMm/r=0
ミュフ猫さんありがとうございます.ということは僕の結果の式は
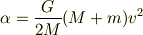
となるんでしょうか? あと,ほかにも単純な計算ミスしていたようで僕.ごめんなさい. この式だと僕の思考実験ともつじつま合います. つまりは,質量の重いほうが,この座標系に対して速く加速する.ってことになるんだと思います. というか,どの座標系においても質量の大きいほうが落下速度は速いかな.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/10(Fri) 16:10)
>2つの物体の初速度が0となるような,ミンコフスキー型の座標系に対して
質量中心系が最も簡便なそれに当たるような気もするのですが,違うのでしょうか?
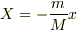 が常に成り立ちますから,
が常に成り立ちますから,
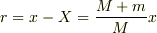 すると,
すると,
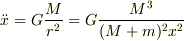 質量が大きい方が,質量中心系に対しては遅くなるという結果になっちゃいました.重心が
質量が大きい方が,質量中心系に対しては遅くなるという結果になっちゃいました.重心が  の方にずれるためでしょうかね?
の方にずれるためでしょうかね?
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/10(Fri) 16:24)
>質量中心系が最も簡便なそれに当たるような気もするのですが,違うのでしょうか?
それは,初期条件が異なってしまいます.つまり,質点の重心を座標原点におくってことですよね? そうすると,質量によって重心の位置が異なってくるので,質量によって初期条件が異なることにならないでしょうか? なので,質量に依存しない座標系を考える必要があると思います.
具体的に説明すると,初期条件として,お互いの初速度0とし,また,お互いの距離が  だとします.さらにその重心を座標原点にすると,質量が軽い場合はその重心が地球の近くに設けられますが,質量が重い場合はその重心が地球から離れてしまい,逆に重心の方に質点がよってしまいます.なので,質量の選び方によって,質点と座標原点との距離の初期条件に違いがうまれるため,質量と加速度の関係式を求めるにあたり,質量に寄らない座標系を設ける必要があると思いその座標系は用いませんでした.
だとします.さらにその重心を座標原点にすると,質量が軽い場合はその重心が地球の近くに設けられますが,質量が重い場合はその重心が地球から離れてしまい,逆に重心の方に質点がよってしまいます.なので,質量の選び方によって,質点と座標原点との距離の初期条件に違いがうまれるため,質量と加速度の関係式を求めるにあたり,質量に寄らない座標系を設ける必要があると思いその座標系は用いませんでした.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/10(Fri) 16:36)
>重心がの方にずれるためでしょうかね?
ごめんなさい,最後までちゃんと読んでませんでした.気づいていたんですね. そうだと思います.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/10(Fri) 16:53)
トビラ..さん,そういうことなんだと薄々感じましたが,やはりそうでしたか.
すると,問題の解決は不可能なような気がします. いずれの場合も「同じ」位置で加速度を比較したいのですよね(ちなみにトビラさんのNo.24594の結果は同じ速さのときでの比較になっています)?無限遠からの初速ゼロでの接近を考える場合は,「同じ」位置という定義は意味をなさないのではないでしょうか?絶対静止系を定義することになると思います.このとき私たちが知りうるのは等しい相対座標で比べた相対速度のみではないのかなあ?
有限の位置からの接近であれば,重心は静止していますから等しい時刻における加速度なり速さを比較することはもちろん可能だと思います.このときも等しい時刻での比較が等しい位置での比較にならないことはいうまでもありません.しかし,どちらが速いかということでは十分ですし,座標系の定義が初期位置に対して明確ですから同じ位置での比較もできますね?無限遠からの接近の場合は,重心は静止はしているのですがその位置を定義できません.また,接近には無限大の時間を要しますから同一時刻での比較も不可能です.唯一可能な選択は,重心で重なっていた両者が分裂して無限遠に離れ去る運動の逆を考えることです.これはもちろん質量中心系を選択することに他なりませんよね?
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/10(Fri) 17:36)
今からアルバイトなので,今は詳しく議論できませんが, 僕はNewton力学では,と書いてなかったですか?どこかに, なので,僕は相対論的な観測の問題を出しているわけではないです. 理論上はという意味ですし,初期条件を無限遠方にしたのは計算の簡単化のためで,具体的に有限距離で公式を導いても似たような結果になると思います.ただ式は複雑になるでしょうが, それではバイトに行ってきます.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/10(Fri) 19:27)
行ってらっしゃい.
>僕はNewton力学では,と書いてなかったですか?
もちろんです.Newton力学の範囲で考えています.
>初期条件を無限遠方にしたのは計算の簡単化のためで,具体的に有限距離で公式を導いても似たような結果になると思います.ただ式は複雑になるでしょうが,
なるほど.ようやく解ける問題になったようですね. 重心は静止したままなので,運動方程式は質量中心系と同じで重心の座標を質量条件によってずらせばOKですね.ちょっとおもしろい問題になりました.
[問題]
質量がそれぞれ 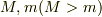 の2物体が初期位置
の2物体が初期位置 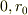 から初速ゼロで万有引力を及ぼし合いながら接近するときの運動を記述し,質量
から初速ゼロで万有引力を及ぼし合いながら接近するときの運動を記述し,質量  の変化によって運動がどう変化するか調べよ.
の変化によって運動がどう変化するか調べよ.
数値積分も可能ですから,考えてみようかな.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/10(Fri) 23:03)
>行ってらっしゃい
行ってきました.
>重心は静止したままなので,運動方程式は質量中心系と同じで重心の座標を質量条件によってずらせばOKですね.ちょっとおもしろい問題になりました
なるほど,柔軟な発想ができてうらやましいです.
>[問題]
合っているかどうかはわかりませんが,僕の計算では
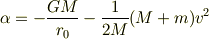
なりました.(  は質点
は質点  の加速度)
右辺がすべてマイナスなのは質点が原点より正の方向にあるため,です.例えば,この式の両辺に
の加速度)
右辺がすべてマイナスなのは質点が原点より正の方向にあるため,です.例えば,この式の両辺に  をかければ左辺は力になり,負の方向に重力が作用しているので,右辺はマイナスにならなくてはならないので,そのことからも理解できると思います.
をかければ左辺は力になり,負の方向に重力が作用しているので,右辺はマイナスにならなくてはならないので,そのことからも理解できると思います.
Yokkunさん僕の計算に付き合ってくれてありがとうございました.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
tokyo さんのレス (2009/07/11(Sat) 00:21)
>ガリレオの実験です. >ボーリングの玉とパチンコの玉,真空中で落下させた場合,どちらの方が早く落下するでしょうか? >答えはボーリングの玉です. >理由は, >ボーリングの玉が起こす重力の方がパチンコの玉が起こす重力より大きいため,地球を引き寄せる力が大きい. >地球の動きは非常に小さいが質量が膨大なため,地球が動くと,運動量保存の法則により,ボーリングの玉の速度は大幅にアップする.
>ということです. >ここまでは,真実ですがちょっとひねくれた答えです.
事実なんですか?
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/11(Sat) 08:03)
tokyoさん,こんにちは.
>事実なんですか?
実験的な検証は無理ですが,天体の運動において力学の法則は精密に成立していることが確認されていますから,まず間違いのない議論であると思います.通常の実験可能な質量の物体と落下距離では測定は全く不可能です.なにせ地球を動かすという話ですから….厳密に言うとリンゴが落下するときに地球もリンゴの方に落下するのです.それを考慮すると…という途方もない話です.
トビラ..さん,αの式で分母のr^2のところ(ミュフ猫さんの指摘されたところ)をrのままで計算されているようです.したがってまた,次元がおかしくなっています.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
tokyo さんのレス (2009/07/11(Sat) 10:49)
Yokkunさん,お返事ありがとうございます. それでは,ここの重い物が先に落ちる?というガリレオ・ガリレイの記事は正確ではないんですね.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/11(Sat) 12:01)
>ガリレオ・ガリレイの記事は正確ではないんですね.
いえいえ,ガリレイの同時落下は十分正しいといっていいでしょう. なにせ地球がリンゴの方に落ちる距離も速さもとてつもなく小さく空想的なものに等しいのですから.地球に月が落下する…という天体間の力と運動という規模になるとそれが無視できなくなるのです.人間は視点の大きさやタイムスケールの幅を大きく変えながら,より正しいといえる真理に少しずつ迫っていくのですね.ガリレオは間違いでニュートンは正しいとか,ニュートンは間違いでアインシュタインは正しいとかいうのは,理論の「守備範囲」とか真理追求の歴史性とかを無視した議論で,人間のつくった理論の「正しさ」は常に相対的なものだといっていいのだろうと思います.
地上の物体の落下に関する限り,ガリレオの理論はまったくもって正しいといえます.それを質量によって異なるなどといっている私たちは,ちょっとヘソマガリなので天体の運動と地上の落下運動の法則が根っこでつながっているのをもとに「知的」な遊びをしているわけです.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/11(Sat) 19:44)
一応導出の過程をのせておきます. 今回基本となる方程式は
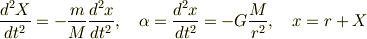
です. この式を左から順に第1式,第2式,第3式と呼ぶことにします. まず,第2式と第3式から
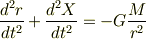
この式の左辺第2項に,第1式を代入して変形すると
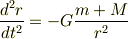
この式の両辺を 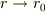 で積分して
で積分して
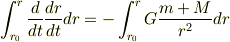
ここで, 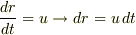 なので,この式の左辺は
なので,この式の左辺は
![\int^t_{t_0}\frac{du}{dt} u\,dt=\int^t_{t_0}\frac{d}{dt}\left( \frac{1}{2}u^2\right)dt=\left[ \frac{1}{2}u^2(t) \right]^t_{t_0}=\frac{1}{2}u^2](http://hooktail.maxwell.jp/bbslog/7caae2a8cdf310fc66f3dd88f7e9fde4.png)
ここで, 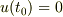 という初期条件を使った.
また,右辺は
という初期条件を使った.
また,右辺は
![\left[ G\frac{m+M}{r} \right]^r_{r_0}=G\frac{m+M}{r}-G\frac{m+M}{r_0}](http://hooktail.maxwell.jp/bbslog/35d7c0f6a038d5972de494684a81d7c5.png)
となる.したがって両辺をつなげると
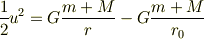
この式を第4式と呼ぶことにします.  を
を  を使った表示に戻す必要があるので,
を使った表示に戻す必要があるので,
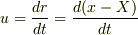 この式に第1式を用いて
この式に第1式を用いて
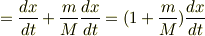
となる. この式を第5式と呼ぶことにする. また,第2式を変形すると

となるので,この式を第4式の右辺第1項に,第5式を第4式の左辺に代入して
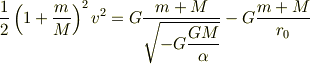
これを  について変形すると
について変形すると
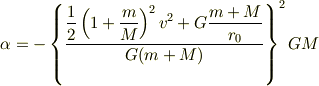
となります.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/11(Sat) 20:02)
そんな便利な式があったんですね. その式を導出するために,一から計算してしまいました.トホホ ちなみに,この式の次元式(?)は
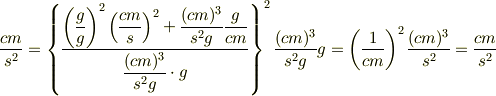
となって一致しますね. というか,今まで,次元を計算したことがなかったので,とても勉強になりました. なるほど,式があっているかどうかは次元を調べるのも一つの方法なんですね.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
トビラ.. さんのレス (2009/07/11(Sat) 20:31)
よく考えると,この式まだわかりずらいのでもう少し整理すると
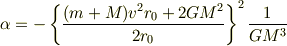
となって,  が大きいほど,この座標系に対する加速度が大きいことが,一目でわかる.
が大きいほど,この座標系に対する加速度が大きいことが,一目でわかる.
Re: ボーリングの玉とパチンコの玉,どちらの方が落ち
Yokkun さんのレス (2009/07/11(Sat) 20:50)
加速度は単調増加なので,同じ速さで比べた加速度が大きければ同じ時刻で比べた加速度も大きい…でいいのでしょうね.
ヒマがあったら,時間変化も追跡してみたいですね.