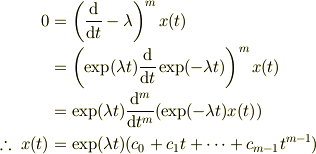単振動
単振動
石 さんの書込 (2009/07/08(Wed) 21:38)
はじめまして. 私は,資源系の大学の学生です. よろしくお願いします.
大学の物理学の授業で,以下のような問題を出されました.
単振動の周期Tの式を
ニュートンの運動方程式:F = m(d^2x/dt^2)
フックの法則:F = - kx
の式から導け.
※F:力m:質量x:x軸方向の変位k:バネ定数 t:時間T:周期
自分は,高校で物理を履修していませんでした. そこで,兄からもらった教科書を使って勉強してみましたが, 二階微分の形がどこにも載っておらず,またいきなり公式が出てきていて, どのようにして求めればいいのかがよく分かりません.
教科書は,『高等学校物理?』(数研出版,2003)を また大学では,『初等力学』(甲木伸一,2007,裳華房) を使用しています.
どうか宜しくお願い致します.
Re: 単振動
トビラ.. さんのレス (2009/07/08(Wed) 22:02)
多分ですが,周期運動を問題にしているので
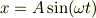
(  は角速度)
とおいて,これを代入してみてはいかがでしょうか?
三角関数の微分ができればできると思います.
後,角速度と周期の関係式は
は角速度)
とおいて,これを代入してみてはいかがでしょうか?
三角関数の微分ができればできると思います.
後,角速度と周期の関係式は  だったと思います.(速度×時間=距離なので・・・)
間違っていたらごめんなさい.
だったと思います.(速度×時間=距離なので・・・)
間違っていたらごめんなさい.
Re: 単振動
mNeji さんのレス (2009/07/08(Wed) 23:43)
石さん,初めまして.
解くべき微分方程式を書き出すとどうなりますか?出来れば,ω^2 = k/m で定義される定数を使ってください.
其れが出来たら,ややごり押し的な説明をしてみましょうか?
Re: 単振動
石 さんのレス (2009/07/09(Thu) 16:03)
トビラ..さん,mNejiさんはじめまして. そして,ご回答ありがとうございます.
解くべき微分方程式は,恐らく
F = m(d^2x/dt^2)…?
F = - kx…?
?,?から,Fは同じ力だと考えて,
- kx = m(d^2x/dt^2)
となります.
そうすると,トビラ..さんから教えて頂いた
x = A sin(ωt)より,
- k(A sin(ωt)) = m(d^2(A sin(ωt))/dt^2)
となり…,あれ?何だか返って複雑にしてしまったような….
単純に ω × T = 2πより
T = 2π/ω
では駄目なんでしょうかね? すみません,楽観視し過ぎました.
あと, >ω^2 = k/m で定義される定数
この定数ですが,授業では特に出てきませんでした.
Re: 単振動
mNeji さんのレス (2009/07/09(Thu) 16:19)
>?,?から,Fは同じ力だと考えて, >- kx = m(d^2x/dt^2) >となります.
この考え方でいいですが,習慣的に運動方程式の「左辺に質量X加速度」を,「右辺に掛かる力」を書きます.従って,
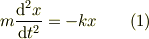
このように書くのは,左辺は単一項ですが,右辺はバネの力だけでなく,重力とか,摩擦力などと複数の項が出て来る事が多いからです.
実際に運動方程式(微分方程式)を解くときには,なるべく「m,k」などの定数部分を纏めます.今の場合,「ω^2 = k/m」と置くと,後の計算が楽になるからです.勿論,そのままでも構いません.ちなみに「ω」は角速度と言われます.
ちなみに,式(1)の左辺にだけ着目して,トビラ..さんの仰る 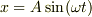 を入れて見るとどうなりますか?
を入れて見るとどうなりますか?
〜〜〜〜 私はこれから外出するので,夜に論議がなるとおもいます.
Re: 単振動
石 さんのレス (2009/07/09(Thu) 21:27)
お忙しいところ,ありがとうございます.
そうすると,(1)式より,
(d^2x/dt^2) = - (k/m) x
ω^2 = k/mより,
(d^2x/dt^2) = - ω^2 x
(1)式の左辺に,x = A sin(ωt)を代入すると
(d^2 A sin(ωt)/dt^2)
= (d/dt)(d A sin(ωt)/dt)
A sin(ωt)はx軸方向の変位ですから, (d A sin(ωt)/dt) = v※v:速さ よって,
= (d/dt)(v)
= (dv/dt)
となるのでしょうか? またどこか変ですかね?
Re: 単振動
mNeji さんのレス (2009/07/09(Thu) 23:14)
>A sin(ωt)はx軸方向の変位ですから, >(d A sin(ωt)/dt) = v※v:速さ
良い所まで来ていますね.x(t)はある時刻tの時のx軸方向の変位です.その速さv(t)は,色々な書き方があります; v(t) = dx(t)/dt = d/dt{x(t)}
同様に,その加速度α(t)も色々な表記法があります; α(t) = dv(t)/dt = d/dt{v(t)} = d/dt[d/dt{x(t)}] = (d/dt)^2{x(t)} = d^2/dt^2{x(t)}
で,いま x(t) = Asin(ωt)について考えるのですから,
v(t) = d/dt{x(t)} = d/dt{Asin(ωt)} = Aωcos(ωt) α(t) = d/dt{v(t)} = d/dt{Aωcos(ωt)} =-Aω^2sin(ωt) = -ω^2Asin(ωt) = -ω^2*x(t)
この結果を,運動方程式の左辺に適用すると, md^2/dt^2{x(t)} = mα(t) = -mω^2*x(t) = -m(k/m)*x(t) = -k*x(t)
無事に運動方程式の右辺に等しくなります.ですから,少なくとも「x(t) = Asin(ωt)」は与えられた微分方程式の解の一つである事が判ります.
ここまでで,判らない事がありますか?良かったら次に進みます.
Re: 単振動
mNeji さんのレス (2009/07/10(Fri) 00:54)
おそらく,本問に対する解法は少なくとも3つあると思います.
- 運動方程式にdxを掛けて積分し,運動エネルギーをxの関数として得た後,運動速度,v(t)をx(t)の関数と変形後に,xとtとに変数分離して求める.
- 正弦関数,余弦関数が,本問の運動方程式を満たす事を利用する.
- 本問の運動方程式を因数分解して,1階の微分方程式に分割して,直接に時間積分する.
〜〜〜〜 (1)は,きっと何処かの力学の教科書にでていると推測します. (2)は,トビラ..さんの方針で,すでに検討済み. (3)は,此れから....
Re: 単振動
トビラ.. さんのレス (2009/07/10(Fri) 01:14)
これを書いた後で気づいたのですが, mNejiさんと解法の仕方が違うので僕が今下に書いているやつ無視してくれて構いません.スミマセン,混乱させるようなことしてしまって ↓↓↓↓↓無視で!!でも,いつか余裕ができたら見てね(笑)
まず,三角関数の微分をおさらいしましょう.三角関数の微分は
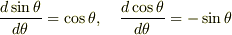 です.もしこの式がわからないなら言ってください.最初っから証明しますので.
です.もしこの式がわからないなら言ってください.最初っから証明しますので.
また,微分方程式は 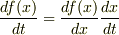 と変形できることはご存知ですか?なので,
と変形できることはご存知ですか?なので, 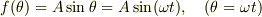 とおくと
とおくと 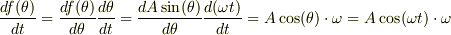 となります.
(
となります.
( 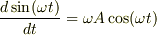 となる.)
これをもう一度,
となる.)
これをもう一度,  で微分するとつまり,
で微分するとつまり,

となります.これをよく覚えておいてください.
>T = 2π/ωでは駄目なんでしょうかね?
この 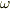 は問題文のどこにも存在しないので,この
は問題文のどこにも存在しないので,この 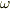 はまだ未知数ということになります.つまりは
はまだ未知数ということになります.つまりは 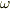 を求める必要があります.
我々は,この
を求める必要があります.
我々は,この 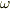 を
を 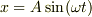 と定義しました.周期運動を考えているので,このように
と定義しました.周期運動を考えているので,このように  が三角関数になると思ったからです.こういった式を解くにはまず,「初めに大切な式をすべて書き出す」ことが重要ですから重要な式をまず,書き出します.
が三角関数になると思ったからです.こういった式を解くにはまず,「初めに大切な式をすべて書き出す」ことが重要ですから重要な式をまず,書き出します.
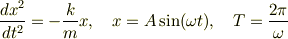
です.
ではここから解いていきます.と思ったけど,もうすべて教えたので後は自分で計算してみてください.ポイントなのは左の式と真ん中の式で, 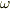 をもとめ,それを右の式の
をもとめ,それを右の式の 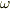 に代入すればそれが答えです.
に代入すればそれが答えです.
Re: 単振動
トビラ.. さんのレス (2009/07/10(Fri) 01:27)
ごめんなさい.僕の解答と,mNejiさんとの回答が違いますので,僕らの解答をごっちゃにするとややこしいですね.ほんとごめんなさい.
僕の解答無視でお願いします!!
多分mNejiさんの方が一般的なので.
Re: 単振動
mNeji さんのレス (2009/07/10(Fri) 09:32)
トビラ..さん,
>ごめんなさい.僕の解答と,mNejiさんとの回答が違いますので,僕らの解答をごっちゃにするとややこしいですね.ほんとごめんなさい. >僕の解答無視でお願いします!!
むしろ,トビラ..さんのやり方で,「三角関数が微分方程式とどのように関わるか」を知るのはとても重要だと思いました.
>多分mNejiさんの方が一般的なので.
その逆で,とても風変わりで厳密でもないので,手品みたいなものです.
Re: 単振動
石 さんのレス (2009/07/10(Fri) 15:29)
トビラ..さん,mNejiさん,どうもありがとうございます.
トビラ..さんの方法で行くとωは, ω^2 = k/mでしたから,
ω = +− √( k/m )と,なりますね.
T = 2π / ωより
T = 2π / ( +− √( k/m ) )
∴T = 2π * ( +− √( m/k ) )
これでよろしいでしょうか?
一方,mNejiさんの解き方では, >(3) 本問の運動方程式を因数分解して,1階の微分方程式に分割して, 直接に時間積分する.
とのことですが,自分はこの形の解き方を見るのは,多分初めてです. 一体,どのようにして解くのでしょうか? そもそも,運動方程式を因数分解できるのでしょうか? お願いします.
あと,質問ですが,sinθ のθは, sin(θ) のように,()でくくった方がいいですか?
Re: 単振動
mNeji さんのレス (2009/07/10(Fri) 16:04)
>あと,質問ですが,sinθ のθは, >sin(θ) のように,()でくくった方がいいですか?
これは好みの問題でもあります.「sinθ」のように単純な場合は表記が簡単ですのでどちらでも良いのかも知れませんが,「sin(θ-δ)」のような場合,「sinθ-δ」とすると; ・sin(θ-δ) ・sin(θ)-δ と間違い易いと思います.大昔,長い計算の一部で,この手のミスをして見つけるのに時間がかかった事があります.
其れ以来,その式をプログラムにする場合にそのまま打ち込める事を想定して常に括弧をつけて表記するようにしています.
#だから三角関数が嫌いで...,
ただし,上と矛盾しますが,exp(x)に対応する,e^(x)の場合,手書きやTeXでは間違え難い限り, 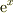 として括弧を省略します.ま,好みの問題ですからね.
として括弧を省略します.ま,好みの問題ですからね.
#だから指数関数が好きなのだろうと....
>そもそも,運動方程式を因数分解できるのでしょうか?
ごもっともなご指摘と思います.一般的に成り立つとは思えません.あくまでこの場かぎりだろうと思います.でも,私としては,エネルギー積分しかないのも寂しいと感じる訳です.続きは,また夜に書きます.
Re: 単振動
mNeji さんのレス (2009/07/11(Sat) 02:47)
>>そもそも,運動方程式を因数分解できるのでしょうか?
エアロバイクを漕ぎながら考えて居たのですが,私のやった事は,線形の微分方程式で,各階の微分の係数が定数であり,同次形の場合ならば成り立つもので,解をexp(λt)の形に仮定してn階微分方程式に代入し,λのn次多項式(特性方程式とも呼ぶ)を得て,そのn個の根,(λ1, λ2, ...,λn)を得て,その線形和で解を得るのと同じです.
#これらの事は,微分方程式を習う機会があれば,その時に思い出して下さい.
〜〜〜〜〜
ジムで運動のし過ぎで疲れ果てたので,続きは明日の夜になります.
Re: 単振動
石 さんのレス (2009/07/11(Sat) 15:20)
ありがとうございます.
>其れ以来,その式をプログラムにする場合に そのまま打ち込める事を想定して常に 括弧をつけて表記するようにしています.
そうだったんですか…. そうすると,mNejiさんは プログラミング関係のお仕事をなされているのですか?
(3)の解法はなかなか難しそうですね. どんな解き方なのか楽しみですが,余力があればお願いします.
Re: 単振動
mNeji さんのレス (2009/07/11(Sat) 20:14)
一般論を書こうかと思いましたが,今回の問題について説明します.恐らく間違いはないとは思いますが...,でも間違ったらご免なさいです.ま,軽い調子でみてください.
●解くべき問題
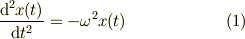
●準備 ・微分演算子について
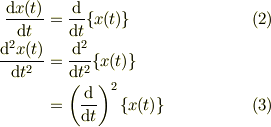
・因数分解について
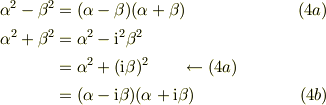
・1/xの不定積分
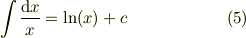
・対数関数の逆関数:指数関数
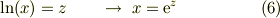
・指数関数←三角関数
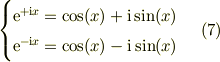
・指数関数→三角関数

●レッツ・ゴウ ・解くべき式を変形していく
![0 &= \frac{\mathrm{d}^2 x(t)}{\mathrm{d} t^2} +\omega^2 x(t) \qquad \leftarrow (1) \\&= \left( \frac{\mathrm{d} }{\mathrm{d} t} \right)^2 \{x(t)\}+\omega^2 x(t) \qquad \leftarrow (3)\\&=\left[ \left( \frac{\mathrm{d} }{\mathrm{d} t} \right) ^2+\omega^2 \right] x(t) \qquad \leftarrow (4b)\\&= \left[ \left( \frac{\mathrm{d} }{\mathrm{d} t} -\mathrm{i}\omega \right)\left( \frac{\mathrm{d} }{\mathrm{d} t} +\mathrm{i}\omega \right) \right] x(t) \qquad \leftarrow (9a)\\&= \left[ \left( \frac{\mathrm{d} }{\mathrm{d} t} +\mathrm{i}\omega \right)\left( \frac{\mathrm{d} }{\mathrm{d} t} -\mathrm{i}\omega \right) \right] x(t) \qquad \leftarrow (9b)](http://hooktail.maxwell.jp/bbslog/ea3937a8e6148f26ca38e84c34db4526.png)
・ここで視察により方程式(9a,b)の解は,下記二つの方程式の解の和であると<b>仮定</b>する.
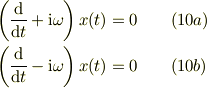
これらを,夫々,式(9)に代入すれば,遡って方程式(1)を満たすのは明らか.当然,その和も方程式の線形性から解である事は明白である...と思う(ここら辺は数学的に自信がないところ).
先ず,式(10a)を変形して見る;
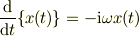
変数分離をする;
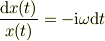
ちょっと 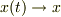 として見やすくする;
として見やすくする;

辺々を不定積分する(積分定数c');

よって,積分定数cとして

同様に式(10b)の解は,積分定数dとして

従って,微分方程式(1)の解は,一般的に

となる.
ここに式(7)を適用すると,積分定数a,b として;

となる.
〜〜〜〜 以上が大雑把な流れです.判らない所や可笑しい所があれば検討します.
なお,関連する論議が, 【微分方程式】数学迷い人 2009/07/01(Wed) 22:23 No.24431 にもあるので,ご覧になってください.
>>其れ以来,その式をプログラムにする場合に
学生のころのデータ解析で起こりました.当時は,簡単な計算でも,フォートランで(紙)カードにプログラムを打ち込んで,計算機センタにだして紙出力を眺めるという,面倒な作業でした.
>プログラミング関係のお仕事をなされているのですか?
そういう能力があったら良かったです.
Re: 単振動
トビラ.. さんのレス (2009/07/11(Sat) 22:36)
驚きです.そういう方法もあったんですね.読んでためになりました. (場合分けして求める同次2階微分方程式の解法だったら知ってましたが,)
Re: 単振動
mNeji さんのレス (2009/07/11(Sat) 23:44)
>(条件分けして求める同次2階微分方程式の解法だったら知ってましたが,)
そうですね,この場合も根を求めるのが面倒ですが因数分解出来れば同じ話になる訳ですね.勿論,重根だったら,乗数変化法を使うのが必要ですが....
恐らく,n次元同次定数係数微分方程式でも根 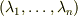 を求められれば,常に固有値方程式;
を求められれば,常に固有値方程式;
の解の線形和が一般解となる,と言い切れるのが嬉しい所かも知れません.
今更ながら,ディラックさんが相対論的な水素原子の波動関数を求めたときの話の凄さを思い浮かべます.
Re: 単振動
mNeji さんのレス (2009/07/12(Sun) 09:14)
石さん,
視点を変えて,ヤフー検索で「線形微分方程式特性方程式」を調べてみました.その先頭に,
「2階線形常微分方程式」 ・h ttp://www.sci.hokudai.ac.jp/~inaz/doc/B/math/node19.html
で,要領よく纏まった解説があるようなので,このサイトに従って理解された方が間違いない様に感じます.
その上,その最後には,別の解釈まで載っています(笑),ギャフンです.
また,その次の
「高階同次線形微分方程式の解」 ・ http://next1.cc.it-hiroshima.ac.jp/MULTIMEDIA/diffpub/node24.html
も解り易いと感じました.
現実の問題では,1階,2階の解法をしっかり理解していればいいので,あせる必要は無いと思いますが.
Re: 単振動
石 さんのレス (2009/07/12(Sun) 13:14)
mNejiさん,ありがとうございます.
本当に因数分解ができてしまうとは…. 何だか数学のマジックを見ているようです.
(3)の解き方は,習っていない内容も多いため, 今後勉強を重ねて理解できるように,努力したいと思います.
物理はわかるととても面白いものですね! 自分は,高校で物理を履修していないため,聴くこと見ること 全てが新鮮に感じます. mNejiさん,トビラ..さんには長きに渡り大変お世話になりました.
お二人のご好意を無駄にしないように, 確りと勉強に励みたいと思います.
それでは,どうもありがとうございました. 失礼致します.
Re: 単振動
toorisugari no Hiro さんのレス (2009/07/13(Mon) 10:29)
mNejiさん(9a)(9b)
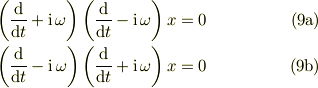
と
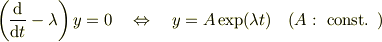
を使って,
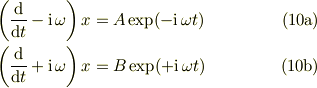
両式を引き算して
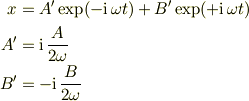
としてはどうでしょう.
# あるいは  が実関数であることを使って,(10b)の虚部のみを取り出して,
が実関数であることを使って,(10b)の虚部のみを取り出して,
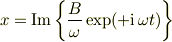
とした方がもっとスマートかな.
Re: 単振動
mNeji さんのレス (2009/07/13(Mon) 19:50)
toorisugari no Hiroさん,ご指導有り難うございます.
私は,微分方程式の因数分解が一般的に使えるかどうか良く判らなくて先週末は頭が混乱していました.漸く,自分でも少しは納得出来てきましたが,今ひとつ自分のやった事が判らないです.
自分としては,n次同次定数(実数)係数微分方程式が; (1) n個の1次同次定数(実数)係数微分方程式の積になり (2) それらを個々に積分して,加算すれば, n次同次定数(実数)係数微分方程式の一般解になる,と考えて良い様におもいました.
でも,例えば,速度の1次に比例する減速力を受ける運動の場合,
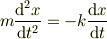
では, 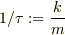 として,
として,

として,トリビアルな項がでてきてしまいます.でも,独立な解という意味では立派なような気もしますが....
#他方,特性方程式では単なる定数でしかありませんよね.
だから,因数分解できたとして,その解釈にまだ自信がありません.ここらで,数学力の無さを痛感します.
さて,ご説明戴いた; >mNejiさん(9a)(9b)
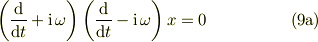
>と
 >を使って,
>を使って,
ですが,これは式(9a)を
![\left(\frac{\mathrm{d}}{\mathrm{d}t} + \mathrm{i\,}\omega\right) \left[ \left(\frac{\mathrm{d}}{\mathrm{d}t} - \mathrm{i\,}\omega\right)x \right] &= 0 \tag{9a}](http://hooktail.maxwell.jp/bbslog/408c92f963c4f5fdb3b64738b591680d.png)
と見て,y=[]の内部として積分を実行して式(10a)を得る.同様に式(10b)を得る.更にこの式(10a,b)より微分項を消去して一般解を得ると言う事でしょうかね.
確かに,二重積分から逃れると言う意味では興味深いですね.
また,
>(10a)の複素共役から,  が実関数であることを使って
が実関数であることを使って
も在りどうですが,頑固な私の脳ではまだ処理し切れていません.
自分としては,「運動方程式を初めて微分方程式で記述して,それを明快に積分して解を得る」という場面で,自信をもって説明する事ができると嬉しいと思います.
Re: 単振動
toorisugari no Hiro さんのレス (2009/07/14(Tue) 12:29)
> トリビアルな項がでてきてしまいます.でも,独立な解という意味では立派なような気もしますが....
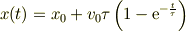
の定数項 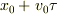 がそれに当たりますね.
がそれに当たりますね.
> と見て,y=[]の内部として積分を実行して式(10a)を得る.
はい,そうです.
Re: 単振動
mNeji さんのレス (2009/07/14(Tue) 14:21)
>の定数項 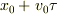 がそれに当たりますね.
がそれに当たりますね.
そうですよね.この場合,「定数項」というのも立派な一次独立な解の一つですね.
とすると,一般にn次の微分方程式を1次の微分方程式の積に因数分解すると考えて,その直接積分解の総和とするのは原理的にはokな気がしますが,何処かに落とし穴はありますか?勿論,重根の場合は別途としますが.
#非同次解についても,因数分解の方角から眺める事ができると面白そうですが...,まだ闇です.
Re: 単振動
toorisugari no Hiro さんのレス (2009/07/14(Tue) 14:50)
> 何処かに落とし穴はありますか?勿論,重根の場合は別途としますが.
重根の問題以外に落とし穴はありません.でも,重ね合わせの原理をつかうなら,  を代入して代数方程式を解くという,標準的な方法がわかりやすいでのは?
を代入して代数方程式を解くという,標準的な方法がわかりやすいでのは?
Re: 単振動
mNeji さんのレス (2009/07/14(Tue) 15:23)
toorisugari no Hiroさん,
>重ね合わせの原理をつかうなら,素直に  を代入して代数方程式をとく,標準的な方法がわかりやすいでのは?
を代入して代数方程式をとく,標準的な方法がわかりやすいでのは?
そうですね.自分の場合,初めて微分方程式を知ったころ,この振動にぶつかり,直接積分で解を得ようとして頑張ったものの,仕事の積分を噛まさなければならないので,不満でした.
それいらい,「素直に  を代入」を見ると,そのときの「イライラ」を思い出して,情けない感じを受けていました.で,今回のご質問を拝見していて,再挑戦になった訳です.
を代入」を見ると,そのときの「イライラ」を思い出して,情けない感じを受けていました.で,今回のご質問を拝見していて,再挑戦になった訳です.
細かな話題にご教示を戴き,有り難うございました.
石さん,
若い頃に感じていた疑問が,漸く解けた気がします.お蔭で,実数関数の微分方程式と複素数の関係や固有値・固有関数の関係を実体験できるようになりました.
実際には,「素直に  を代入」をお勧めしますが,その背景はこうだろうと思います(笑).
を代入」をお勧めしますが,その背景はこうだろうと思います(笑).
素敵な「資源」を探索されます様に.
Re: 単振動
toorisugari no Hiro さんのレス (2009/07/14(Tue) 20:50)
> 「素直に  を代入」を見ると,そのときの「イライラ」を思い出して,情けない感じを受けていました.
を代入」を見ると,そのときの「イライラ」を思い出して,情けない感じを受けていました.
こういう方法はどうでしょう.本質的には前に出した方法と同じですが.
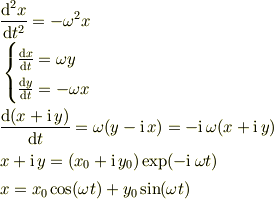
Re: 単振動
mNeji さんのレス (2009/07/14(Tue) 22:03)
>こういう方法はどうでしょう.本質的には前に出した方法と同じですが.
確かに,他の方の説明を拝見していると,初心者に直感的に,かつ解り易い式の流れの元に説明するというのは,とても難しいものですね.
Re: 単振動
mNeji さんのレス (2009/07/15(Wed) 13:42)
■重根のある場合について
本来のご質問とはかけ離れますが,一寸コメントさせて戴きます.
今,ある固有値 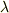 が「m重に縮退」しているとします.この場合,因数分解の結果,方程式は;
が「m重に縮退」しているとします.この場合,因数分解の結果,方程式は;
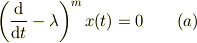
となりますます.
●「m=1」の場合
直接積分により,解は;
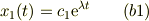
となります.
●「m=2」の場合
この解を定数変化法で
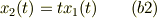
と仮定すると;
![\left( \frac{\mathrm{d} }{\mathrm{d} t} -\lambda \right)^2 x_2(t)&= \left( \frac{\mathrm{d} }{\mathrm{d} t} -\lambda \right)\left[ \left( \frac{\mathrm{d} }{\mathrm{d} t} -\lambda \right) tx_1(t) \right]\\&= \left( \frac{\mathrm{d} }{\mathrm{d} t} -\lambda \right)\left[ x_1(t) +t\frac{\mathrm{d} }{\mathrm{d} t}x_1(t)-\lambda x_1(t)\right]\\&= \left( \frac{\mathrm{d} }{\mathrm{d} t} -\lambda \right)\left[ x_1(t) +t \left( \frac{\mathrm{d} }{\mathrm{d} t} -\lambda \right)x_1(t)\right] \quad \leftarrow (b1)\\&= \left( \frac{\mathrm{d} }{\mathrm{d} t} -\lambda \right)\left[ x_1(t)\right] \quad \leftarrow (b1)\\&= 0 \qquad (a2)](http://hooktail.maxwell.jp/bbslog/a8a8fe424895c8e0f65dccfde02053d5.png)
●「m重に縮退」の場合
従って,「m重に縮退」縮退している場合,m個の関数が固有関数となる;
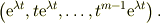
以上.
Re: 単振動
mNeji さんのレス (2009/07/15(Wed) 17:42)
まだ理解し切っていないのですが,雰囲気は判ります,漸く考えさせて頂きます.取り急ぎ,お礼まで.
#元々,古典力学の振動を考えていた訳ですが,微分方程式や量子力学の問題を見ている様な錯覚を覚えてしまいます.
Re: 単振動
mNeji さんのレス (2009/07/16(Thu) 12:38)
宿題の
>関係式
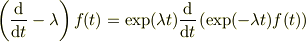
>を使うと
を少し考えて見ましたが,やはり右辺の演算子の関数への掛かり方が,難しいですね.この気持ちとしては,

という感じでいいのでしょうか.「割って・掛けて,チャラ」という連鎖になるのかな.そうすると
![\left( \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t)\right\} \right)^2 f(t) &= \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t)\right\}\left[ \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t)\right\}f(t)\right]\\&= \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t)\right\}\left[ \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t)f(t)\right\}\right]\\&= \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t) \left[ \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t)f(t)\right\}\right]\right\}\\&= \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t) \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t)f(t)\right\}\right\}\\&= \exp(\lambda t) \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \frac{\mathrm{d}}{\mathrm{d}t}\left\{ \exp(-\lambda t)f(t)\right\}\right\}\\&= \exp(\lambda t) \left( \frac{\mathrm{d}}{\mathrm{d}t}\right)^2 \left\{ \exp(-\lambda t)f(t)\right\}](http://hooktail.maxwell.jp/bbslog/acb8770603d59e596b52e6711a611ade.png)
なんとなく....
Re: 単振動
toorisugari no Hiro さんのレス (2009/07/16(Thu) 15:20)
そもそも微分演算子と括弧の関係は微妙ですよね.
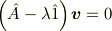
はOKだけど,
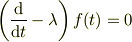
は「微分は括弧の外に影響与えない」
 という約束を破るわけですから.
という約束を破るわけですから.
演算子としての関係式

のときは 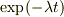 を関数と考えず,演算子と考えるべきです.また,演算子を囲む括弧があってもそれは代数演算の結合を表しているだけで,微分演算子が作用する範囲を表しているのではないと考えるべきです.
を関数と考えず,演算子と考えるべきです.また,演算子を囲む括弧があってもそれは代数演算の結合を表しているだけで,微分演算子が作用する範囲を表しているのではないと考えるべきです.

この段階で微分が指数関数に作用することは考えません.ただ, 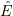 と
と 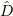 が非可換であることが要求されているだけです.
が非可換であることが要求されているだけです.
演算子 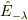 は関数に作用して初めて,
は関数に作用して初めて,
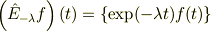
関数の積を値に持つ新しい関数になり,その後に微分演算子を 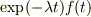 という関数に作用させると考えます.
という関数に作用させると考えます.
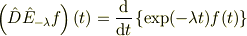
# ここでの{}は微分の対象となる範囲を表します. つまり
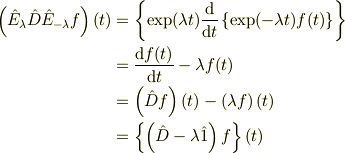
となり,これは任意の関数 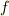 ,任意の実数
,任意の実数  に関して成り立つので,
に関して成り立つので,
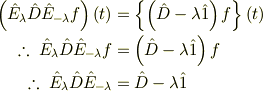
となり最初に示した,演算子としての等式が得られます.
Re: 単振動
mNeji さんのレス (2009/07/16(Thu) 18:45)
>演算子としての関係式
 >のときは
>のときは  を関数と考えず,演算子と考えるべきです.また,演算子を囲む括弧があってもそれは代数演算の結合則を表しているだけで,微分演算子がかかる範囲を表しているのではないと考えるべきです.
を関数と考えず,演算子と考えるべきです.また,演算子を囲む括弧があってもそれは代数演算の結合則を表しているだけで,微分演算子がかかる範囲を表しているのではないと考えるべきです.
な〜〜〜るほど,ですね.実際に(m=1,2)とやって見て実感しました.
>関数の積を値に持つ新しい関数になり,その後に微分演算子を  という関数に作用させると考えます.
という関数に作用させると考えます.
などに付いても,線形代数系統の本を覗いて感触をつけて見たいです.
で,本題に戻って,「m重に縮退の場合」の方程式の解が,「m-1次の多項式の解」となることの (演算子法もどき)の考え方を理解出来ました.この目で見れば,演算子法を素直に理解出来るだろうと思います.恐らく,その後に非同次解の解を形式的に求める事が理解出来る様になると期待しています.
かなり話が逸れてしまいましたが,ご説明有り難うございました.
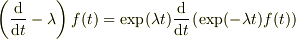 を使うと
を使うと