行列の乗算
行列の乗算
トビラ.. さんの書込 (2009/07/07(Tue) 21:43)
こんばんは
行列の乗算について今日一日中考えていたのですが,どうしても納得できなかったんですけど,どなたか僕に説明お願いします.
行列 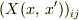 と行列
と行列 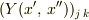 の乗算は
の乗算は
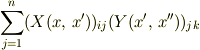
ではなく,
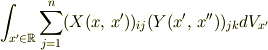
となるのですが,どうしてそれぞれの行列の成分が変数 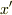 の関数となっていたとき,このように積分することになるのでしょうか?
離散近似などを用いいろんな方法で理解しようとしたのですが無理でした.(たとえば
の関数となっていたとき,このように積分することになるのでしょうか?
離散近似などを用いいろんな方法で理解しようとしたのですが無理でした.(たとえば 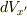 が現れる理由がわからない.)
今日一日中考えていて理解できなかったのでどうか,どうかわかる方無知な僕に教えてくださると助かります.
が現れる理由がわからない.)
今日一日中考えていて理解できなかったのでどうか,どうかわかる方無知な僕に教えてくださると助かります.
Re: 行列の乗算
トビラ.. さんのレス (2009/07/07(Tue) 22:11)
簡単のため 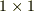 次元の2つの行列,
次元の2つの行列,  を考え,
を考え, 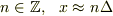 として,この離散近似を用いると,この2つの行列は
として,この離散近似を用いると,この2つの行列は
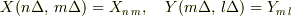 となり,これは行列(2階のテンソル?)そのものであるからこの行列の乗算は
となり,これは行列(2階のテンソル?)そのものであるからこの行列の乗算は
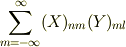
で,・・・・このままだとただの行列なので,両辺に 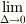 をかけてこの極限でもとの連続変数にもどすと・・・
と思ったんですが,やっぱり,このままだと,
をかけてこの極限でもとの連続変数にもどすと・・・
と思ったんですが,やっぱり,このままだと, 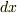 が生まれないので,積分の形にならないです・・・なぜなんでしょう?
が生まれないので,積分の形にならないです・・・なぜなんでしょう?
Re: 行列の乗算
トビラ.. さんのレス (2009/07/07(Tue) 23:00)
上述の式を変形すると
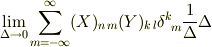
ここで,離散近似を用いたデルタ関数は 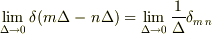 とかけるので,
とかけるので,
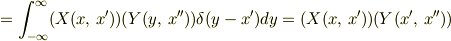
となって,定数型(?)の行列の乗算を,そのまま極限で,変数型の行列にかえると,この式を見ればわかるようにここには積分は含まれていません.つまり,積分の形にするのは不自然ではないでしょうか?
たしかに,変数  を消したいというのはわかりますが,どうして積分なのでしょか?
を消したいというのはわかりますが,どうして積分なのでしょか?
Re: 行列の乗算
トビラ.. さんのレス (2009/07/07(Tue) 23:26)
ん?
・・・もしかして,ただたんに変数 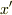 を消したかったから,合計を取っただけなのでしょうか?
???
を消したかったから,合計を取っただけなのでしょうか?
???
Re: 行列の乗算
トビラ.. さんのレス (2009/07/08(Wed) 00:11)
あ,わかったかも,
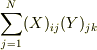 において,
において, 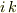 を固定し
を固定し 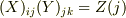 と定義し,横軸を
と定義し,横軸を 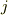 軸,とし,縦軸を
軸,とし,縦軸を 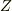 とすると,
とすると, 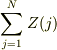 は,
は, 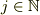 なので,一本一本の太さが1のリーマン和とも考えられる.つまり,
なので,一本一本の太さが1のリーマン和とも考えられる.つまり, 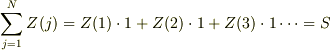 (面積).よってこのことから行列成分が定数の行列の乗算はこの意味で「面積を求めることである」ともいえる.(と思う.)したがって,行列の成分が変数
(面積).よってこのことから行列成分が定数の行列の乗算はこの意味で「面積を求めることである」ともいえる.(と思う.)したがって,行列の成分が変数 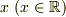 の関数の行列の乗算も面積を求めるべきである.したがって,「積分するべき」である.(ただし,ここでは,乗算のもととなった2つの行列に同じ変数がそれぞれ現れた場合だけその変数に対してだけ変数扱いした)
ということなのかな?もしかして,
の関数の行列の乗算も面積を求めるべきである.したがって,「積分するべき」である.(ただし,ここでは,乗算のもととなった2つの行列に同じ変数がそれぞれ現れた場合だけその変数に対してだけ変数扱いした)
ということなのかな?もしかして,
ってか,思いっきり独り言じゃん!!!!!
Re: 行列の乗算
mNeji さんのレス (2009/07/08(Wed) 01:33)
トビラ..さん,こういった数学が前面に出て来た問題はアンタチャブルと思っているのですが....
最近,量子力学を少し思い出し気味です.例えば,ある固有値問題;
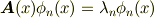
が在った場合,固有値に縮退がなければ;
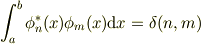
と直交規格条件がでますね.
これを,状態nの連続ヴェクタ 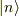 の共役転置と状態mの連続ヴェクタ
の共役転置と状態mの連続ヴェクタ 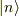 との内積とも見なせると考えるような感じ.そこで,強引に;
との内積とも見なせると考えるような感じ.そこで,強引に;
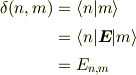
のように解釈できませんでしょうか?
似た様に,2変数の関数の変数を如何にも添字についての和みたいに考えてしまたらどうでしょうか.やはり支離滅裂かな.変数 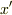 についての共役転置行ヴェクタ,
についての共役転置行ヴェクタ, 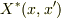 と,やはり変数
と,やはり変数 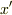 についての内積で構成される2変数のマトリクス関数,Z(x,x'')
についての内積で構成される2変数のマトリクス関数,Z(x,x'')
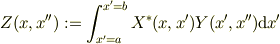
見たいな?
Re: 行列の乗算
トビラ.. さんのレス (2009/07/08(Wed) 03:51)
こんばんは,mNejiさん,,眠い,.
>トビラ..さん,こういった数学が前面に出て来た問題はアンタチャブルと思っているのですが....
芸人の?・・・ん〜・・・・
数学にとってのアンタッチャブルは,避けるものではなく触れるのもです!!!!
って詭弁を言ってみる..・・・眠い.,
>が在った場合,固有値に縮退がなければ;
すみません,なんかこのあたりの計算,数学的についていけないようです.僕・・・
うーん.1つの行列としてみたときの成分としては,積分をとっていないのに乗算をしたらたちまち積分がつくっていうのが納得できなかったんです(各成分で積分をとっていてもそうはならないけどね).例え,そのように首尾一貫して行列の乗算を定義したからといっても納得できなかったんです.例えばいま,ディラック括弧という公式を学んでいるんですけど,その公式には行列の乗算の項がります.例えばその任意の 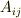 に定数の行列
に定数の行列 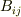 を代入しても積分は現れません.ただし,
を代入しても積分は現れません.ただし, 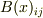 と
と  の関数なら積分が当然のように現れるんです.ということは,この乗算の時に現れる積分はまったく独立して任意に定義したわけではなく,必然的にそうしなくてはならないものと思ったんです.そう思った以上数学的にきちんと証明できなくてはなりません.
確かに
の関数なら積分が当然のように現れるんです.ということは,この乗算の時に現れる積分はまったく独立して任意に定義したわけではなく,必然的にそうしなくてはならないものと思ったんです.そう思った以上数学的にきちんと証明できなくてはなりません.
確かに
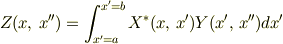
とすれば,左辺の変数は 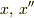 になりますが,
になりますが,
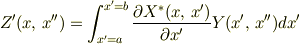
と定義しても左辺の変数は 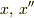 となるんじゃないでしょうか?このように乗算を定義することもできたはずです.
しかし,独り言を言っていたら理解できたようです.つまりは,定数行列の乗算はリーマン和と解釈できるため,離散近似で考えると,離散変数を連続変数に変える極限で積分になると理解できました.
独り言に終わらなくてよかったです..
僕ももうおねむの時間なので,お先に寝ます.おやすみなさい.(もう4時か…)
となるんじゃないでしょうか?このように乗算を定義することもできたはずです.
しかし,独り言を言っていたら理解できたようです.つまりは,定数行列の乗算はリーマン和と解釈できるため,離散近似で考えると,離散変数を連続変数に変える極限で積分になると理解できました.
独り言に終わらなくてよかったです..
僕ももうおねむの時間なので,お先に寝ます.おやすみなさい.(もう4時か…)
Re: 行列の乗算
mNeji さんのレス (2009/07/08(Wed) 09:24)
トビラ..さん,あんまり早朝まで頑張っていると体に毒ですよ.せいぜい週に1回とか制限を向けた方が良いかも知れません.(体験モード)
>例えばいま,ディラック括弧という公式を学んでいるんですけど,その公式には行列の乗算の項がります.
そうか,今頃気が付きました.トビラ..さんは量子重力のような分野に進もうとされているのでしょうか.だとすると,ディラックの量子力学をさらっと読むのが吉かも知れません.そのあと,近代的な量子力学の本,以前,toorisugari no Hiroさんから教えて戴いた「J.J.サクライの量子力学 上下」の系統を見られたらと思います.
#自分は,「J.J.サクライの量子力学」を神田の古本屋さんで拝見しましたが,今更量子力学の本を購入するのが恥ずかしくて,流体力学の本に化けてしまいました. #その後,膝をケガしてしまったので,お茶の水の界隈に行く事ができなくなってしまいました.あのとき買っていたら,ケガからのがれられたか? #流石に区の図書館には,この本は置いてありません(泣).
Re: 行列の乗算
toorisugari no Hiro さんのレス (2009/07/08(Wed) 10:14)
離散ベクトル(有限次元)から連続ベクトル(無限次元)への展開で悩まれているようですね.やはり,量子力学や場の理論を学ばれるのが一番早道かもしれません.
量子力学では位置演算子 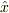 の固有ベクトル
の固有ベクトル 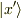
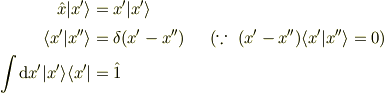
は連続ベクトルであり,演算子 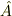 は
は
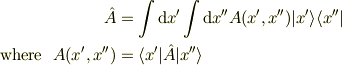
と行列成分 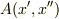 を使って表されるというように,連続ベクトルの取り扱いが多くみられます.
を使って表されるというように,連続ベクトルの取り扱いが多くみられます.
これらを学んで感覚を掴まれることを勧めます.
# JJ.Sakurai -> Dirac -> Landau(Classical field) -> Quantum field というpath ですかね.
Re: 行列の乗算
トビラ.. さんのレス (2009/07/08(Wed) 21:50)
>トビラ..さんは量子重力のような分野に進もうとされているのでしょうか
物理学者だったら誰もが一度はあこがれる,場の統一の分野に進みたいと思ってます.
># JJ.Sakurai -> Dirac -> Landau(Classical field) -> Quantum field というpath ですかね.
toorisugari no Hiroさんの助言とあらばメッチャ読んだ方がいいですね.(笑) ただ,僕も心にこれはだけは読みたいと思っている本があるので,いろいろ試行錯誤しながら,どの本を読むか決めていこうと思います. お勧めの本を紹介していただいてどうもありがとうございます.
Re: 行列の乗算
mNeji さんのレス (2009/07/19(Sun) 20:48)
最近,量子力学の教科書をすこしく齧り直しています.その為に,市営図書館の新刊書をウオッチしています.そこで,
書名 量子力学 著者名 倉本義夫著江澤潤一著 出版社 東京朝倉書店 出版年月 2008.4 価格 3400円 ページ数 9,216p 大きさ 21cm シリーズ名 現代物理学〈基礎シリーズ〉1倉本義夫編集江澤潤一編集 ISBN 9784254137712
という図書を拝見しました.
この本は,東北大学の物理学科の量子力学の中級から上級の題材についての教材資料を目指しているようです.
自分は電磁気から量子力学を眺めるという変な勉強をして来たので,手短に量子力学を復習するという意味では面白そうです.
さらにp178から「ハミルトニアンの因子化と超対称性」という論議があり,線形微分方程式の因数分解に凝り出した自分としては,とても参考になりそうです.
Re: 行列の乗算
トビラ.. さんのレス (2009/07/24(Fri) 23:32)
今晩ワン 超対称性ってなんかひかれる言葉ですね. 今度目をとおしてみます.理解できないだろうけども・・・(笑)