量子力学の基礎

home > 掲示板 >

このページのPDF版

サイトマップ

量子力学の基礎

huma さんの書込 (2009/07/06(Mon) 15:30)

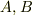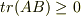正値な演算子 A,B に対して $tr(AB)\geq0$ となることを証明するにはどうしたらいいですか？？Bの固有ベクトルから正規直交基底を作って解けばいいのですか？？分かるかたいたらお願いします．

Re: 量子力学の基礎（追加）

huma さんのレス (2009/07/06(Mon) 15:36)

正値の演算子って言うのは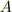が正値の演算子だったら，任意のuに対して 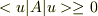$<u|A|u>\geq0$ ということです．

Re: 量子力学の基礎（追加）

mNeji さんのレス (2009/07/07(Tue) 00:52)

humaさん，数学的な詳しい事は判りませんが，ブラケット形式で考えてみます．

＞Bの固有ベクトルから正規直交基底を作って解けばいいのですか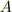？？＞が正値の演算子だったら，任意のuに対して 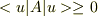$<u|A|u>\ge 0$ ということです．

これをそのまま，式にしただけみたいですが．

ABのトレース

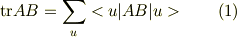
$\mathrm{tr}AB = \sum_u <u|AB|u> \qquad (1)$

|u>はBの固有関数で直交関数系を成し，完全性を満たす；

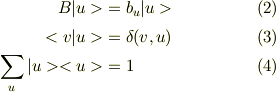
$B|u> &= b_u |u> &\ (2)\\<v|u> &= \delta(v,u) &\ (3)\\\sum_u |u><u> &=1 &\ (4)$

A,Bは正値の演算子

$<u|A|u>\quad \ge \ 0 \qquad (5)\\<u|B|u>\quad \ge \ 0 \qquad (6)$

以上の材料から，何か言えませんか？

Re: 量子力学の基礎（追加）

toorisugari no Hiro さんのレス (2009/07/07(Tue) 11:31)

残念ながら

$\mathrm{tr}(AB) &= \sum_u \langle u|AB|u \rangle\\&= \sum_u \langle u|A \left(\sum_{v}|v\rangle\langle v|\right) B|u \rangle\\&= \sum_{u,v} \langle u|A|v\rangle ~\langle v|B|u \rangle$

であり，簡単にはいきません．難しい問題ですね．

Re: 量子力学の基礎（追加）

mNeji さんのレス (2009/07/07(Tue) 12:05)

どこが落とし穴なのか判りませんが，敢えて無謀を続けると，

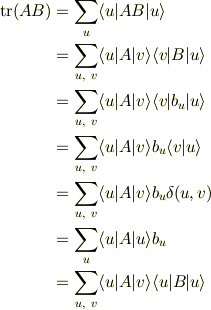
$\mathrm{tr}(AB) &= \sum_{u} \langle u|AB|u \rangle\\&= \sum_{u,\ v} \langle u|A|v\rangle\langle v|B|u \rangle\\&= \sum_{u,\ v} \langle u|A|v\rangle\langle v|b_u|u \rangle\\&= \sum_{u,\ v} \langle u|A|v\rangle b_u\langle v|u \rangle\\&= \sum_{u,\ v} \langle u|A|v\rangle b_u\delta(u,v)\\&= \sum_{u} \langle u|A|u\rangle b_u\\&= \sum_{u,\ v} \langle u|A|v\rangle\langle u|B|u \rangle$

＃「langle，rangle， ~」の存在に初めて気が付きました．有り難うございます．

Re: 量子力学の基礎（追加）

yutaka さんのレス (2009/07/07(Tue) 12:11)

はじめまして，1次元調和振動子の固有関数を用いて，ABの行列要素を計算するのはどうでしょう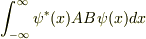． $\int_{-\infty}^{\infty}\psi^*(x)AB\psi(x)dx$

Re: 量子力学の基礎（追加）

toorisugari no Hiro さんのレス (2009/07/07(Tue) 12:16)

yutakaさん >> 別の問題なら，記事を消して別スレッドを立ててください． >> あと，問題が完全でありません．完全な問題を書いてください．

すいません．followだったんですね．上の文は取り消します．

Re: 量子力学の基礎（追加）

toorisugari no Hiro さんのレス (2009/07/07(Tue) 12:22)

mNejiさん

$\mathrm{tr}(AB) &= \sum_{u}\langle u|AB|u\rangle &(\langle u|u'\rangle=\delta_{u,u'},\sum_{u}|u\rangle\langle u| = 1)\\\text{where~}\\B|u\rangle &= b_u |u\rangle ~\left(b_u \geq 0\right)$