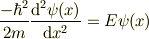球対称の状態のエネルギー固有値

球対称の状態のエネルギー固有値

えり さんの書込 (2009/07/06(Mon) 00:45)

すみません．以前立てたスレに顔を出せずにいるまま別の質問をさせていただいています…

「半径aの内部に閉じ込められている粒子を考えよう．これは無限に深い三次元の井戸型ポテンシャルで表される．(V(r)=0(r<a),V(r)=∞(r>a)) 球対称の状態の固有関数は 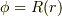\phi=R(r) と表される．球対称の状態に対してシュレーディンガー方程式を求めなさい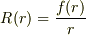．( R(r)=\frac{f(r)}{r} と書き直す)」

という問題で，問題文どおりに解いていったら，うまく解けなそうで投稿しました．下のように正攻法で解いていったのですが，どうでしょうか．

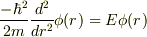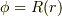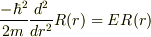
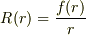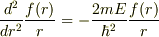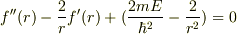
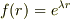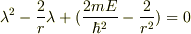r<aでのシュレーディンガー方程式は \frac{-\hbar^{2}}{2m}\frac{d^{2}}{dr^{2}}\phi(r)=E\phi(r) であるから， \phi=R(r) とおくと， \frac{-\hbar^{2}}{2m}\frac{d^{2}}{dr^{2}}R(r)=ER(r) R(r)=\frac{f(r)}{r} と書くと， \frac{d^{2}}{dr^{2}}\frac{f(r)}{r}=-\frac{2mE}{\hbar^{2}}\frac{f(r)}{r} 整理すると f''(r)-\frac{2}{r}f'(r)+(\frac{2mE}{\hbar^{2}}-\frac{2}{r^{2}})=0 f(r)=e^{\lambda r} とおくと \lambda^{2}-\frac{2}{r}\lambda+(\frac{2mE}{\hbar^{2}}-\frac{2}{r^{2}})=0 …

と解こうと思ったのですが，これで上手くいくでしょうか… どなたかアドバイスをいただけたら幸いです．よろしくお願いします．

Re: 球対称の状態のエネルギー固有値

mNeji さんのレス (2009/07/06(Mon) 15:06)

「球対称の状態」というのが良く判らないのですが，中心力(central force)のポテンシャルのもとに運動する粒子の角運動量がゼロの場合のエネルギ固有状態を考えろ，と解釈できると思います．

ついては，三次元のラプラシアンの極座標表示と，動径変数と角度変数の変数分離のプロセスについて教科書を見直すことをお勧めします．恐らく，f(r)の微分方程式は一次元の運動方程式と同一形式になるのだと思います．

Re: 球対称の状態のエネルギー固有値

えり さんのレス (2009/07/06(Mon) 23:56)

ご回答ありがとうございます．この問題もR(r),Θ(θ),Φ(φ)の変数分離を行うのですか…？ 先生がR(r)=f(r)/rとおくようにとおっしゃっていたので，てっきりrだけの関数になると思っていました．．

では，私の解き方は間違っていそうですね(汗

Re: 球対称の状態のエネルギー固有値

mNeji さんのレス (2009/07/07(Tue) 00:15)

＞この問題もR(r),Θ(θ),Φ(φ)の変数分離を行うのですか…？

原則論としてそう考えて，だけど「角運動量＝０」の固有状態だから，R(r)だけを考えるので良いですね．

＞先生がR(r)=f(r)/rとおくようにとおっしゃっていたので，てっきりrだけの関数になると思っていました．．

そして，このような「R(r)=f(r)/r」を導入すると，「f(r)」は一次元の場合の波動関数が従うシュレディンガー方程式にしたがうのではありませんか？，といいたかったのですが．

＞では，私の解き方は間違っていそうですね(汗

う〜ん，この場合の動径方向のシュレディンガー方程式は，

\frac{1}{r^2}\frac{\mathrm{d}}{\mathrm{d} r}\left( r^2\frac{\mathrm{d} R(r)}{\mathrm{d} r}\right) +\frac{2m}{\hbar^2}[E-V(r)]R(r) = 0

ですよね．これに「R(r)=f(r)/r」を代入すると？

Re: 球対称の状態のエネルギー固有値

えり さんのレス (2009/07/13(Mon) 19:03)

返信遅れて申し訳ありません．動径方向のシュレーディンガー方程式はわかりました．この場合はV(r)はないので無視してしまっていいのですよね？

あれから先生とも相談しながら，かぎしっぽを参考にしながら，やってみました． 無事

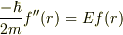\frac{-\hbar}{2m}f''(r)=Ef(r) という形になりました．これで大丈夫そうです． ありがとうございました．

Re: 球対称の状態のエネルギー固有値

mNeji さんのレス (2009/07/13(Mon) 20:10)

そうですね， ＞V(r)はないので無視

できれば，領域に限定があるものの，一次元の運動方程式；

\frac{-\hbar^2}{2m}\frac{\mathrm{d}^2 \psi(x)}{\mathrm{d} x^2} = E\psi(x)

と同じ形式に従うと思います．

Re: 球対称の状態のエネルギー固有値

えり さんのレス (2009/07/13(Mon) 22:02)

なるほど． だからこの問題の最後には一次元の井戸型ポテンシャルと比較する問いがあるんですね．(ここには書き込んでいませんが，そのような問題があったのです．)

ありがとうございました．

Re: 球対称の状態のエネルギー固有値

mNeji さんのレス (2009/07/13(Mon) 22:36)

＞だからこの問題の最後には一次元の井戸型ポテンシャルと比較する問いがあるんですね．(ここには書き込んでいませんが，そのような問題があったのです．)

こうして拝見していると，とても良心的な出題をして戴いていると思います．私にもそんな教官がいたら，量子力学がもう少し好きになっていたかと感じます．

今回の問題も，「量子力学；QM」での動径方向の処理が，「古典力学；CM」とひと味違う事を見せつけてくれたのでしょう．ですから，角度依存性を入れると，遠心力の処理(角運動量の処理)について，QMとCMとでどう違うかを味わえるのでしょうね．