演算子

rarara さんの書込 (2009/07/03(Fri) 11:56)

質問です．変な質問かもしれませんが 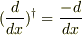$(\frac{d}{dx})^\dagger =\frac{-d}{dx}$ となるのはなんでですか？？？

「

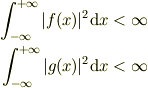
$\int_{-\infty}^{+\infty}|f(x)|^2\mathrm{d}x &< \infty\\\int_{-\infty}^{+\infty}|g(x)|^2\mathrm{d}x &< \infty$

となる実数値関数 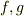f,g に対して，「内積」が

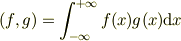
$(f,g)&=\int_{-\infty}^{+\infty}f(x)g(x)\mathrm{d}x$

で定義されるとする．

ある演算子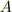の「転置」演算子 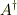$A^\dagger$ は，上の条件を満たす任意の 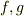f,g に対して

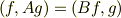
となる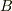のことである．」 # 実際は複素数値関数で定義するべきなんだけど，簡単のため実数値関数で定義しました．

これより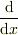， $\frac{\mathrm{d}}{\mathrm{d}x}$ の「転置」演算子は 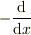$-\frac{\mathrm{d}}{\mathrm{d}x}$ であることが，部分積分法により導かれます．