数学迷い人 さんの書込 (2009/07/01(Wed) 22:23)

お久しぶりです↓

今回は，微分方程式に関して，ヒントを頂ければと思い投稿いたしました．

? y'=(x+y+2)/(x+1) ?y'-y=sinx ?y''+4y=x^2

?は，y'=1+ (y+1/x+1) ?は，まず右辺を0として計算して，基本解，e^(2i),e^(-2i)を求め，ロンスキャンを使って計算してみました．また複素数iは定数と同じ扱いで計算して良いのでしょうか？ 一通り，微分方程式を学んだつもりですが，どこでどのパターンを使えば良いかがわかりません．多くの演習が必要ですね・・・．

transfer さんのレス (2009/07/01(Wed) 23:09)

(1)は，y + 1 = η, x + 1 = ξ とでも置けば，もっと簡単な式になります．

(2)と(3)は共通に扱えて，x による微分を D と表すと， (2) (D - 1) y = sin x (3) (D^2 + 4) y = x^2 となるので，まずは右辺がゼロの解を求めて，それに右辺がゼロでない場合の特解を付け加えればいいです． つまり， (2) (D - 1) y = 0 (3) (D^2 + 4) y = 0 を最初に解きます．

ところで(3)の基本解は指数関数でも三角関数でもどちらでもいいですよね． e^{i 2 x}とe^{- i 2 x}は，sin 2x とcos 2x にできますから． （指数関数の場合は複素数の定数係数となり，三角関数の場合は実数の定数係数になります）

数学迷い人 さんのレス (2009/07/02(Thu) 00:01)

ご回答ありがとうございます．

しかし，，，，

?をそのように変形すると，関係ない変数が2つあり，ますます手がつきません． ??で，Dとおくとありますが，その手法は一般的ですか？ Dの扱いがいまいち理解できません． せっかくお答えいただいたのに，わからずやで申し訳ございません．

もし，よろしければ，もう少し詳細をいただきたいです．

transfer さんのレス (2009/07/02(Thu) 00:32)

同次型の微分方程式になるはずですが， dη/dξ = (ξ + η)/ξ となりますよね． それで，さらに，η = u ξ とするとどうでしょう？ ここで，u は ξ の関数と考えます．

(2)と(3)のやり方は一般的です．演算子法といいます． 要は，微分方程式を D の代数方程式に置き換える手法ですから， (2)は，D - 1 = 0 (3)は，D^2 + 4 = 0 を解いて，その求まった D を指数関数で e^{D x} とすれば解になります． 逆に，y = e^{D x} と解を仮定して，D を求めると考えても同じです．

mNeji さんのレス (2009/07/02(Thu) 04:07)

(3)の強制解(特解)について考えます．

視察によって，y=ax^2+b とします；

2a + 4(ax^2 +b) = x^2,

より，

2a +4b = 0, 4a =1.

これを解いて

a = 1/4, b = -a/2.

よって，強制解は

y = (x^2 - 1/2)/4.

これに自由解(同次解 : 初期条件を反映)を加えれば完全解になる．

〜〜〜〜 自由解は系統的に求め易い．

強制解は，なるべく簡単な解を探すしかない．自由解の線形和も選択肢のひとつ．今回の場合は，その場合でない．今回は，y = x^2 で考えても駄目なので，y = x^2 +b としてみた．

算術に慣れるのには「考える癖」が必要です．味噌は，「自分なりの考え」でどうしても解けないところまでいってから，答えを見て初めて「考える力」が進歩すると思います．

数学迷い人 さんのレス (2009/07/02(Thu) 17:56)

アドバイスありがとうございます．

強制解をつくるのは，y=e^(λx)と置くのは学んだのですが，決まりはなく何でも良いのでしょうか？１つではないのですよね？ 自由解の見つけ方も同上でしょうか？

また，No.24438に関して， y'-y=Dy-y=(D-1)yということですか？ そして，D=1より，e^x が作られました．これは，斉次の場合ですよね？ 今回は，右辺にsinxがあるので考慮するべきでしょうが，定数の場合は軽く触れたのですが，関数の場合のが，参考書で扱われていません．この微分方程式は，特別なのでしょうか？

何度も申し訳ございませんがお願いいたします．

mNeji さんのレス (2009/07/02(Thu) 22:09)

＞強制解をつくるのは，y=e^(λx)と置くのは学んだのですが，決まりはなく何でも良いのでしょうか？１つではないのですよね？ ＞自由解の見つけ方も同上でしょうか？

私は，微分方程式は演習をサボりにサボったので，本格的な説明ができません．ただ「y=e^(λx)」と置くのは，同次解(自由解)の求め方で，transferさんがNo.24438でお書きになっているご説明の通りだと思います．

他方，強制解(非同次解)の場合は，「強制」というだけ在って，色々な場合があるので，一概には言えません．「定数」だって一人前の強制力ですし，今回の場合でも，多項式，正弦関数，指数関数など様々ですね．一度，微分方程式の参考書をご覧になったら如何でしょうか．

正弦関数が強制項の場合は，計算の楽の為に，オイラーの公式を用いて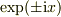， で表示し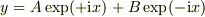， で展開するのも手ですよね．

指数関数 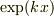が強制項の場合は，同次解(自由解)の求め方とどうようですが，「k」と「λ」が等しい場合は注意が必要です．

などと書いても，使わないと「指」が覚えてくれないので，参考書と演習で頑張ってください．

transfer さんのレス (2009/07/02(Thu) 22:59)

> y'-y=Dy-y=(D-1)yということですか？ > そして，D=1より，e^x が作られました．

はい，その通りです． 仮に，y'' + 2 y = D^2 y + 2 y = (D^2 + 2) y の場合，D^2 + 2 = 0=====＞D = ±i√2 ですから，この場合の基本解は，e^{i√2 x} と e^{- i√2 x} または sin √2 x と cos √2 x になります． つまり， y = C1 e^{i√2 x} + C2 e^{- i√2 x} または y = D1 sin √2 x + D2 cos √2 x となります． また，y''- 3 y'+ 2 y = (D^2 - 3 D + 2) y = (D - 2) (D - 1) y の場合， y = C1 e^{2 x} + C2 e^{x} が解になります．

> 斉次の場合ですよね？

非斉次（非同次）の場合は， y = e^x は解ではない，ということでしょうか？ 非斉次（非同次）の場合でも，一般解を構成するものです． (D - 1) y = sin x の斉次（同次）方程式は， (D - 1) y = 0 であり，これより，y = C e^{x} が得られました． (D - 1) y = sin x の場合は，C e^{x} に特解 f(x) を付け加えて， y = C e^{x} + f(x) が一般解になります． 演算子法の場合，特解は，逆演算子というもの（積分になります）で， f(x) = sin x / (D - 1) のようにして求めることもできます．（詳しくは演算子法が載っている微分方程式のテキストをご覧ください） なお，演算子法が適用できるのは，基本的に定数係数の線型微分方程式となります． 決して万能の処方ではありませんので，ご注意ください．

> この微分方程式は，特別なのでしょうか？

いえ，ごく普通の微分方程式です．

(2)の場合の特解は，f(x) = sin x / (D - 1) のようにして解く方法もある（テキストをご覧ください）のですが，素直にこれでやると面倒で， ここでは，f(x) = A sin x + B cos x と仮定して，未定係数の A, B を求める方が簡単です． つまり，問題を解く方法はいくつかありますが，どれが簡単かというと，一概には言えません．

素直な F(x) / (D - a) の計算(積分）の仕方

F(x) / (D - a) = e^{a x} ∫ e^{- a x} F(x) dx

このまま何も工夫せずに解くと一般に部分積分になりますが，その他，演算子・逆演算子での計算を楽にする有用な公式もテキストに数多く載っています．

ASA さんのレス (2009/07/03(Fri) 10:09)

> 演算子法の場合，特解は，逆演算子というもの（積分になります）で， > f(x) = sin x / (D - 1) のようにして求めることもできます． 今の場合なら，両辺にD+1を掛けて， (D^2-1)f=(D+1)sin x D^2f=-f:線型微分方程式の解ｆは線形でＡe^ixの形をしているから f=-1/2((D+1)sin x)=-1/2(cos x +sin x) と簡単にできますね．

ASA さんのレス (2009/07/03(Fri) 10:20)

'特'解fは'右辺の関数sin xの性質を反映して'線形でAe^ix に修正しておきます

ASA さんのレス (2009/07/03(Fri) 10:48)

(3)の特解も補足しておきます． (D^2+4)f=x^2ですから，左辺の関数は2冪なので，fはこの周辺の冪級数です． ちなみに(D^2+4)x^2=4x^2+2ですから， 係数合わせから，x^2の係数は，逆数1/4,定数項は,逆数1/2にx^2の係数1/4を掛けたものをキャンセルするから-符号をつけて，結果-1/8．

演算子法で特解にあたりをつける方法としては，左辺関数にオペレートして様子を見るというのがあります．

ASA さんのレス (2009/07/03(Fri) 11:48)

演算子法で正統なやり方も紹介しておきます． (3)1/(D^2+4)を分解して =1/8(1/(1+iD/2) +1/(1-iD/2)) 高次項を省略して(2次以上の項は，最終的に消えるため) =1/4 -D^2/16 x^2に作用させて，f=x^2/4-1/8

(2)も同様であるが，g=sin xはg''=-gを満たす関数のため特別 1/(D-1)=-1/(1-D) 高次省略(特別な理由より) =-(1＋D) sin xに作用させると h=-(sin x+cos x) しかし(D-1)h=2sin xとなるので 係数合わせを行い f=-(sin x+cos x)/2を得る．

積分でやるなら -1/(1-D)=-dx/(1-dx)=-(dx+dx^2+…) h=∫sinx-(dx+dx^2)を計算． 上の微分演算子と同様に係数合わせで最終調整を行う．

定数係数の線型微分方程式でも特解を求めるときには注意が必要ですな．

ASA さんのレス (2009/07/03(Fri) 13:02)

念ため，逆演算子1/(D-a)f=e^a∫e^(-a) fdx

fがe^bxならe^bx/(D-a)=e^bx/(b-a) つまｓり，D→bの置換が成立． sinx/(D-1)=im{e^ix/(D-1)}=im(1/(i-1)e^ix} 分母有理化 =-(1/2)Im{(1+i)(cosx+isinx)} =-(1/2)(cosx+sinx) なんにせよ，複雑な積分計算無しに求められます．

上記置換ルールとe^x/(D-1)=xe^x を覚えておくと便利かも．

mNeji さんのレス (2009/07/03(Fri) 13:45)

皆さん，

演算子法？，と言う感じで拝見していたのですが，ラプラス変換の事ですよね．公式を直ぐ忘れてしまうので，使い切れませんでしたが...，このスレッドを拝見しているうちに，ちょと思い出しました．

・ラプラス変換h ttp://www.tohtech.ac.jp/~comms/nakagawa/laplacetrans/Laplace1.htm

以前，このサイトを引用したものの，その良さを理解できていなかったようです(汗)．

ASA さんのレス (2009/07/03(Fri) 15:22)

mNejiさん 御紹介のサイトでは(D+1)^2y=sinxを例題にしてますね． 重解をもつケースでは，早速e^x/(D-1)=xe^xこの公式が役立ちます． y1=C1e^-xが例題の一つの解で，公式から(D+1)xe^-x=e^-x;(D,x)→(-D,-x) がわかるので直ちに，(D+1)^2 xe^-x=(D+1)e^-x=0 よってy2=C2xe^-x(定数変化法を使用しない) 特解は，No.24466の方法で(２回繰り返せばよい)から，f=-cosx/2とわかります．

ちなみにラプラス変換と演算子法はちょっと違います． ∫e^(-a) fdxこの部分のみをラプラス変換ですけど．

慣れの問題が大きいですが，定係数線型方程式の特解ならNo.24466当たりの方法が簡単と思います．

mNeji さんのレス (2009/07/03(Fri) 15:30)

ASAさん，

＞慣れの問題が大きいですが，定係数線型方程式の特解ならNo.24466当たりの方法が簡単と思います

この点はとても興味深いです．

No.24466の， ＞なんにせよ，複雑な積分計算無しに求められます．

ただ，まだご解説がすんなり理解出来ません．もし宜しければ，図書とかサイトをご紹介くださると，幸いです．

ASA さんのレス (2009/07/03(Fri) 15:51)

共立出版の詳解物理応用数学演習ぐらいしか知りません．

f=sinx/(D+1)^2だったら f=1/2i(e^ix-e^-ix)/(D+1)^2 とした方が簡単ですね．

=1/2i{e^ix/(i+1)^2-e^-ix/(-i+1)^2}:分母有理化 =1/2i(1/2^2){(-i+1)^2 e^ix-(i+1)^2e^-ix} =1/2i(1/2^2)(-2i) {e^ix + e^-ix} =-1/2 {cos x}

ほらね．ｓの部分分数展開に可能な形にもってく計算よりはるかに簡単でしょ．

ASA さんのレス (2009/07/03(Fri) 17:23)

微分方程式，演算子法でググッたらたくさんヒットしますね．

第2公式としては，{f/D-a}=e^x{fe^-x/D-a+1}を覚えた方が汎用性がありますね． f=e^x, a=1のケースで {e^x/D-1}=e^x{e^x*e^-x/D-1+1}=e^x{1/D}=e^x{x}=xe^x

(D^2+3D+2)y=(1+e^x)^(-1)などでは，上の公式を使用するといくらか簡単に解けます．

mNeji さんのレス (2009/07/03(Fri) 19:12)

＞微分方程式，演算子法でググッたらたくさんヒットしますね．

なんと面白い方法ですね．私は，「ときわ台学/微分方程式・特殊関数/演算子法」の解説に感動しました．ご教示を感謝します．

ASA さんのレス (2009/07/03(Fri) 19:55)

スレ主，数学迷い人さんのためには， ttp://www.tsuyama-ct.ac.jp/matsuda/d-eq/bi4.pdf このあたりが参考になるでしょう．

数学迷い人 さんのレス (2009/07/04(Sat) 18:17)

ありがとうございます．参考になります．僕にとっては，レベルの高い話ばかりで，とても苦戦していました．

今，微分演算子法について，学習を進めています．

ところで，質問の問題の，?の答えは，y=Ce^x -(sinx + cosx)/2 で合っていますか？定数変化法で解いたのですが，みなさん使われていないようなので，あまりお勧めできないとかですか・・・？ご検討よろしくお願いします．

また，特性方程式λ＾2+Pλ+Q＝0で，基本解が，複素数を含むとき， 例えば，λ＝-2（+-）iのとき， Ccosx + C'sinx となっていますが，オイラーの公式を使ってなりますか？ 丁寧にやっても，どちらの項にも，それぞれsinxとcosx両方が出てきちゃいます．

長くなってすみません．お願いします．

ASA さんのレス (2009/07/04(Sat) 19:37)

数学迷い人さん

No.24458で求めた特解と一致しているので，あっていると思います． どんな方法でも解ければいいので，定数変化法で十分でしょう． なんにせよ，使いこなせることが最重要だと考えます． しかし，演算子法だと，前に紹介したような特定のケースで，かなり簡単に求めることもできます(試験問題などでは該当ケースである場合が多い)． 計算ミスも少なくできるので，知っていて損ではないはずです．

>Ccosx + C'sinx となっていますが，オイラーの公式を使ってなりますか 特性根が，純虚数ならそうですが，一般の複素数のときはそうなりません． λ＾2+2pλ+q＝0, λ=p(+-)√(p^2 -q) p≠0かつp^2-q<0なら 複素数で，このときp^2-q=-r^2とおいて y=(Ccos(rx) + C'sin(rx))e^px となるはずです．

mNeji さんのレス (2009/07/04(Sat) 20:06)

?y'-y=sinx について，一例として，私の考え方を参考として書いてみます．

〜〜〜〜復習〜〜〜〜 線形微分方程式の一般解，yを自由解f(x)と強制解g(x)とに分けて考えます； y(x) = f(x) + g(x).(1)

ここで，自由解f(x)は，微分方程式； f'-f = 0, (2) を満たすと同時に，初期条件y(0)を満たす； f(0) = y(0). (3)

強制解g(x)は，微分方程式； g'-g = sin(x), (4) を満たすと同時に，初期条件0を満たす； g(0) = 0. (5)

式(2),(4)を辺々加えると，式(1)は，問題の微分方程式を満たす事がわかる．また，式(3),(5)を加えると，式(1)の初期条件も当然満たします．

自由解は，直接積分して求める事も可能でしょうし，特性方程式によって求めてもいいですね．

そこで強制解は，是非とも演算子法の練習とおもって自分で解いてみて下さい．間違っても良いから，自分の指で出来るとこまでやって見て下さい．

〜〜〜〜強制解のごり押し法〜〜〜〜 以下では，オイラーの公式でごり押しする方法をやって見ます．

まず式(4)の右辺にオイラーの公式を適応して，

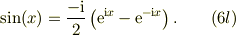
他方左辺で，次に展開出来ると仮定し てみます，

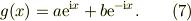
すると，式(4)の左辺は，

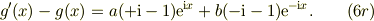
式(6r)と式(6l)は等しいのだから，

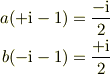
明らかに「bはaの複素共役: 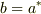」だから，aを解くだけでいいので；

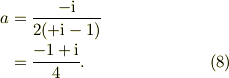
この時，

〜〜〜〜 とにもかくにも，特解は解ければいいので，色々な技法に触れて置けばいいのでしょうね．確かに演算子法は，逆関数の求め方がスマートですね．

transfer さんのレス (2009/07/05(Sun) 00:22)

> ?の答えは，y=Ce^x -(sinx + cosx)/2 で合っていますか？

定数変化法だと，y = C(x) e^{x} のようにして， C' e^{x} = sin x を解けばいいわけですが， y = C e^{x} - (sin x + cos x) / 2 で合っています． y = A sin x + B cos x と仮定して，A, B を求めても同じです． 要は自分の好きな方法で正しく求められればいいだけです． 演算子法にこだわる必要はありません．

> 例えば，λ＝-2（+-）iのとき，

この場合は，次のようになります．（C1, C2 は実数定数） y = e^{- 2 x} (C1 cos x + C2 sin x)

仮に，λ = - 3 ± i √5 なら， y = e^{- 3 x} (C1 cos √5 x + C2 sin √5 x) となります．

数学迷い人 さんのレス (2009/07/05(Sun) 10:26)

ありがとうございます．合ってて安心しました．

ところで，> 例えば，λ＝-2（+-）iのとき，

この場合は，次のようになります．（C1, C2 は実数定数） y = e^{- 2 x} (C1 cos x + C2 sin x)

仮に，λ = - 3 ± i √5 なら， y = e^{- 3 x} (C1 cos √5 x + C2 sin √5 x) となります．

とありますが，どのように変換していますか？ オイラーの公式だけでは導けません．．．

ASA さんのレス (2009/07/05(Sun) 11:23)

迷ってますね．

特性根をλ1,λ2とすると 自由解は，A,B;任意定数として y=Ae^(λ1x) + Be^(λ2x)となります． 計算問題ならここでお終りでかまいません．

仮に，λ1=-p+ir,λ2=-p-ir;(p,r;実数)なら，共通因子e^-pxを括りだし， y=e^-px {Ae^irx +Be^-irx} ここでe^irxとe^-irxにオイラー公式を適用(A,Bには適用しない)． 最後の仕上げで，C1=(A+B),C2=(A-B)へと整理することも可能です． {A,B}，{C1,C2}ともに，任意定数で，初期条件に合うように微分最高次数と同じく2つでペアになってます． ここでyを実解に限定すれば，それぞれ，実定数ペアとなります． 実定数ペアの表現としては，{α,δ}を使い，αsin(rx+δ)等の形にすることもあります(波としての振幅と位相)．

がんばってください．

transfer さんのレス (2009/07/05(Sun) 18:40)

指数関数の性質です． e^{a + b} = e^{a} e^{b}