Diracのデルタ関数
Diracのデルタ関数
トビラ.. さんの書込 (2009/06/29(Mon) 23:18)
こんばんは,ディラックのデルタ関数についての質問なのですが本によると,( 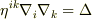 と定義し,
と定義し, 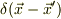 をDiracのデルタ関数とします.)
をDiracのデルタ関数とします.)
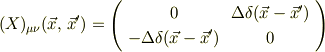
の逆行列は
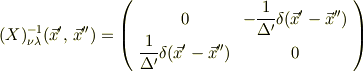
となっているのですが,どうしてこうなるのでしょうか?僕が計算すると
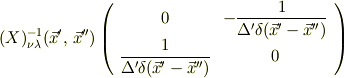
となるんです. どうしてもわからないので,アドバイスお願いします.
Re: Diracのデルタ関数
mNeji さんのレス (2009/06/30(Tue) 14:25)
また茶々ですが....最近,すこしテンソルの算数に興味をもってちょこちょこしているので,こんな計算がどこからで出て来るのだろうか,と思う次第です.二次元の重力波の問題でグリーン関数の積分でもするのだろうかと....
もしよければ,問題の背景を優しくお教え下さいませんか?
Re: Diracのデルタ関数
toorisugari no Hiro さんのレス (2009/06/30(Tue) 19:57)
4x4の対角行列
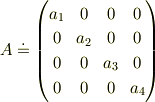
つまり,
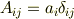
の逆行列は 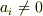 なら存在して
なら存在して
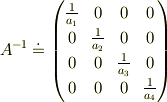
つまり,
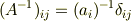
であって
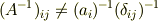
です.
# 後者だと行列要素の非対角成分に1/0が現れてしまいます.
# 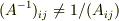 ですよね.そもそも.
ですよね.そもそも.
当然積は
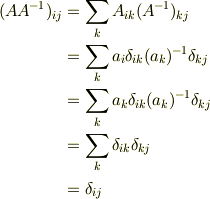
と単位行列になる.
δ関数でもおなじ事.有限次元のベクトル空間だろうが,無限次元のベクトル空間だろうが対角行列の逆は対角行列.
Re: Diracのデルタ関数
トビラ.. さんのレス (2009/07/01(Wed) 01:30)
mNejiさんtoorisugarino Hiroさん回答どうもありがとうございました.
mNejiさんへ これだけを見ただけで重力波とつながりがあると思うなんて鋭いですね. 僕は重力場の正準量子化を勉強しようとしてたら,Diracの括弧の使い方を学んで,それを電磁場に応用しようとしてつまずいたんです.ガボーン
toorisugarino Hiroさんへ
デヘヘとてもわかりやすい解説ありがとうございました.
僕はDiracのデルタとデルタ関数の関係がごちゃごちゃでした.
ただ,やっぱり少し気になるのですが,このデルタ関数の前にはラプラシアンがありそのラプラシアンはデルタ関数に作用しているんです.その場合でもそのようなことが許されるのでしょうか?ラプラシアンが作用するとデルタ関数の性質を維持できないようなできるような・・・そのあたりがよくわからないんです.
mNejiさんの要望もあり,一応この式 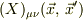 の行列に至った経緯を載せておきます.
の行列に至った経緯を載せておきます.
まず,電磁場の4元ポテンシャルを 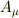 とします.それに正準共役なものを
とします.それに正準共役なものを 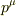 で定義します.ここでは,ラテン字
で定義します.ここでは,ラテン字 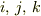 などは1〜3までを示し,ギリシャ字
などは1〜3までを示し,ギリシャ字 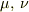 は1〜4までを示すものとします.また,上下に同じ指標が現れた場合,合計をとるものとします.
ここで,Poissonの括弧を次のように定義します.
は1〜4までを示すものとします.また,上下に同じ指標が現れた場合,合計をとるものとします.
ここで,Poissonの括弧を次のように定義します.
![[C,\,D]=\int \left( \frac{\delta C}{\delta A_\mu}\frac{\delta D}{\delta p^\mu}-\frac{\delta D}{\delta A_\mu}\frac{\delta C}{\delta p^\mu}\right)d^3x](http://hooktail.maxwell.jp/bbslog/d04d65474559a8962438be7a193b21bd.png)
上述の右辺に現れる 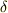 は変分を意味するものとします.
また,
は変分を意味するものとします.
また, 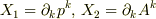 とします.
とします.
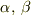 に関しては1と2をあらわすものとします.
に関しては1と2をあらわすものとします.
![(X)_{\alpha,\,\beta}(x,\,x^\prime)=\left([ X_\alpha(x) ,\,X_\beta (x^\prime)]\right)=\left(\begin{array}{cc}[X_1,\, X_1]&[X_1,\, X_2]\\. [X_2,\,X_1] &[X_2,\, X_2]\end{array}\right)](http://hooktail.maxwell.jp/bbslog/4ef3c356368b422807e375475bb8d9b0.png)
この右辺の 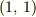 成分と
成分と 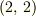 成分はPoissonの括弧の対称性
成分はPoissonの括弧の対称性 ![[A,\,B]=-[B,\,A]](http://hooktail.maxwell.jp/bbslog/3cf29560b313376d401bf855d4f86ee6.png) より0になります.
より0になります.
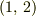 成分は
成分は
![(X)_{1,\,2}(x,\,x^\prime)=[X_1(x),\,X_2(x^\prime)]=\int \left( \frac{\delta X_1(x)}{\delta A_\mu(x^{\prime\prime})}\frac{\delta X_2(x^\prime)}{\delta p^\mu(x^\prime\prime)}-\frac{\delta X_2(x^\prime)}{\delta A_1(x^{\prime\prime})}\frac{\delta X_1(x)}{\delta p^\mu(x^\prime\prime)}\right)d^3x^{\prime\prime}](http://hooktail.maxwell.jp/bbslog/44965ad5094e8bbdac0ccef64b9763d2.png)
この式に先ほどの 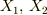 を代入して
を代入して
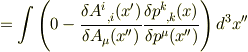
ここで,オイラーラグランジュの方程式を使い
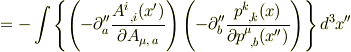
ここで,部分積分をつかい
![=-\int \left[ \partial^{\prime\prime} _b\left\{ \partial^{\prime\prime} _a\left(\frac{\partial A^i_{\,\,\, ,i}(x^\prime)}{\partial A_{\mu,\, a}(x^{\prime\prime})}\right) \delta ^k_\mu\delta ^b_k\delta (x-x^{\prime\prime})\right\}\right]d^3x^{\prime\prime}+\int \left[ \left\{ \partial^{\prime\prime} _b \partial^{\prime\prime} _a\left(\frac{\partial A^i_{\,\,\, ,i}(x^\prime)}{\partial A_{\mu,\, a}(x^{\prime\prime})}\right)\right\} \delta ^k_\mu\delta ^b_k\delta (x-x^{\prime\prime})\right]d^3x^{\prime\prime}](http://hooktail.maxwell.jp/bbslog/a30fee64485158c9e20ae20824317ac5.png)
この第1項は境界で0となるので,第2項の積分を実行すると
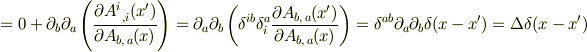
というわけで,このラプラシアンはDiracのデルタ関数に作用しているわけです(多分) それとtoorisugarino Hiroさんの話を聞く限りではこの場合単位行列って
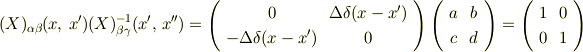
ではなく,
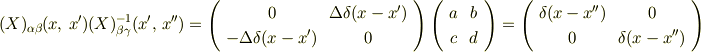
となるんでしょうか? そうなると上述の関係式をといて,
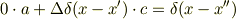
なので, 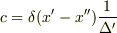 とおくと上述の式の左辺にこの
とおくと上述の式の左辺にこの  を代入して
を代入して
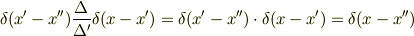
となって右辺と一致するのでしょうか? そう考えればなんか納得いく気がします.たぶん,いまいったことはtoorisugari noHiroさんの言っていることをデルタ関数に置き換えただけなんだろうけども,とにかく理解できた気がします.(多分) でも間違っていたら指摘してください. 本当にありがとうございました.とてつもなくすっきり爽快です. (なんか,これ↑を書いていくうちにとけた,スミマセン)
Re: Diracのデルタ関数
toorisugari no Hiro さんのレス (2009/07/01(Wed) 10:29)
> 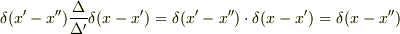
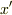 での積分を忘れていますよ.
での積分を忘れていますよ.
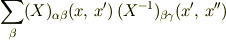
でなく,
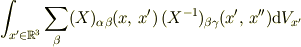
としないと「行列」の乗算になりませんよ. もちろん結果は
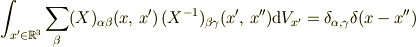
です.
Re: Diracのデルタ関数
mNeji さんのレス (2009/07/01(Wed) 10:49)
再度,茶々です.最近,サッカーの練習方法の解説書が出て,『ポルトガルの研究者が30年ほど前に発案した"Periodization Tactica"に沿ってサッカーの強化法を見直す試み.』が論じられています.そこでスペインに於けるサッカーの上手さの一つに「ストリート・サッカー」と「週末でのリーグ戦」とがあげられていました.
門前の小僧の立場からすると,トビラ..さんの質疑応答は見ているだけでもとても刺激的で,「ストリート・サッカー」ならぬ「ストリート論戦」を拝見させていただいているから興味深いのだと思いました.
いつの日か,自分も直接に論議に加わりたい者です(笑).
Re: Diracのデルタ関数
toorisugari no Hiro さんのレス (2009/07/01(Wed) 14:35)
>> 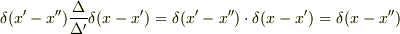 >
> 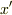 での積分を忘れていますよ.
での積分を忘れていますよ.
Laplacianは微分演算子であって,数ではないので,本来は簡単に交換できません.まじめに計算すると結構大変です. 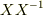 の
の 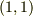 成分は
成分は
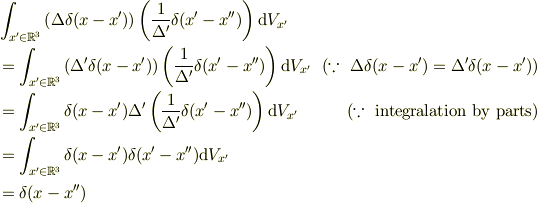
となります.
Re: Diracのデルタ関数
トビラ.. さんのレス (2009/07/01(Wed) 23:35)
> 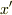 での積分を忘れていますよ.
での積分を忘れていますよ.
・・・そ,それは知りませんでした.行列の乗算は多分経験ないです.
>トビラ..さんの質疑応答は見ているだけでもとても刺激的で,「ストリート・サッカー」ならぬ「ストリート論戦」を拝見させていただいているから興味深いのだと思いました
グヘヘ・・・なんかよくわかんないけど嬉しいです(笑)・・・ありがとうございます. デヘヘ
>Laplacianは微分演算子であって,数ではないので,本来は簡単に交換できません.まともに計算すると結構大変です
ふむふむ,この式の上から3行目の式でラプラシアンが右のデルタ関数に作用していますけど,これは単純に2回部分積分したと考えればいいのでしょうか?(英語苦手だからいんてぐられーしょんぱーてす?の意味がわかんなかった.) もう一つお聞きしたいのですが,汎関数微分と変分の関係についてなのですが, 今すぐ頑張って式書くのでできれば答えてくれれば助かります.
Re: Diracのデルタ関数
トビラ.. さんのレス (2009/07/02(Thu) 00:00)
すみません嘘こきました.汎関数微分のことについてお聞きしようと思ったんですけど今考えていたら問題解決しました.スミマセン
Re: Diracのデルタ関数
toorisugari no Hiro さんのレス (2009/07/02(Thu) 10:12)
> ・・・そ,それは知りませんでした.行列の乗算は多分経験ないです.
この行列 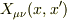 は引数
は引数 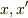 を持つ関数を要素とする,添字が
を持つ関数を要素とする,添字が 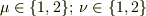 である2x2行列とみることもできますが,
今回は添字が
である2x2行列とみることもできますが,
今回は添字が 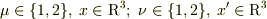 となる「行列」と考えているようです.(背景を良く理解していないので,なぜ,そのように考えるかはわかりません.)
この世界での単位行列は
となる「行列」と考えているようです.(背景を良く理解していないので,なぜ,そのように考えるかはわかりません.)
この世界での単位行列は 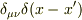 になります.
になります.
> 単純に2回部分積分したと考えればいいのでしょうか?
そうです.あるいはLaplacianはエルミート演算子だからと理解してもらっても結構です.
Re: Diracのデルタ関数
mNeji さんのレス (2009/07/02(Thu) 11:07)
今回の論議が素人目に興味深いのは,「  vec x-vec x^prime|7215ee9c7d9dc229d2921a40e899ec5f| 」のように,本当に場所の違う2点での座標(?)らしい量が出て来る事,だと感じます.やはり,何かが2点間を伝搬して欲しいです.
vec x-vec x^prime|7215ee9c7d9dc229d2921a40e899ec5f| 」のように,本当に場所の違う2点での座標(?)らしい量が出て来る事,だと感じます.やはり,何かが2点間を伝搬して欲しいです.
その上, >> 単純に2回部分積分したと考えればいいのでしょうか? >そうです.あるいはLaplacianはエルミート演算子だからと理解してもらっても結構です.
なんて,何処かで聴いた様なセリフまで拝見して,面白さが加速しました.
Re: Diracのデルタ関数
トビラ.. さんのレス (2009/07/02(Thu) 13:58)
>この世界での単位行列は, 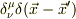 です.
です.
なるほど,ただ少し気になるのは, 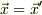 の場合単位行列の対角成分が無限大になってしまうのが少しふに落ちないです.(それ以外の成分も
の場合単位行列の対角成分が無限大になってしまうのが少しふに落ちないです.(それ以外の成分も 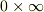 となって不定型になる気もします.)これはこの行列を全空間で積分してデルタ関数が消えることを見越しているのでしょうか?
となって不定型になる気もします.)これはこの行列を全空間で積分してデルタ関数が消えることを見越しているのでしょうか?
あと,正準変数を 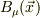 とすると,
とすると, 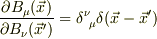 となると解釈すると今読んでいる本の内容がとても納得いくのですが,この式はただしいのでしょか?正しいとすれば,どうしてこのようになるのでしょうか?
本当に疑問符ばかりで申し訳ないです.僕も一応解析力学などの本で調べてみたりはしたのですがなかなかこのことについて触れている本が見当たりませんでした.
何かお勧めの本があれば,紹介していただけると幸いです.
となると解釈すると今読んでいる本の内容がとても納得いくのですが,この式はただしいのでしょか?正しいとすれば,どうしてこのようになるのでしょうか?
本当に疑問符ばかりで申し訳ないです.僕も一応解析力学などの本で調べてみたりはしたのですがなかなかこのことについて触れている本が見当たりませんでした.
何かお勧めの本があれば,紹介していただけると幸いです.
>なんて,何処かで聴いた様なセリフまで拝見して,面白さが加速しました.
もしかして,前にも同じこと僕言いました?(笑)
Re: Diracのデルタ関数
mNeji さんのレス (2009/07/02(Thu) 14:28)
>もしかして,前にも同じこと僕言いました?(笑)
いえ違います.こんな別世界でも知った単語に会えたなー,という単純な話です(爆).
Re: Diracのデルタ関数
トビラ.. さんのレス (2009/07/02(Thu) 18:08)
そういう意味でしたか. 僕は量子力学学んだことないのでそろそろ量子力学を学ぼうかなーて思ってます(今さらかよ!ガボーン)
なので僕から見ればmNejiさんや皆さんの方がETです!笑
次に読もうと思っている本はキーポイント量子力学って本なんですけど,他におすすめの本がありましたら教えてくださるとたすかります. 僕は量子力学は詳しく学ぼうとは思っていないので,応用などはあまり載っていない方がいいです.重要な公式を省かず,きちんと,そして自然な流れで,分かりやすく導出している本がいいです.(めっちゃ贅沢)
そんな本がありましたら教えてくださると助かります.
Re: Diracのデルタ関数
toorisugari no Hiro さんのレス (2009/07/02(Thu) 19:14)
> なるほど,ただ少し気になるのは, 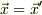 の場合単位行列の対角成分が無限大になってしまうのが少しふに落ちないです.(それ以外の成分も
の場合単位行列の対角成分が無限大になってしまうのが少しふに落ちないです.(それ以外の成分も 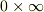 となって不定型になる気もします.)これはこの行列を全空間で積分してデルタ関数が消えることを見越しているのでしょうか?
となって不定型になる気もします.)これはこの行列を全空間で積分してデルタ関数が消えることを見越しているのでしょうか?
離散的な添え字は理解できても,連続な添え字は理解しづらいものです.でも,連続変数の離散近似で考えればよいです.
空間を碁盤の目のように離散的に考えます. 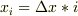 連続な添え字
連続な添え字 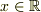 を離散的な添え字
を離散的な添え字 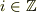 にするわけです.
にするわけです.
> |90cab27f56330d9b0297ff1d27f39583| となると解釈すると今読んでいる本の内容がとても納得いくのですが,この式はただしいのでしょか?正しいとすれば,どうしてこのようになるのでしょうか?
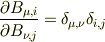
は理解できますか?本質的に同じです.
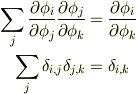
ですから,同じ関係
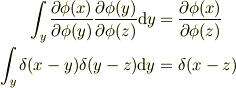
が成り立つように定義したと考えては?
汎関数微分とは, 離散的な添え字に対する偏微分
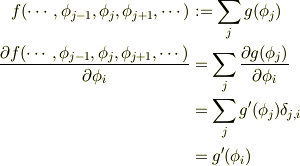
を連続的な添え字の「偏微分」
![f[\phi] &:= \int g(\phi(y))dy\\\frac{\delta f[\phi]}{\delta \phi(x)} &= \int \frac{\partial g(\phi(y))}{\partial \phi(x)}dy\\&= \int g'(\phi(y))\delta(y-x)dy\\&= g'(\phi(x))](http://hooktail.maxwell.jp/bbslog/da9477fa15d3f6d9c574f41b86d1b504.png)
に拡張したものに過ぎません.
Re: Diracのデルタ関数
mNeji さんのレス (2009/07/02(Thu) 23:43)
>そんな本がありましたら教えてくださると助かります.
そんな本は,toorisugari no Hiroさんにご紹介戴くの良いでしょう.
私の場合,近くの区の図書館にある唯一の量子力学の教科書が;
物理学ライブラリ−7,8 量子力学I, II 著者名 高田 健次郎・著 出版社 東京朝倉書店 出版年月 1983-02,04
です.最近,量子力学の質問がちょこちょこあるので借用していますが,結構要領よく書かれているようです.
他方,入門書ですが,自分が電磁気の本として勉強させて頂いた砂川さんの;
書名 量子力学の考え方 著者名 砂川重信著 出版社 東京岩波書店 出版年月1993-07
は,ゆったりと説明しています.自分が学生の時に出ていたら,もうすこし量子力学が好きになっていたかも知れません.
Re: Diracのデルタ関数
トビラ.. さんのレス (2009/07/03(Fri) 00:04)
toorisugari no hiroさんどうもありがとうございます.とても感謝しています.
>連続変数の離散近似で考えればよいです.
ありがとうございます.この助言がなければクロネッカーのデルタとデルタ関数の性質が等しいことが証明できませんでした. 証明してみたんですけども,この証明で正しいでしょうか?(自信はあります)
まず,離散近似を考えます. 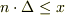 <
< 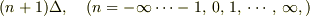 とします.
とします.
・ 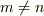 の場合
クロネッカーのデルタは
の場合
クロネッカーのデルタは
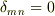
となります. 離散近似を用いた場合のデルタ関数は
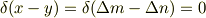
となってこの場合 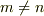 はデルタ関数とクロネッカーのデルタは等しく0となります.
はデルタ関数とクロネッカーのデルタは等しく0となります.
・ 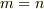 の場合
クロネッカーのデルタは
の場合
クロネッカーのデルタは
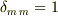
となります.(ただし,ここでは 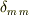 は
は 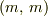 成分をあらわすのであって合計
成分をあらわすのであって合計 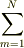 をとるものではないとします.)
離散近似を用いたデルタ関数は
をとるものではないとします.)
離散近似を用いたデルタ関数は
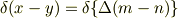
ですが,ここで注意しなくてはならないのが最小単位が 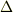 である以上,例え
である以上,例え 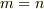 であっても,そこには
であっても,そこには 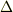 の大きさがあります.したがって,この微小領域
の大きさがあります.したがって,この微小領域 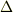 での面積(?)が1であればクロネッカーのデルタ一致すると考えて問題ないということになります.今までは離散変数を考えてきましたが,ここで連続変数
での面積(?)が1であればクロネッカーのデルタ一致すると考えて問題ないということになります.今までは離散変数を考えてきましたが,ここで連続変数  を導入します.そして,
を導入します.そして, 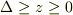 とします.つまり,この連続な
とします.つまり,この連続な  は領域
は領域 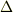 の中の物差しともいえます.よって
の中の物差しともいえます.よって 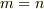 の場合,このデルタ関数は正確には
の場合,このデルタ関数は正確には 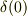 ではなく
ではなく 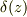 とすることが許されるはずです.したがってこの領域の面積(体積)は
離散近似で
とすることが許されるはずです.したがってこの領域の面積(体積)は
離散近似で
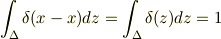
となって,この場合でもクロネッカーのデルタとデルタ関数が等しくなり無矛盾であることが証明できます.
また,ここでは離散近似を用いたデルタ関数とクロネッカーのデルタが同じ性質を持っていることを証明しましたが,ここで考えた離散近似を用いたデルタ関数の極限値を考えると,つまり, 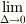 が一般に用いられるデルタ関数であると解釈でき,デルタ関数とクロネッカーのデルタの性質(?)が同じであると証明できたことになります.
が一般に用いられるデルタ関数であると解釈でき,デルタ関数とクロネッカーのデルタの性質(?)が同じであると証明できたことになります.
という証明でよろしいでしょうか?
Re: Diracのデルタ関数
toorisugari no Hiro さんのレス (2009/07/03(Fri) 13:06)
近似の仕方が違うように思います.
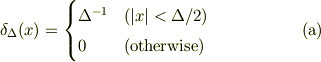
なら
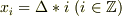 に対して
に対して
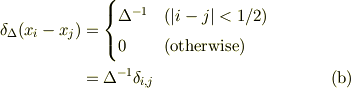
となります.
なお,近似(a)は任意の連続関数  に対して,
に対して,
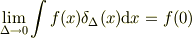
つまり
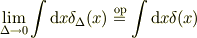
を満たします.
Re: Diracのデルタ関数
トビラ.. さんのレス (2009/07/04(Sat) 01:56)
確かに僕の近似の仕方はおかしかったですね. toorisugari no Hiroさんの解答を参考に,一応前に載せた近似の修正をしてみました.
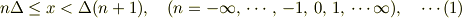
とおいて,近似的に 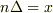 とします.これは,上述の式より
とします.これは,上述の式より 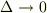 の極限で完全に
の極限で完全に  と一致すると考えれらます.
と一致すると考えれらます.
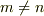 の場合
の場合
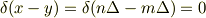
とDiracのデルタ関数の性質によりなります.
次に
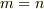 の場合
これは,近似的に
の場合
これは,近似的に
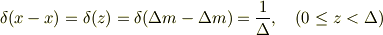
と置きます.(この  は唯一連続変数とします.
は唯一連続変数とします. 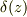 となっているのは式
となっているのは式 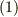 のため)この関係式は
のため)この関係式は 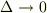 で左辺も本来の連続変数に戻り(
で左辺も本来の連続変数に戻り( 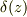 も
も 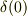 になる),右辺も無限になってこの条件ではデルタ関数の性質が成立することが理解できます.
になる),右辺も無限になってこの条件ではデルタ関数の性質が成立することが理解できます.
上述の2つの場合をまとめると,この離散近似でのデルタ関数とクロネッカーのデルタとの関係式が導かれ
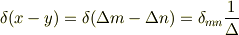
となります.両辺に 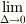 をつけるとこの極限において等しくなると思います.(ただ,
をつけるとこの極限において等しくなると思います.(ただ, 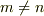 の場合,右辺が
の場合,右辺が 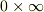 となって不定関数になりそうな気はするが・・・)
この離散近似を用いたデルタ関数の発散の仕方も,toorisugari no Hiroさんと同じ計算により1となって連続変数のデルタ関数の発散の仕方と同じであることが証明できると思います.
となって不定関数になりそうな気はするが・・・)
この離散近似を用いたデルタ関数の発散の仕方も,toorisugari no Hiroさんと同じ計算により1となって連続変数のデルタ関数の発散の仕方と同じであることが証明できると思います.
と,一応前回の自分の間違えを修正してみました.(今度こそ多分大丈夫,汗)
mNejiさんへ
紹介してくれた量子力学の本
>物理学ライブラリ−7,8 量子力学I, II 著者名 高田 健次郎・著 出版社 東京朝倉書店 出版年月 1983-02,04
をぱっとですが見てみました.数式の横にわかりやすく数式の名前(?)や意味を書いていてmNejiさんの言うようにまとめられている本だとおもいました.一ヶ月くらいで量子力学を学ぼうと思っていたけど,この本の厚さをみると,自分の考えが浅はかだったと考えずにはいられないです.(しかもこの分厚い本2冊もあるし・・・) 公式の証明に力を入れたいので,ほかにも振一郎さんの量子力学の本も評判いいようなので両方見ながら量子力学の公式の証明に頑張ろうかなって思っています.どちらの本も分厚くその上2冊ずつあるので(汗)重要な公式の証明だけを抜き出して勉強する「つもり」です.多分この考えも浅はかだと思います.
Re: Diracのデルタ関数
toorisugari no Hiro さんのレス (2009/07/04(Sat) 16:07)
表記が紛らわしいですが,たぶん,よいとおもいます.
>(ただ, 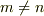 の場合,右辺が
の場合,右辺が 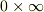 となって不定関数になりそうな気はするが・・・)
となって不定関数になりそうな気はするが・・・)
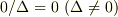 より
より
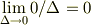
でしょ. 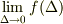 は
は 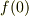 とは違う概念ですよね.
とは違う概念ですよね.
Re: Diracのデルタ関数
トビラ.. さんのレス (2009/07/04(Sat) 17:41)
やっと,やっといいと言われた.(汗) toorisugari no hiroさんの数学力には驚かされます.いつかtoorisugari no Hiroさんのようになりたいです.
>表記が紛らわしいです
ごめんなさい気がきかなくて.
>とは違うものですよね.
そうでした.聞いてみれば理解できるけど,自分ではその証明できなかった.(苦笑)
今回も大変お世話になりました.どうもありがとうございました. (次回もよろしくお願いします.ボソッ・・・)