Coo さんの書込 (2009/06/29(Mon) 13:59)

半径 a[m]の内部導体球を，内半径 b[m]，外半径 c[m]の中空導体で包み， 中空導体を接地し，内部導体球に＋Q[C]の電荷を与えた場合，中空導体外， 中空導体表面，内部導体球それぞれの電位を求めよ．

↑のような問題なんですが，問題だけあって答えなどが無いので，解けません．

問題集などを探してみると，内部導体球に+Q[C]を与えた場合の電位を求める問題があり， 中央の+Qによって，中空導体の内側に-Q，外側に+Qが帯電することから，中空導体外と，内部導体球と中空導体の間(a〜b)は，+Qとなるので， E=Q/4πε0r^2となり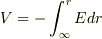， でやっていました．

これと，最初の問題では，外側を接地すると書いてあるので，同じように出来ない なとは思ったんですが，どうすればいいんでしょうか？ あと，問題集の方で考えたとき，内部導体球の電位は単純に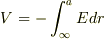， とやってかまわないのでしょうか？ それとも，∞〜cまでの積分から，c〜aを引けばよいのでしょうか？

mNeji さんのレス (2009/06/29(Mon) 18:24)

Cooさん，初めまして．

外側の球(球B)は，内径bより内側が空虚で，内径bから外径cまで金属が充填されているのでしょうか？そして，外径aの金属球(球A)に電荷+Qをチャージして，外径cの金属を接地するのでしょうか？

もしそうなら，球Aの電荷の逆の電荷「-Q」が球Bの内側に静電誘導を起こし，そのまた逆の電荷「+Q」が球Bの外側に誘導されるものの，接地されているので，この球Bの外側に誘導される電荷，「+Q」は接地側の彼方に流れ出てしまうと考えていいとおもいます．

という事は，球Aの表面電荷と球Bの内側表面電荷だけで，電場が決まりますね．また，電位は，状況が変わっても電位が変動し難いと思われるところを基準に考えれば良いのでしょう．ですから，接地先の電位から見て電位を計算すれば十分だと思います．

Coo さんのレス (2009/06/29(Mon) 19:03)

mNejiさん，初めまして．

問題文をそのまま載せたので，形は，多分そうだとしかいえないのですが…… 結局のところ，球Aの表面と外側の球Bの内側表面でコンデンサのような形になっていると考えればいいということでしょうか？

解説で，接地されている状態の考え方は分かったのですが， 「電位は，状況が変わっても電位が変動し難いと思われるところを基準に考えれば良いのでしょう．ですから，接地先の電位から見て電位を計算すれば十分だと思います．」 というのが，ちょっと分かりません．

あと，中空導体球外(r > c)の電界を調べる時に，ガウスの定理に当てはめる場合，Qは＋Qと−Qで消えてしまうと考えて，0としてしまっていいのでしょうか？

mNeji さんのレス (2009/06/29(Mon) 19:47)

＞結局のところ，球Aの表面と外側の球Bの内側表面でコンデンサのような形になっていると考えればいいということでしょうか？

と，思います．

＞というのが，ちょっと分かりません．

ちょっと，ジョーク交じりです．大昔，「接地」とは何かで悩んでいたので接地とは，ちょっとやそっとの電荷が流入しようが，流出しようが電位が変わらない様な物体と理解すれば良いと，言いたい訳です．

さて，すこし解り易くいえば，接地の電位をゼロとします．当然，接地と球Bを繋いでいる電線には電位勾配がありませんから，球Bの表面から半径bの内側表面までは等電位になります．仮に電位差があるとすると，球Bと接地との間に電流をしょうじてしまいます．

従って，球Bの内径bから球Aの表面までの電場の積分をする必要が生じます．

＞あと，中空導体球外(r > c)の電界を調べる時に，ガウスの定理に当てはめる場合，Qは＋Qと−Qで消えてしまうと考えて，0としてしまっていいのでしょうか？

そうですね．正確にいえば，(r > c)の領域には，他の電荷が無い限りはそうだと言えます．

電荷がクーロンの法則に従ってくれる限り，球対称の分布が明らかであれば，考察点の半径よりも外側の電荷分布が考察点での電場に寄与しないというのは面白いですよね．