スピンの合成
スピンの合成
hibikaisou さんの書込 (2009/06/28(Sun) 13:41)
はじめまして,質問です.
スピン1/2の粒子aとスピン1の粒子bを考える.
それぞれのスピン角運動量演算子を,Sa,Sbとする.
このときSa・Sbについて,すべての固有状態と固有ベクトルを求めよ.
という問題なんですが,
S=Sa+Sbとすると,
Sa・Sb= 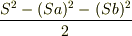 ここで
ここで  ,
, 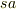 ,
, 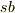 (小文字のs)を
それぞれS,Sa,Sbの固有値とすると…
固有値は
(小文字のs)を
それぞれS,Sa,Sbの固有値とすると…
固有値は 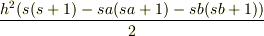 ですよね?
今sa=1/2,sb=1なのでs=-1/2,-3/2,1/2,3/2の4つだから,
Sa・Sbの固有値は
ですよね?
今sa=1/2,sb=1なのでs=-1/2,-3/2,1/2,3/2の4つだから,
Sa・Sbの固有値は 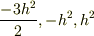 であってますか??
次に固有状態ですが,Sa・Sbの固有状態は
であってますか??
次に固有状態ですが,Sa・Sbの固有状態は 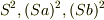 の固有状態と同じものですか?チンプンカンプンのこと言ってたらすいません.
の固有状態と同じものですか?チンプンカンプンのこと言ってたらすいません.
Re: スピンの合成
mNeji さんのレス (2009/06/28(Sun) 16:51)
hibikaisouさん,初めまして.
いわゆる「角運動量の合成」問題ですね.真っ当に説明すると,とても難しいので,詳しくは量子力学や物理数学の群論などの解説を読まれる事をお勧めします.
さて,今回は異なる粒子間のスピンの合成が問題のようですが,例えば,水素原子での電子が持つスピンと,電子の軌道角運動量との全角運動量などの場合もあります.これらは,数学的に「クレブッシュ-ゴルダン係数」という形で角運動量の合成規則としてまとめられるので,安心してくだいさい(笑).
今の場合,粒子1の角運動量演算子を, 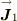 ,そのうち,ある座標方向(仮にz軸)の 角運動量射影演算子を,
,そのうち,ある座標方向(仮にz軸)の 角運動量射影演算子を, 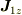 としたとき,この粒子1の角運動量の状態は,角運動量演算子の自乗の値と角運動量射影演算子の値とが,同時に固有状態となることが知られています;
としたとき,この粒子1の角運動量の状態は,角運動量演算子の自乗の値と角運動量射影演算子の値とが,同時に固有状態となることが知られています;
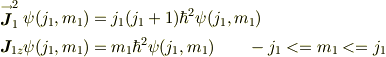
ここで, 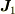 は,いわゆるベクトル演算子で,
は,いわゆるベクトル演算子で, 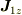 はスカラー演算子です.ですから丁寧に書けば;
はスカラー演算子です.ですから丁寧に書けば;
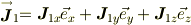
同様な事が粒子2でも言えるので,両方のスピンの合成状態の演算子;
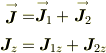
について,各粒子の角運動量の固有状態と同様に;
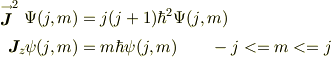
となる.ただし,合成された波動関数合は,次の様に展開される;
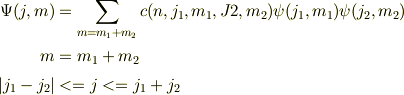
#ここで,「n」は例えば,動径方向の量子数.
と考えて良いのだろうと思います.
今回の場合で言えば,
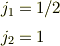
ですね.
肝心な点を書き忘れていたので追加します.古典力学でも角運動量はヴェクトルです.質点で言えば;
角運動量演算子の合成を考えます;
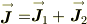
粒子1,2の座標については,微分演算があっても,変数としては独立ですから,演算子としての粒子サフィックスは交換出来るので,通常のヴェクトルの内積計算で良いので,辺々を自乗して,
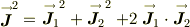
この演算子を波動関数 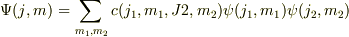 に作用させたとかんがえて,
に作用させたとかんがえて,
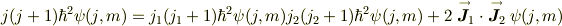
となるので,形式的に
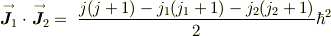
と書く事が多いのだと思います.しばしば, 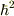 を落として論議する事もありますね.
を落として論議する事もありますね.
なお,内積は個々の成分の射影成分 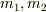 には異存しないのは,古典力学のヴェクトル間の内積の性質と合致します.
には異存しないのは,古典力学のヴェクトル間の内積の性質と合致します.
Re: スピンの合成
hibikaisou さんのレス (2009/06/28(Sun) 22:59)
ありがとうございます.
馬鹿な質問かも知れませんが,
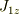 と
と 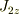 について
について 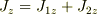 って2×2と3×3の行列の足し算なので計算できないと思ったんですが計算できるのですか?
って2×2と3×3の行列の足し算なので計算できないと思ったんですが計算できるのですか?
Re: スピンの合成
mNeji さんのレス (2009/06/28(Sun) 23:16)
> 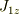 と
と 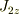 について
について 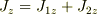 って2×2と3×3の行列の足し算なので計算できないと思ったんですが計算できるのですか?
って2×2と3×3の行列の足し算なので計算できないと思ったんですが計算できるのですか?
私は,角運動量の行列表示での考え方を知らないので....おそらく,演算子の行列成分が直接観測量になるのではなく,演算子の固有状態を表す「固有値」と「固有関数」とのセットで物理量を規定出来るからだと思います.
もし,「表現行列が違う」のが本質的ならば,原子での「電子のスピン 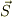 」と「電子の軌道運動量
」と「電子の軌道運動量 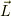 」との和も考えられなくなってしまいますね.
」との和も考えられなくなってしまいますね.
ここら辺の原理的な考え方をご存知の方の助言をお願いします.
Re: スピンの合成
HY さんのレス (2009/06/29(Mon) 00:25)
sa=1/2,sb=1なのでs=1/2,3/2の2つだから
Sa・Sbの固有値は 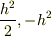 ですね.
Szの固有値が
ですね.
Szの固有値が 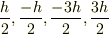 ですね.
ですね.
Re: スピンの合成
hibikaisou さんのレス (2009/06/29(Mon) 08:01)
ありがとうございました.固有状態については分かりますか???
Re: スピンの合成
mNeji さんのレス (2009/06/29(Mon) 08:21)
実際の値については,ご自分で計算する事をお勧めします.
注意するべき点は,
・内積の値は,必ずしも変化幅が1では無いこと.その係数はあくまで 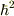 であること.
・射影の値は,個々の成分の最小〜最大値の単純加算で,変化幅が1であること.その係数はあくまで
であること.
・射影の値は,個々の成分の最小〜最大値の単純加算で,変化幅が1であること.その係数はあくまで 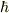 であること.
であること.
Re: スピンの合成
hibikaisou さんのレス (2009/06/29(Mon) 15:27)
ありがとうございます. 計算は自分でやってみます.ですが計算方法が分からないので, 固有状態の計算の手順だけでも教えてもらえませんか??
Re: スピンの合成
mNeji さんのレス (2009/06/29(Mon) 15:56)
>固有状態の計算の手順だけでも教えてもらえませんか??
必要な式は全て書いたつもりなのですが....
「固有状態」とは,固有関数を意味しますか?もすこし具体的にお知りにないたい点を書いてくだされば,検討してみます.
Re: スピンの合成
mNeji さんのレス (2009/06/29(Mon) 17:23)
始めのご質問の
>次に固有状態ですが,Sa・Sbの固有状態は 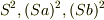 の固有状態と同じものですか?
の固有状態と同じものですか?
という意味でしょうか?それならそうだと考えて良いと思います.いま,近くの図書館から量子力学の教科書を借りて来ました;
物理学ライブラリー 8 量子力学 II 朝倉書店 高田 健次郎・著 1983-04
です.このp137からに,「付録角運動量の合成」という部分に「角運動量の合成則」という説明があります.それに沿って,角運動に関する波動関数の合成を端折って引用します;
粒子1の波動関数が 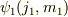 ,粒子2の波動関数が
,粒子2の波動関数が 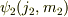 があるときの適当な線形結合によって,角運動量が合成
された波動関数,
があるときの適当な線形結合によって,角運動量が合成
された波動関数, 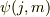 できる,
できる,
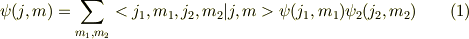
なお, 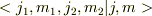 をクレブッシュ-ゴルダン係数(Clebsch-Gordan Coefficients)という.
をクレブッシュ-ゴルダン係数(Clebsch-Gordan Coefficients)という.
ここで, 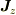 について,
について,
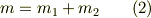
またベクトルの合成に関する三角条件より,
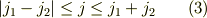
簡単な場合のクレブッシュ-ゴルダン係数
表1 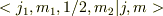
Re: スピンの合成
mNeji さんのレス (2009/07/01(Wed) 06:00)
もうご覧になっていないかもしれませんが,スピンの固有関数の丁寧な説明として, http://w ww.mns.kyutech.ac.jp/~okamoto/education/quantum/spin-coupling060614b.pdfがありました.ご参考まで.