もんちょ さんの書込 (2009/06/26(Fri) 11:48)

はじめまして，もんちょというものです．

重心の考え方で質問があります．

複数の3Dモデルからなる一つの3Dモデルの重心を求めるとき， それぞれの板厚，密度を用いて算出する事ができるかと思います．

そこで複数のモデル同士が接合されているという条件で， 接合の仕方で重心は変化するのでしょうか？

例→重なっている部分を一点接合する →重なっている部分を全て接合する

表現の仕方がいまいちかと思いますが，ご回答頂ければ幸いです．

mNeji さんのレス (2009/06/26(Fri) 13:30)

もんちょ初めまして．

えーと，アニメーションなどで，大きなロボットの部分(頭部，胴体，腕，脚)などが，別々に飛んで来て合体するようなイメージでしょうか．

「重なっている部分を一点接合する」のが簡単ですから，それで考えます．

仮に，４つの部分からなるとして，それぞれの質量と重心位置は前もって，判っているとします．

<pre> 部品＃質量 座標 質量＊座標 1 M1 (X1,Y1,Z1)M1*(X1,Y1,Z1) = (M1*X1,M1*Y1,M1*Z1) 2 M2 (X2,Y2,Z1)M2*(X2,Y2,Z2) = (M2*X2,M2*Y2,M2*Z2) 3 M3 (X3,Y3,Z3)M3*(X3,Y3,Z3) = (M3*X3,M3*Y3,M3*Z3) 4 M4 (X4,Y4,Z4)M4*(X4,Y4,Z4) = (M4*X4,M4*Y4,M4*Z4) ----- -------------------- 質量の合計 質量＊座標の合計

とすれば，重心の質量MGは「MG=質量の合計」で，重心の座標を(XG,YG,ZG)とすると，

質量＊座標の合計 (XG,YG,ZG) = ーーーーーーーーー 質量の合計

(M1*X1,M1*Y1,M1*Z1) + (M2*X2,M2*Y2,M2*Z2) + (M3*X3,M3*Y3,M3*Z3) + (M4*X4,M4*Y4,M4*Z4)

=ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

M1 + M2 + M3 + M4

(M1*X1+M2*X2+M3*X3+M4*X4, M1*Y1+M2*Y2+M3*Y3+M4*Y4, M1*Z1+M2*Z2+M3*Z3+M4*Z4)

=ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー M1 + M2 + M3 + M4 </pre>

すなわち，それぞれの部品の重心に，それぞれの質量が集まった質点からなる系の重心を考えれば良い事になります．

toorisugari no Hiro さんのレス (2009/06/26(Fri) 13:40)

これって，共に合同な形をしているが，片方にはひびはなく，もう片方にはひびがはいっている(欠損はない)，二つの物体の重心は一致するか?という問題と同じですよね．

重心は一致します．

重心の計算式

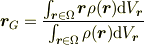
と， 密度 が有限なら，体積が変わらないように領域 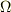に切れ目を入れても，積分値に変化はないこと， をあわせて考えると重心は一致することが導けますね．

もんちょ さんのレス (2009/06/26(Fri) 17:12)

＞mNejiさん ＞toorisugari no Hiroさん

回答有難うございます！

重心の計算式から力(重力)などの外力は含まれないので，複数のモデルの合計の重心は計算式で求められるので理解できます．

ですが，実物でのイメージでは，ボルト結合やスポット結合などを用いて複数の物体を異なる結合方法で結合すると，釣り合いの取れる位置に重心が移動する気がすします・・・

それは重心ではなく，力点(？)のような考え方になるのでしょうか？ それとも実際の物体になると静的ではなく動的な考え方になり，重力による変形と時間によって，重心が変化するために，自分の持っているようなイメージになるでしょうか？

transfer さんのレス (2009/06/26(Fri) 17:57)

もんちょさんのそのイメージでほぼ合っていると思います．（釣り合いの取れる位置に重心が移動する気がする） 厳密には重心ではなく，質量中心という言い方が正しいですね．

ところで，ここが気になったのですが， 個々の３Dモデルのパーツの固有の座標系（パーツ座標系と呼ぶ）での質量中心とそこに集中している質量の値がわかっているわけですよね． それで問題は，それらの複数のパーツを１つの大きな座標系の中に配置したときに，全体としての質量中心がどこにあるか？という問題ですよね？ だとしたら，１つの大きな座標系（全体座標系と呼ぶ）に複数のパーツを配置してまとめるときに，個々のパーツ座標系との間で座標変換が必要になります． （一般に，全体座標系と個々のパーツ座標系との間では，座標原点も異なりますし，座標軸の方向とかも異なりますから）

以上の全体座標系と個々のパーツ座標系との間の座標変換の問題がクリアされていれば（つまり，全体座標系における個々のパーツの質量中心座標がわかれば）， パーツを組み合わせた全体の質量中心座標 ＝（Σ各パーツの質量 × 全体座標系における各パーツの質量中心座標）/（Σ各パーツの質量） となります． 要は，全体座標系において，個々のパーツの質量中心の座標が正しく求められるかどうかだと思います．（シミュレーション等をする場合）

もしも最初の質問にある「一点接合」と「全て接合」の違いによって，全体座標系における個々のパーツの質量中心座標が変わるというのであれば，全体としての質量中心は変わってきます． こういうことですよね？

mNeji さんのレス (2009/06/26(Fri) 22:53)

＞それは重心ではなく，力点(？)のような考え方になるのでしょうか？ ＞それとも実際の物体になると静的ではなく動的な考え方になり，重力による変形と時間によって，重心が変化するために，自分の持っているようなイメージになるでしょうか？

これは接合した部品が静止しているのではなくて，合体したロボットの運動を考えるということでしょうか？

何れにしろ，どのような状況を考えるかを規定しないと，問題が判らない様にかんじますね．

transfer さんのレス (2009/06/27(Sat) 09:24)

前提条件として，１つの座標系の中で，各パーツの質量の値とそのパーツの重心座標（つまり各パーツの重心の位置ベクトル）は，すべてわかるものとします． また，「一点接合する」とか「全て接合する」という操作においては，新たな質量の増加はなしとします．

それで，

> そこで複数のモデル同士が接合されているという条件で，
> 接合の仕方で重心は変化するのでしょうか？

というのが最初の質問ですから， 動いていない静的な状態に，単にある形にパーツを組み上げたとき，

1. 接合の仕方でパーツの位置が変わらないとき＝＝＝＞全体の重心は変わらない
2. 接合の仕方でパーツの位置が変わるとき＝＝＝＞全体の重心は変わる

となります． 例えば簡単のために一次元の(A)と(B)という２つのパーツからなる物体を考えます． (A)と(B)の接合箇所は１箇所のみで，しかも，(A)と(B)はまっすぐにしか接合できないとします． そのとき， 接合の仕方で(A)+(B)の全体の長さが変わらないのであれば，全体の重心は変わりませんし， 接合の仕方で(A)+(B)の全体の長さが変わるのであれば，全体の重心は変わります．

接合の仕方がどうこうという細かい話を抜きにすれば， 動いていようが（動的）静止していようが(静的），全体の重心は先に示したように， 全体の重心の位置ベクトル ＝ （Σ各パーツの質量 × 各パーツの重心の位置ベクトル）/（Σ各パーツの質量） で与えられます． Σ の代わりに∫ で書いても同じです． 一般的に，物体が動いている状況を考えれば，位置ベクトルは時間の関数ですから，当然，全体の重心の位置ベクトルも時間の関数となり，時間的に変化してもかまいません．

この問題から離れて一般的に言って，１つの座標系において， 人が姿勢を変えるだけ（腕を水平にまっすぐ前に突き出す・片足を上げる・しゃがむなど）で，その人の重心の位置は可能な範囲でいくらでも変わります． まさにもんちょさんがイメージされた通り，動的に重心が移動します． 人が歩くということ自体，重心をわざと変化させる動作です．

物体が形を変形させるだけで重心が変わるというのは，一様な１本の太いロープを考えてもわかります． ロープがまっすぐにのびていれば，ロープの重心はロープの長さのど真ん中にありますが， ロープが丸く輪を作れば，そのときのロープの重心は，輪である円の中心にあり，もはやロープの上にはありません．

また，いろんなパーツを組み上げて１つの物体にしていく途中においても，その過程における一塊の重心は時間的にいくらでも変化してかまいません． これは積み木を組み上げるときのことを考えれば明らかです． 積み上げ方によって途中で崩れるか崩れないかの違いが出てくるのは，まさに重心が移動するからです．

もんちょ さんのレス (2009/06/29(Mon) 12:05)

みなさん回答有難うございます！

＞mNejiさん 表現の仕方がいまいちで申し訳ありません... しかし，必要以上に詳しく記載すると機密事項に関わってきますので控えさせて下さい． なお，ロボットではありませんｗ

＞transferさん 的確な回答有難うございます！！ やっと１つの謎が解けました(笑) 静的な状態において質量の変化がなかったら重心の変化もないということだったんですね... 搬送時に起こる重心のずれは，やむなしと言ったところでしょうか↓↓

transfer さんのレス (2009/06/29(Mon) 22:05)

> 静的な状態において質量の変化がなかったら重心の変化もないということだったんですね

その通りです． しかし，重心というのは，あまり難しく考えるものでもないと思いますけどね． とにかく，ある瞬間の重心の定義は３人とも共通に示した通りですから，それで計算すればいいだけです． （厳密には重心と質量中心は異なりますが，多くの場合，両者は同一と見なしてかまいません．ここで示したのは，質量中心の定義です） また，動的な場合でも，条件がそろえば，常に重心を一定に保ったまま変形することもできます． （簡単な例だと，一様な密度の物体が，球対称に広がったり収縮したりする場合など）

> 搬送時に起こる重心のずれは，やむなしと言ったところでしょうか

車両の転倒ばかりでなく，船も許容範囲を超えて大幅に重心が移動すると転覆します． 重心が変化するのは避けられないので，それを見越して物は設計されてはいますが，限度を超えると事故につながります．