電磁場中の荷電粒子の・・・

ヒノッキーさんの書込 (2009/06/26(Fri) 00:14)

どうも，ヒノッキーです．・・・助けてください．（笑）

電磁場中の荷電粒子のシュレーディンガー方程式を利用する問題を解いているのですが，vとpの期待値を求めた際，Ａをベクトルポテンシャル，eを電荷，ｐを運動量とすると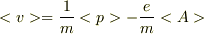， $<v> =\frac{1}{m}<p>-\frac{e}{m}<A>$ ・・・と，なりました．ここでなぜ，vを求める際に，Aがかかってくるのかわかりません・・・．

ｐ＝ｍｖの関係が成り立たないのはなぜなのでしょうか？それと，ｖがゲージ不変なのに，ｐはゲージ不変にはならないことも，なぜなのかわかりません．

ｍが一定でなく，ベクトルポテンシャルに依存して変化する？などと考えていて，混乱しています．

お願いします．どなたか，アドバイスをいただけませんか？

（もし，この内容が挙げられている図書などがありましたら，教えてください．）

Re: 電磁場中の荷電粒子の・・・

ヒノッキーさんのレス (2009/06/26(Fri) 00:33)

二つの質問をしたのですが，質問内容を変えさせてもらいます．

ｐがゲージ不変でないため，ｖをゲージ不変にするためには，Ａを付け加える必要があると考えれば，ｐ＝ｍｖの不思議は解決できました．

質問を，「なぜｐがゲージ不変ではないのか」にしぼります．

ｖとｐの違いはいったい何なのでしょうか？

Re: 電磁場中の荷電粒子の・・・

mNeji さんのレス (2009/06/26(Fri) 00:39)

私は，このレベルには到達していないのて，検索係を拝命してみました；yahooで「電磁場中の荷電粒子シュレーディンガー方程式」としてみたら，

（１）パウリ方程式(PDF) http://members3.jcom.home.ne.jp/nososnd/ryosi/pauli.pdf があっさりと解説されているようです．

（２）基礎量子力学猪木慶治川合光講談社 http://shop.kodansha.jp/bc2_bc/search_view.jsp?b=1532405 この本はは意見した事が無いのですが，目次では一章がさかれています．おっと，「1次元の問題―束縛状態」もある(笑)！

〜〜〜〜勿論，他の識者の方々のご推薦を優先下さい．ご参考まで．

Re: 電磁場中の荷電粒子の・・・

mNeji さんのレス (2009/06/26(Fri) 01:37)

＞ｐがゲージ不変でないため，ｖをゲージ不変にするためには，＞Ａを付け加える必要があると考えれば，ｐ＝ｍｖの不思議は解決できました．

先に書いた参考資料(1)を拝見していると，・p = mv + eA ですが，

左辺pは「系全体の運動量」であり，これが『「粒子の運動量」と「電磁場の運動量」との和である』と読めないでしょうか？だから，

粒子の運動量(mv) = 系全体の運動量(p) -電磁場の運動量(eA)

〜〜〜〜どのみち，ディラックさんのQMをお読みになった方々様，宜しくお願いします．

Re: 電磁場中の荷電粒子の・・・

ヒノッキーさんのレス (2009/06/26(Fri) 02:37)

mNejiさん，ありがとうございます．

＞左辺pは「系全体の運動量」であり，これが『「粒子の運動量」と「電磁場の運動量」との和である』と読めないでしょうか？

「電磁場の運動量」ですか・・・．なるほど，確かにそう考えればうまくいきますね．考えつきませんでした．

ｖは，「粒子の運動量」であり，「電磁場の運動量」が入ってはいけないので eAだけを除く必要がある，と考えれば最初のｖの式にも納得です．

ｐがゲージ不変でないのも，「電磁場の運動量」に任意性が残るから，と考えられ，疑問も解消です．

・・・でもそれだと，どうも納得できない部分があるんです．それでは，最初の式の最後の項を「電磁場の速さ」のようなものと定義できて，これは，ゲージ不変でない・・・．

・・・つまり，「電磁場の速さ」なるものは，如何様にもとれるということになってしまいます．これは物理的に意味のない項だから考えないのでしょうか？それとも，エネルギーの遅延ポテンシャルとなにか関係があるのでしょうか？

・・・すみません，質問の内容が増えてしまいました．

Re: 電磁場中の荷電粒子の・・・

mNeji さんのレス (2009/06/26(Fri) 09:21)

＞それでは，最初の式の最後の項を＞「電磁場の速さ」のようなものと定義できて，＞これは，ゲージ不変でない・・・．

系全体のゲージ不変性はあるのでしょうね．でも，それなら粒子もすくなくとも特殊相対性理論の枠組みで論議されているのですか？

＞・・・つまり，「電磁場の速さ」なるものは，＞如何様にもとれるということになってしまいます．

少なくとも「電磁場の位相速度は光速」ですよね？

〜〜〜〜私も，学生の頃，この手の領域に興味を持っていたのですが，数学が得意でなかったのと，ノートを書いても字が汚かったので自ら判読出来ないという二重苦しみのために，手がつけられませんでした．

ぜひとも，この数学掲示版を活用されて論議をされて戴ければ，私も門前の小僧で...．

Re: 電磁場中の荷電粒子の・・・

toorisugari no Hiro さんのレス (2009/06/26(Fri) 10:00)

この問題って，量子力学だけでなく，電磁気学や解析力学の深い理解が求められるもので，正直，分かってないです．ですから，以下に述べることにも間違いがあると思うので識者よろしく．

> Ａをベクトルポテンシャル，eを電荷，ｐを運動量とすると，
>  |598fca482e59c771686e18869a95e8f8| 
> ・・・と，なりました．
> ここでなぜ，vを求める際に，Aがかかってくるのかわかりません・・・．

これの答えは「世界がそうなっているから」しかないと思います．

もちろん「方程式に含まれる正準運動量に 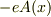-eA(x) を付け加えておけば，波動関数を 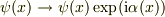$\psi(x)\to\psi(x)\exp(\mathrm{i}\alpha(x))$ と変換しても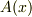， A(x) のゲージ変換に繰り込むことで方程式を不変に保てる」というDiracなどの発見や相対論的な変分原理を学ぶと，「自然」だと思えるものではあるのですが．

そもそも，電磁場がからむ解析力学の概念を「ニュートン力学」の範囲で理解したいって，無理がありませんか?

> ｐ＝ｍｖの関係が成り立たないのはなぜなのでしょうか？

そもそも正準運動量は「運動量」と違うものですし，後者でさえ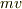であるのはニュートン力学の範囲内です．

>> 『「粒子の運動量」と「電磁場の運動量」との和である』

「電磁場の運動量」は別に存在するので，この表現はまずいと思います．

> それと，ｖがゲージ不変なのに，ｐはゲージ不変にはならないことも，なぜなのかわかりません．

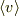$\langle v \rangle$ はユークリッド幾何学的に測定可能な量ですので，「ゲージが測定可能でないのなら」（＝電磁気学の体系がゲージ不変なら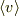）， $\langle v \rangle$ はゲージの取り方に影響受けるはずはありません．(影響を受けたらゲージが測定可能になってしまいます．)

> 質問を，「なぜｐがゲージ不変ではないのか」にしぼります．

正準運動量が何なのか理解していないので，わかりません．

Re: 電磁場中の荷電粒子の・・・

ヒノッキーさんのレス (2009/06/26(Fri) 16:50)

mNejiさん，＞少なくとも「電磁場の位相速度は光速」ですよね？

僕もそうだと認識しています．

toorisugari no Hiroさん，返信ありがとうございます．今日，先輩にいろいろ聞いてみたのですが，言われているとおり，正準運動量と一般運動量の取り違えによる勘違いが原因でした．

しかし，僕も正準運動量がなんなのか，よく分かっていません．これから勉強して，もしわかったら自分でも挙げていきます．

とりあえず今の疑問は，「正準運動量とはなんなのか」です．これが解消されれば，すべての疑問が解ける気がします．

もし，詳しい方がいらっしゃったらアドバイスをいただけませんか．

Ｐ.Ｓ.mNejiさん

＞ノートを書いても字が汚かったので自ら判読出来ないという・・・

僕も同じです・・・．キレイに書くのって難しいですよね（笑）

[home] [掲示板] [ページの先頭]