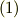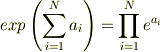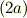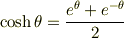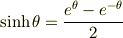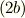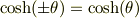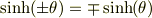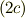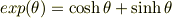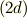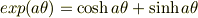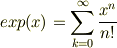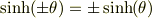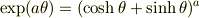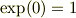円卓モデルにおける対称性と相関関数について
円卓モデルにおける対称性と相関関数について
mittwoch さんの書込 (2009/06/24(Wed) 17:35)
初めまして.大学1年生です. 講義の中でどうしても理解できない問題がありましたので, 質問させていただきます.
1列に並んだスピンに関して,各スピンに,1,2,・・・Nと番号をつける. このとき,Nと1は隣り合っている. 各スピンは2つの状態±1をとり,これを状態変数σx = ±1と表す. このとき一意的な定常分布を
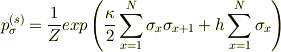
と表す. このとき,
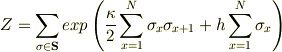
は規格化因子である. さて,
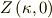
を計算し,
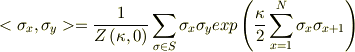
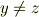
を求めよ.
という問題です. 講義においては,分配関数の確率幾何的表現というもので 式を展開し計算しているのですが,結果的にどのような解が得られるのか さっぱり分かりません. 実際,h=0で計算するとZが0になってしまい計算できません. 調べるにも何を調べてよいか分からず困っています. 根本的なところから解説してくださる方,お願いします.
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/24(Wed) 19:56)
> 実際,h=0で計算するとZが0になってしまい計算できません.
何故?
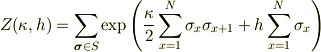
指数関数の中身が有限な実数なら,指数関数は正であり,指数関数の総和が0になることはないですが.
Re: 円卓モデルにおける対称性と相関関数について
トラ さんのレス (2009/06/24(Wed) 20:43)
1列に並んだスピンに関して,各スピンに,1,2,・・・Nと番号をつける. このとき,Nと1は隣り合っている.
Re: 円卓モデルにおける対称性と相関関数について
mittwoch さんのレス (2009/06/25(Thu) 00:00)
ご指摘の通り0になるはずありませんよね. 分配関数の確率幾何的表現による展開が理解できていないためだと思われるので, ほかの解き方はないでしょうか?
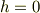
ですので,結果的に一番に求めたいのは,
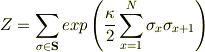
なのですが,どのような考え方を用いてよいのか分かりません. 変数σをどのように扱えばよいのでしょうか?
Re: 円卓モデルにおける対称性と相関関数について
サメ さんのレス (2009/06/25(Thu) 01:04)
分配関数の確率幾何的表現による展開が理解できていない
結果的に一番に求めたいのは,規格化因子
変数σをどのように扱えばよいのでしょうか?
Re: 円卓モデルにおける対称性と相関関数について
mNeji さんのレス (2009/06/25(Thu) 09:25)
mittwochさん,横から失礼します.
素人の感触ですが,スピン1/2を持つ,例えば電子が数珠繋ぎのように配置していて,其れに外部磁場が印可されている様な場合の確率密度をだそうとしているのではないでしょうか.
「h」の項は,磁束密度とスピンとの内積.「κ」の項は,2つのスピン間の相互作用では.
「h=0」というのは,外部磁場が切られているばあいで,そのとき,系がスピン・スピン相互作用のもとに,熱平衡にある状態に対応する,ようなイメージでしょうか.
はなはだ定性的な論議しか出来なくて恐縮です.
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/25(Thu) 10:39)
> どのような考え方を用いてよいのか分かりません.変数σをどのように扱えばよいのでしょうか?
Ising modelの分配関数の計算の仕方は統計力学の本に載ってる話ですが,
> 分配関数の確率幾何的表現による展開が理解できていないためだと思われる
まず,こちらを先に理解すべきでは?
どのような説明だったかを再現してください.
Re: 円卓モデルにおける対称性と相関関数について
ライオン さんのレス (2009/06/25(Thu) 11:11)
グタイテキナカズデコレモサイゲンシテホシイ
1列に並んだスピンに関して,各スピンに,1,2,・・・Nと番号をつける. このとき,Nと1は隣り合っている. 各スピンは2つの状態±1をとり,これを状態変数σx = ±1と表す.
実際,h=0で計算するとZが0になってしまい計算できません.
Re: 円卓モデルにおける対称性と相関関数について
mittwoch さんのレス (2009/06/25(Thu) 14:13)
たくさんの返信ありがとうございます. >mNejiさん 具体的な例を挙げればその通りだと思います. 問題は,その一般的な例について解くものだと思います. >toorisugari no Hiroさん 統計力学の本に載っているんですね.しかし,この講義は統計力学ではないため, できる限りに本講義にそった形で解答したいと思っています. できる限り,正確に講義における説明をのせたいと思います.
結局
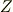
は以下のように書き直すことができる.
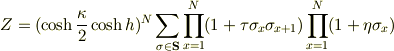
ただし,

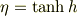
ここで,
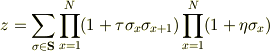
とおいて,この

を計算したい. 展開した上で,各項について
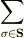
をとると,結果的には,
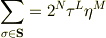
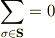
に場合分けできる. ただし,上の式は,
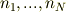
がすべて偶数の場合であり,下の式はそれ以外の場合である. (ただし,nはσ各を何乗しているのかを表している.) 結局,
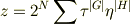
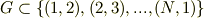
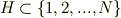
ただし,
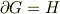
と,このような方法で展開しています. しかし,結局これが何を表しているのか分かりませんし, 具体的な計算方法に至っては皆目分かりません. (そもそもこれが具体的な計算の結果なのか,そうでないのかも分かりません.) 必要な情報が抜けているかも分かりませんが,よろしくお願いします.
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/25(Thu) 14:32)
ちょっと,時間がないのでfollowを今できませんが, とりあえず. TeXの表記にcoshとsinhとtanhを使ってください.立体になるので見やすくなります.また,SigmaとPiでなくsumとprodを使ってください.
また 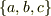 のように書きたければ{a,b,c}でなく{a,b,c}としてください.
のように書きたければ{a,b,c}でなく{a,b,c}としてください.
Re: 円卓モデルにおける対称性と相関関数について
mNeji さんのレス (2009/06/25(Thu) 18:28)
具体的なイメージが判らないので,系が仮に独立なN個の電子で,空間的には区別できるとします.電子系の全スピンをSとし,N=1から始まって,Sがどのように変わるかを考えて見ますと;
<pre> (スピン配置) N S 1 1/2 (+); (-) 2 0 1 (+,-)-(-,+); (-,-) (+,-)+(-,+)(+_,+) 3 1/2 3/2 以下略 4 0 1 2 </pre>
見たいな感じになって,同一のSでラベルを貼っても,スピン配置は複数の組み合わせが出て来ませんか?
と,書いて見ましたが,やはり変ですかね.
Re: 円卓モデルにおける対称性と相関関数について
ワシ さんのレス (2009/06/25(Thu) 18:49)
講義においては,分配関数の確率幾何的表現というもので 式を展開し計算しているのですが,結果的にどのような解が得られるのか さっぱり分かりません.
しかし,結局これが何を表しているのか分かりませんし, 具体的な計算方法に至っては皆目分かりません. (そもそもこれが具体的な計算の結果なのか,そうでないのかも分かりません.) 必要な情報が抜けているかも分かりませんが,よろしくお願いします.
ドノヨウニシテ
h=0で計算するとZが0になってしまい計算できません.
トケツロンシタノカ?
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 イツマデニカイトウガホシイノカ? ホカノニンゲンハコウギヲリカイシテイルノカ?
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/25(Thu) 20:27)
> 電子系の全スピンをSとし
全スピン(=スピンの和)とSは違うものでしょ.SはN個のスピン集団の取りうるパターンの集合 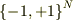 です.もちろんSの定義によりますが,すくなくとも,
です.もちろんSの定義によりますが,すくなくとも,
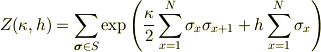
における 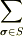 とは
とは
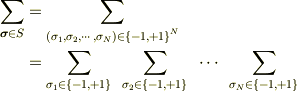
のことですよ.
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/25(Thu) 20:42)
とりあえず問題.
「
(1) 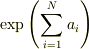 の指数関数の中の総和を指数関数の外に出せ.
の指数関数の中の総和を指数関数の外に出せ.
(2a) 双曲関数 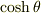 ,
, 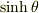 を指数関数で定義せよ.
(2b)
を指数関数で定義せよ.
(2b) 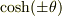 ,
, 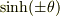 の
の 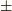 を関数の外に出せ.
(2c)
を関数の外に出せ.
(2c) 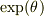 を
を 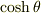 ,
, 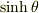 で表せ.
(2d)
で表せ.
(2d) 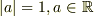 として
として 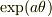 を
を 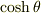 ,
, 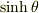 ,
,  で表せ.
」
まずはこんなところかな.
これを解いてくれないと先に進めませんね.
で表せ.
」
まずはこんなところかな.
これを解いてくれないと先に進めませんね.
Re: 円卓モデルにおける対称性と相関関数について
mNeji さんのレス (2009/06/25(Thu) 21:37)
>全スピン(=スピンの和)とSは違うものでしょ.
そうですね,少なくともある軸(仮にz軸とする)にそった(射影)成分 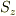 ,がでます.従って,全スピン角運動量固有値Sは,
,がでます.従って,全スピン角運動量固有値Sは,
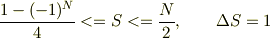
ですよね.ただ,このモデルにとって「全スピンが意味を持つかどうか」は別問題ですね.
う〜む.では,すこし観点を変えますと,ある「パターンの集合の一つ」で, 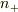 個が
個が 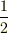 の射影をもち,
の射影をもち, 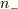 個が
個が 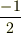 だとすれば,
だとすれば, 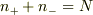 で,
で,
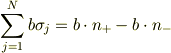
になりますね....
Re: 円卓モデルにおける対称性と相関関数について
mittwoch さんのレス (2009/06/27(Sat) 02:39)
すみません.大分混乱してきました. そもそも,この関数は計算できるのでしょうか? 変数を置き換えただけで,結局具体的な展開がなされていないように 思えるのですが・・・.
Re: 円卓モデルにおける対称性と相関関数について
トド さんのレス (2009/06/27(Sat) 03:20)
ダサレタモンダイハトイタノカ?
イツマデニカイトウガホシイノカ?
統計力学の本に載っているんですね.しかし,この講義は統計力学ではないため, できる限りに本講義にそった形で解答したいと思っています.
トイウノデアレバ分配関数の確率幾何的表現による展開ヲリカイスベキデアロウ
ホカノニンゲンハコウギヲリカイシテイルノカ?
Re: 円卓モデルにおける対称性と相関関数について
ヒヒ さんのレス (2009/06/27(Sat) 03:57)
そもそも,この関数は計算できるのでしょうか?
ドノヨウニシテ
h=0で計算するとZが0になってしまい計算できません.
トケツロンシタノカ?
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/27(Sat) 08:38)
> 具体的な展開がなされていないように思えるのですが・・・.
結果を整理した以下の式はぎりぎりの変形ですよ.(  についての計算は終わっているので,答と言っても良いですね.)
についての計算は終わっているので,答と言っても良いですね.)
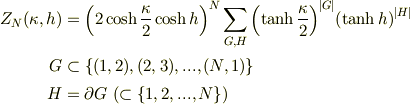
# 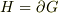 にちょっと感動しました.このあたりが「幾何学」ですね.
にちょっと感動しました.このあたりが「幾何学」ですね.
> この関数は計算できるのでしょうか?
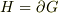 の意味さえ分かっていれば,
の意味さえ分かっていれば, 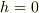 の場合は直ぐに「簡単な式」にできます.
#
の場合は直ぐに「簡単な式」にできます.
# 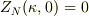 じゃないですよ.念のため.
じゃないですよ.念のため.
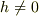 の場合,これ以上簡単な式が存在するのか私は知りません.双曲関数の多項式の形になりますが,その係数(0または自然数)は,たとえば計算機で簡単に計算できます.
# 変形前の式だとかなりの計算資源が必要で,それでも,いくつかの
の場合,これ以上簡単な式が存在するのか私は知りません.双曲関数の多項式の形になりますが,その係数(0または自然数)は,たとえば計算機で簡単に計算できます.
# 変形前の式だとかなりの計算資源が必要で,それでも,いくつかの 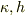 の組に対する
の組に対する 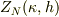 の数値解を得るのがやっとでしょう.
の数値解を得るのがやっとでしょう.
Re: 円卓モデルにおける対称性と相関関数について
mittwoch さんのレス (2009/06/28(Sun) 00:31)
>toorisugari no Hiroさん なるほど.この式がかなり展開された形と考えてよいわけですね. しかし,ここが一番の疑問なのですが, ここに
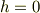
を代入した場合,どうなるのでしょうか?
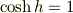
ですので,括弧内は良いとして,
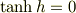
ですよね? (ここが間違っているとは思うのですが・・・.) ここからどうすればよいのか分かりません. 分からない事だらけで申し訳ありませんが,お願いします.
Re: 円卓モデルにおける対称性と相関関数について
ホオジロザメ さんのレス (2009/06/28(Sun) 02:55)
ここからどうすればよいのか分かりません. 分からない事だらけで申し訳ありませんが,お願いします.
アクビガデテキタ
エンエンオワリノミエナイゲームヲツヅケルモヨシオワラセルモヨシ
ツギモ
分からない事だらけで申し訳ありませんが,お願いします.
ノクリカエシダナ
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/28(Sun) 11:37)
> 括弧内は良いとして, 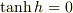 ですよね?
> ここからどうすればよいのか分かりません.
ですよね?
> ここからどうすればよいのか分かりません.
ここで安直に 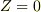 としてしまったのでしょう?間違いです.
これは,高校レベルの概念を理解していないことになるので,自分で考えてください.
としてしまったのでしょう?間違いです.
これは,高校レベルの概念を理解していないことになるので,自分で考えてください.
ヒントの問題: 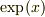 のテーラー展開を総和
のテーラー展開を総和 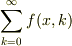 の形で書いてください.「その総和を用いて」
の形で書いてください.「その総和を用いて」 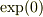 を計算してください.
を計算してください.
先に進みたいのは分かりますが,私の問題(前に出したものを含めて)に答えてくれないと,これ以上の説明はできません.
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/29(Mon) 09:23)
(2b)(2d)以外はあっています.
(2b)は丁寧に場合分けして計算してください.
また,(2d) 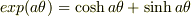 では,詰めが甘いです(問題の条件に合致していません).
では,詰めが甘いです(問題の条件に合致していません).
# 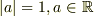 を使ってませんね.
# ヒントは既に与えてあるので,注意深く問題を見直してください.
# TeX: expじゃなくexpの方がよいです.
を使ってませんね.
# ヒントは既に与えてあるので,注意深く問題を見直してください.
# TeX: expじゃなくexpの方がよいです.
>> ヒントの問題: 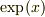 のテーラー展開を総和
のテーラー展開を総和 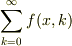 の形で書いてください.「その総和を用いて」
の形で書いてください.「その総和を用いて」 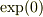 を計算してください.
を計算してください.
> |1334a118b0b55bc29c852bf2e7a5a7a7|
添え字が間違っています.で,『「その総和を用いて」 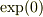 を計算』は?
を計算』は?
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/29(Mon) 14:04)
> (2d) 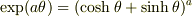
ああ,これでも問題の条件に合致していますが,今回はこれではないです.
相変わらず 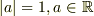 を利用していないですね.(2b)と組み合わせてください.
を利用していないですね.(2b)と組み合わせてください.
> |ddfd224602cf47d2fa0108e5bb1d6fc1|
相変わらず間違い(これじゃ 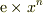 ).あとinfty
).あとinfty
> |4102706eeeb431ba9163c774cb1378b5| > (最初の項を除いてすべてxについての多項式であるので)
前半はもちろん正解ですが,後半は?. 何故最初の項を除くのでしょうか?最初の項も含めて「xについての多項式」ですよ.
Re: 円卓モデルにおける対称性と相関関数について
mNeji さんのレス (2009/06/29(Mon) 15:53)
toorisugari no Hiroさん,横から失礼します.数学の処方に付いては興味深く拝見しています.
ところで, 指数関数のテーラー展開は,今回の計算に必須でしょうか?
仮にηに関わる積の項で(1+ησj)を展開してηのベキ状で纏めて,そこだけに注目して総和をとってみると,対称性からすべて落ちてしまう様に見えます.
恐らく,τにかかわる積のτのベキと合わせて,総和を取った時に,符号がのこる成分があるような...,気がしますが.ここら辺でテーラー展開を使うのですかね?
#門前の小僧で見ているのですが,目の前に数式がちらついてしまって(汗).
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/29(Mon) 16:14)
> 指数関数のテーラー展開は,今回の計算に必須でしょうか?
直接必要ないです. 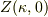 の計算でヒントの問題と同じ考え方が必要というだけです.
の計算でヒントの問題と同じ考え方が必要というだけです.
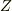 の展開は(1)(2d)ができれば,第一段階クリアです.No.24333の考えを2度使い変形して,
の展開は(1)(2d)ができれば,第一段階クリアです.No.24333の考えを2度使い変形して,  で和を取り,出てきた拘束条件を幾何学的に解釈すれば終了です.
で和を取り,出てきた拘束条件を幾何学的に解釈すれば終了です.
Re: 円卓モデルにおける対称性と相関関数について
mNeji さんのレス (2009/06/29(Mon) 16:42)
> 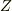 の展開は(1)(2d)ができれば,第一段階クリアです.
の展開は(1)(2d)ができれば,第一段階クリアです.
あ,この(2d)
>(2d) 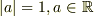 として
として 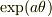 を
を 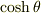 ,
, 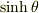 ,
,  で表せ.
で表せ.
ですが, 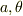 の役割を逆にした方が解り易くないでしょうか?
の役割を逆にした方が解り易くないでしょうか? 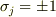 ですよね.
ですよね.
>出てきた拘束条件を幾何学的に解釈すれば終了です.
私は,この周辺でまだモヤモヤしてます.ので,興味深く拝見します.
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/29(Mon) 17:01)
そろそろしびれ切らした方も出てきたので,
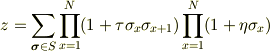
ここから,先にいきます.
まず
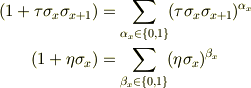
と書けます.これと,基本操作
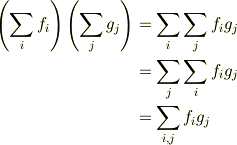
および,そこから一般化した,No.24333と同じ考え方

を使うと,大変だけど機械的にできる変形を経て
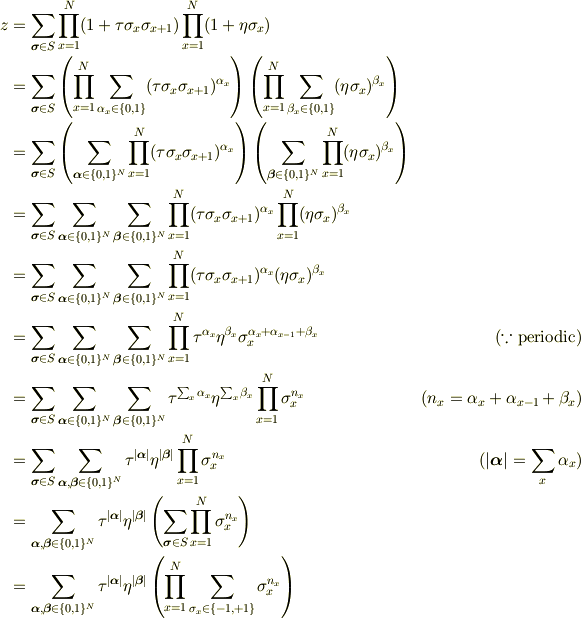
となります( 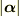 は
は 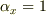 となる
となる 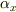 の個数です).
の個数です).
後は 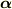 と
と 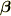 の拘束条件
の拘束条件
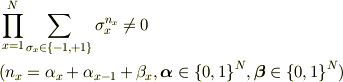
を計算し,その結果を幾何学的に解釈して, 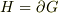 に書き直すだけです.
に書き直すだけです.
Re: 円卓モデルにおける対称性と相関関数について
mNeji さんのレス (2009/06/29(Mon) 17:56)
> 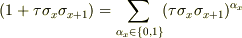
う〜む,気が付きませんでした.「1」を落とすのに苦労したのに!!!
ああ,その下に続く,和・積の軍団の整理を理解出来るのだろうか?--> 自分.
Re: 円卓モデルにおける対称性と相関関数について
mittwoch さんのレス (2009/06/29(Mon) 22:49)
つまり,No.24329で示した式に帰結するということですよね?
Re: 円卓モデルにおける対称性と相関関数について
mNeji さんのレス (2009/06/30(Tue) 05:23)
mittwochさん,結果としてせかしてしまった者で,済みませんでした.
>つまり,No.24329で示した式に帰結するということですよね?
そうだと思います.ここにご呈示された式は,私のような素人でもドキッとするほど興味深いものであり,さらにtoorisugari no Hiroさんの解説もそれに輪をかけて興味をそそられるものとして拝見しております.
逆に言えば,とても素晴らしい講義を受けられていると感じます.できれば,これからも,この講義で判らない点が在ったら,ここでご質問くださると嬉しいです.
なお,これまでのご質問の中で解決していない部分がありましたら,是非とも解決しきるようにされることをお勧めします.私の場合,次の変形;
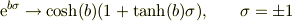
で悩みました.何度も計算しているうちに,確からしいと感じています.しかし,それが数学的に厳密に正しいのか,どこまで一般的な式と言えるのかを理解し切っていないのが現状です.でも,双曲線関数の面白さには驚きました.
恐らく,多くの動物ハンドル名の方々もこの問題に興味を持たれているので,ぜひとも質問を貫徹される事をご期待しております.
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/06/30(Tue) 11:52)
おいてけぼりも可哀想なので
> (2d) 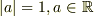 として
として 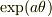 を
を 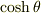 ,
, 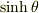 ,
,  で表せ.
で表せ.
変更しましょう.
(2d') 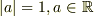 として
として
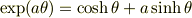
であることを(2b)(2c)より示せ.
これと(1)とで最初の変形はクリアですね.
Re: 円卓モデルにおける対称性と相関関数について
mittwoch さんのレス (2009/06/30(Tue) 22:35)
なるほど.
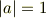
とは,すなわち
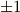
のことだったのですね. つまり,結果的に,
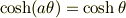
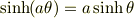
ということですね.
ここで,いきなり飛んで申し訳ないのですが,
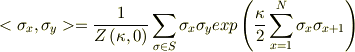
が
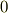
となることが分かりました. ここで,この期待値とは,何を表しているのでしょう? また,期待値からある確率を求めることは可能なのでしょうか?
Re: 円卓モデルにおける対称性と相関関数について
toorisugari no Hiro さんのレス (2009/07/01(Wed) 10:08)
> ここで,いきなり飛んで申し訳ないのですが,
> 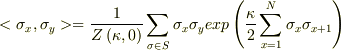 が
>
が
>  > となることが分かりました.
> となることが分かりました.
答えだけ書かれても欲求不満になる方もいらっしゃいます.あなたが情報を必要なように他の方も必要です.導出過程を説明してください.
ついでに 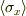 ,
, 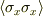 の値(+導出過程)も分かれば教えてください.
の値(+導出過程)も分かれば教えてください.