マルコフ連鎖についての問題なのですが..
マルコフ連鎖についての問題なのですが..
half tone guy さんの書込 (2009/06/20(Sat) 11:06)
はじめまして,大学1年生の者です.
大学の講義でどうしてもわからない問題があります.
「Ω状態のマルコフ連鎖においてRを遷移行列とするとき,詳細つりあいの条件,
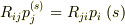 が成り立つとき,
が成り立つとき,
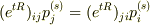 が成り立つことを証明せよ.」
という問題なのですが,講義中に習ったことを用いて式変形してみたのですが,
どうしても証明できません.
講義で習った証明に使えそうなものは,
「指数関数で累乗の位置に行列があるときのTylor展開の方法」
「マルコフ連鎖における,マスター方程式」
「
が成り立つことを証明せよ.」
という問題なのですが,講義中に習ったことを用いて式変形してみたのですが,
どうしても証明できません.
講義で習った証明に使えそうなものは,
「指数関数で累乗の位置に行列があるときのTylor展開の方法」
「マルコフ連鎖における,マスター方程式」
「 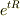 は時間をt進める行列」
です.
僕は最初に
は時間をt進める行列」
です.
僕は最初に 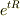 をTaylor展開して,それから最初の条件式を
使って証明しようとしました.
証明の仕方,あるいは証明の方向性を指摘してもらえたらありがたいです.
よろしくお願いします.
をTaylor展開して,それから最初の条件式を
使って証明しようとしました.
証明の仕方,あるいは証明の方向性を指摘してもらえたらありがたいです.
よろしくお願いします.
Re: マルコフ連鎖についての問題なのですが..
toorisugari no Hiro さんのレス (2009/06/20(Sat) 17:04)
を遷移演算子(
)としましょう.
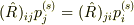 ならば,
ならば,
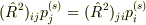 ,
, 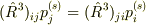 ,
,  が成り立つことを示したらいいのでは?
が成り立つことを示したらいいのでは?
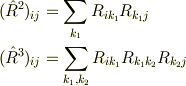
ですよね.
Re: マルコフ連鎖についての問題なのですが..
half tone guy さんのレス (2009/06/20(Sat) 18:42)
返信ありがとうございます!
おかげで証明することができました.
しかし,もう一つ疑問が,,,
結局示した等式の左辺,および右辺は一体どのような確率を表しているのでしょうか?
僕は「 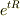 が時間をt進める行列だから,左辺と右辺はそれぞれ,マルコフ連鎖が定常分布に落ち着いてからt秒後に
が時間をt進める行列だから,左辺と右辺はそれぞれ,マルコフ連鎖が定常分布に落ち着いてからt秒後に 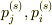 にいる確率」と考えているのですが,どうにも短絡的すぎると思えて仕方ありません.
重ね重ねの質問で申し訳ないんですがよろしくおねがいします.
にいる確率」と考えているのですが,どうにも短絡的すぎると思えて仕方ありません.
重ね重ねの質問で申し訳ないんですがよろしくおねがいします.
Re: マルコフ連鎖についての問題なのですが..
toorisugari no Hiro さんのレス (2009/06/20(Sat) 19:36)
そもそもの 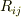 の定義は何ですか?
の定義は何ですか?
時刻  に状態
に状態 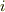 にいる確率を
にいる確率を 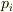 ,時刻
,時刻 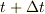 に状態
に状態 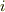 にいる確率を
にいる確率を 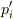 とあらわすとします(定常とは限りません).
とあらわすとします(定常とは限りません).  を微小として
を微小として 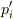 は
は 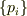 と
と 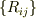 (あるいは
(あるいは 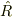 )でどう表現できるか考えてみてください.
# 当然時間的に一様なマルコフ連鎖をかんがえてます.
)でどう表現できるか考えてみてください.
# 当然時間的に一様なマルコフ連鎖をかんがえてます.
Re: マルコフ連鎖についての問題なのですが..
half tone guy さんのレス (2009/06/21(Sun) 11:38)
返信ありがとうございます.
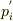 =(1- ?tΣ
=(1- ?tΣ 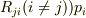 でしょうか?
この等式すら自信がないうえに,
でしょうか?
この等式すら自信がないうえに, 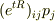 がどんな確率を表すかまったくわかりません.
もう少しヒントをいただけませんか?
がどんな確率を表すかまったくわかりません.
もう少しヒントをいただけませんか?
Re: マルコフ連鎖についての問題なのですが..
toorisugari no Hiro さんのレス (2009/06/22(Mon) 11:21)
# 私もよく分かっていないので,間違っていたら,よろしく.>識者の方
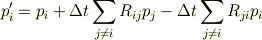
ではないでしょうか. これと
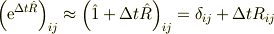
をくみあわせると関係式が出ませんか?
Re: マルコフ連鎖についての問題なのですが..
half tone guy さんのレス (2009/06/22(Mon) 21:56)
出てくる関係式は
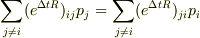 であっているでしょうか?
それから,示した式が何を表すのかは,やはりさっぱりわかりません.
であっているでしょうか?
それから,示した式が何を表すのかは,やはりさっぱりわかりません.
Re: マルコフ連鎖についての問題なのですが..
mNeji さんのレス (2009/06/22(Mon) 23:02)
half tone guyさん,横から失礼します.
門前の小僧モードですが, 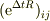 は言うならば,複数のパスを通って,j→k1→k2→...→iにいく確率を示すのではないでしょうか.
は言うならば,複数のパスを通って,j→k1→k2→...→iにいく確率を示すのではないでしょうか.
すると,左辺は,ある時刻tいるj状態からi状態への遷移確率の総和ですから,結局, 時刻t〜t+Δtの間に,他の全ての状態からi状態に流入する確率を示すのではないでしょうか,
逆に,右辺は,あるi状態から,時刻t〜t+Δtの間に,他の全ての状態へ流失する確率を示すと思えます.
両者をあわせて,i状態は動的な平衡を示していると,考えられそうですね.当てずっぽうですが...,面白そうですね.
Re: マルコフ連鎖についての問題なのですが..
toorisugari no Hiro さんのレス (2009/06/23(Tue) 15:11)
> 出てくる関係式は
> 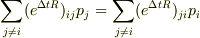 > であっているでしょうか?
> であっているでしょうか?
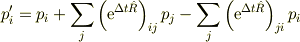
ですね.これをテーラー展開したものがmNejiさんの描像にあたります.
ここで平衡状態では 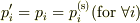 が成り立つので,これを代入すると求める式が出てきます.
が成り立つので,これを代入すると求める式が出てきます.
Re: マルコフ連鎖についての問題なのですが..
half tone guy さんのレス (2009/06/23(Tue) 18:55)
toorisugari no Hiroさん,mNejiさん,返信ありがとうございます.
なるほど,j=iにする必要はないんですね.
出てくる関係式は,平衡状態の条件を使って,
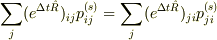 ですよね.
この関係式と,
ですよね.
この関係式と, 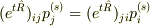 とどのように結びつければいいんでしょうか?
とどのように結びつければいいんでしょうか?
 を微小にしたときの
を微小にしたときの  のときにしか,上の関係式は成り立たないと思うのですが.
のときにしか,上の関係式は成り立たないと思うのですが.
Re: マルコフ連鎖についての問題なのですが..
toorisugari no Hiro さんのレス (2009/06/23(Tue) 20:38)
と表しましょう.微少量
に対して
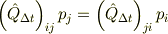
が成り立つなら, 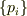 が平衡状態の式を満たすのはあきらか.
また,同じ条件の下で,Qのn乗の関係式
が平衡状態の式を満たすのはあきらか.
また,同じ条件の下で,Qのn乗の関係式
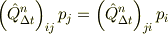
が任意の自然数  で成り立つので,
で成り立つので,
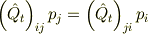
が任意の  で成り立つのも自明.
で成り立つのも自明.
Re: マルコフ連鎖についての問題なのですが..
toorisugari no Hiro さんのレス (2009/06/25(Thu) 11:26)
>> もしかして
>>  >> という条件がありますか?
>> という条件がありますか?
> はい.確かにその条件があります.
前提条件をすべて出してもらわないと問題は解けません.まだ,他にないですか?
Re: マルコフ連鎖についての問題なのですが..
toorisugari no Hiro さんのレス (2009/06/25(Thu) 13:48)
だと議論がずいぶん簡単に,かつ,つじつまが合うようになりますね.
# そもそも,ちゃんと  の定義を述べてもらえれば,簡単だったのに....
の定義を述べてもらえれば,簡単だったのに....
先に挙げた式
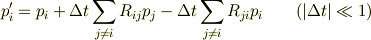
は(確率が意味を持つための条件の一つである)ノルム保存則 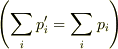 を満たしますが,
を満たしますが,
> 返信ありがとうございます. > |6dc021bab519a66a3966219996835e14| =(1- ?tΣ |ee4ae2ba9ba0702580404a9130b7830d| > でしょうか?
の
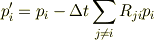
は 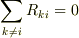 もしくは
もしくは 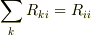 を任意の
を任意の 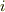 で満たさないとノルム保存則を満たしません.
で満たさないとノルム保存則を満たしません.
ただし, 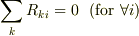 が前提条件になるなら,第一の式は簡単な
が前提条件になるなら,第一の式は簡単な
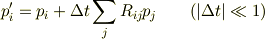
になり(当然保存則を満たします),ここから
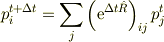
が任意の  に対して成り立ちます.
に対して成り立ちます.
ここから,平衡状態の議論も導けます.
問題: ノルム保存則により
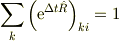
ですが,これを 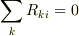 から証明してください.
から証明してください.
