Electra さんの書込 (2009/06/08(Mon) 01:35)

Electraです．よろしくおねがいします．

このサイトでガリレオのピサの斜塔の実験の部分をよんでいたのですが， ＞確かに質量が大きいと重力も大きくなりますが，同時に物体を動かすために必要な力も大きくなるの ＞で，結局落ちるスピードは同じになるのです． という部分があります．「質量が大きいと重力も大きくなる」というのはわかるのですが， 「同時に物体を動かすために必要な力も大きくなる」という部分がわかりません． この”力”とはなんの力でしょうか． てっきり重力がものを動かしてるものだと思っていました．

どなたか教えていただけますでしょうか．

Yokkun さんのレス (2009/06/08(Mon) 13:27)

Electraさん，こんにちは．

「物体を動かすために必要な」に要点があります． 質量が大きくなる・・・物体が受ける重力が大きくなる． 質量が大きくなる・・・物体の「慣性」＝運動状態を保とうとする性質が大きくなる．

この「慣性」の大きさを「動かすために必要な力」と表現したわけです． 運動方程式質量×加速度＝力

質量が大きくなると，同じ加速度を生じさせるのに「必要な力」が大きくなるという意味ですね？

質量が大きくなると，重力が大きくなる・・・重力は質量に比例する 質量が大きくなると，同じ加速度を生じさせるのに「必要な力」が大きくなる（動きにくくなる）

「必要な力」が質量に比例して大きくなり，現実の力（重力）も質量に比例して大きくなったから，落ちるスピード（正確には加速度）は同じになる，といっているのです．くだいていうならば，質量がふえると受ける重力もふえるが，動きにくさもふえるので同じといいたいわけです．

mNeji さんのレス (2009/06/08(Mon) 18:07)

Electraさん，別意見を述べさせて頂きます．

ピサの斜塔の実験というのはどの程度の精度の実験か知りませんが，どうして空気抵抗が無視出来るのか，私には判りません(笑)．

さて，ピサ斜塔も含めて，我々が住んでいる地表近くは，近似的に静止した系であり，静止系とか慣性系といわれます．そのような系の中を運動する物体を決めるのが，ニュートンの運動法則です．

私は，この説明に「慣性力」という言い方をするのは「誤解を生じ易い」と考えています．では，どうするか？，が問題です．私としては下記の様に考えます；

適当な静止系から，ある小さな物体の運動をみると，

「その物体の運動量の時間変化」＝「その物体に加わる全ての力の総和」 「その物体の運動量」＝「その物体の質量」x「その物体の速度」 「その物体の速度」＝「その物体の位置の時間変化」

私は，「雨粒」が近似的に一定速度で落下する現象を実験的に示し，日常的な物体の落下と対比させて考えると良いのでは無いかと思っています．

Yokkun さんのレス (2009/06/08(Mon) 20:00)

mNejiさん，Electraさん，こんばんは．

>ピサの斜塔の実験というのはどの程度の精度の実験か知りませんが，どうして空気抵抗が無視出来るのか，私には判りません(笑)．

ガリレオがピサの斜塔から落下の実験をしたというのは，没後ガリレオの弟子が挿入した逸話ですね．私は，ガリレオならやりかねないとも思うのですが，地上50ｍを超える高さですから，注意深く測定すれば鉛球の落下にも空気抵抗の影響が出るでしょう．ただし，ガリレオにとって比較する対象（鉛よりも重いもの）は準備できないかもしれませんが．

「力学」のガリレオ・ガリレイの節を読まれてのご質問ですので，質問された部分がピサの斜塔での実験についての記述でなく，空気の抵抗が無視できる条件での自由落下のことをさしていることはおわかりでしょう．空気の抵抗についてはガリレオも概ね正しくその存在を評価しており，それが無視できるような条件では，落下のはやさが質量に無関係であることをきわめて正確に外挿しているのです．したがって，ここで空気抵抗の下での「終端速度」の比較を持ち出すのは妥当ではありません．

>この説明に「慣性力」という言い方をするのは「誤解を生じ易い」と考えています．

「必要な力」を「現実の力」（重力）と対比させたので，誤解を招いたかもしれませんが，「必要な力」はもちろん「慣性力」のことではありません．物体の質量m，加速度をa，受ける力をFとすると，運動の第２法則は ma = F（質量×加速度＝力） と書けるわけですが，この一般的抽象的な力Fが物体に加速度aを生じさせるのに「必要な力」です．質量が大きいと同じ加速度を生じさせるのに大きいFが必要．つまり質量の大きさは物体の動きにくさ（止まりにくさ）＝慣性の大きさを示しているということをいっているわけです．ところが，今「現実の力」が重力でこれがまた質量に比例している．一般的抽象的な力Fは，自由落下の場合に F = mg（gは重力加速度とよばれる定数） と現実的具体的な力に書き換えられます．

物体が受ける力が質量に比例し，物体の動きにくさ（止まりにくさ）＝慣性がこれまた質量に比例する．したがって，結果として得られる加速度が a = g となって，質量に無関係になるというのが，この場合のElectraさんが引用された部分の主旨です．

以上の議論で慣性力は必要がないばかりか，混乱のもとですね．この点ではmNejiさんに全く同感です．

Electra さんのレス (2009/06/09(Tue) 08:12)

Yokkunさん，mNejiさん

ありがとうございます．

a=gの説明は目からウロコでした． 「gは一定なので地球上ではma=Fの法則の下，mに応じてFが増加する」 と理解しました．

一方でそもそもの疑問の発端である ＞確かに質量が大きいと重力も大きくなりますが，同時に物体を動かすために必要な力も大きくなるの ＞で，結局落ちるスピードは同じになるのです． は，地球上ではmg=Fだが，そのFはma＝FのFなので，結果aはgと同じになるということと理解しました．（落ちるスピードが同じという事は，加速度が同じという事と同じですよね？）

このの２つの理解に矛盾があるように感じました． 「物体を動かすために必要な力も大きくなるので，結局落ちるスピードは同じになる」 のでしょうか，それとも 落ちるスピードが同じだから物体を動かすために必要な力も大きくなるのでしょうか？ 結局何が落ちるスピードを同じにしているのかがわかりません． 現在の僕の理解では，落ちる速度が同じなのは単純ににgが一定だからだといった具合です．

ちなみに一定である重力加速度gの発生源は地球の質量に基づく引力という理解でよろしいでしょうか？

mNeji さんのレス (2009/06/09(Tue) 08:33)

私は，頭が固いので，オウムのように繰り返し同じ事しか書けない事をお許し下さい．

私は，「慣性力」という言葉そのものに強い違和感を持ち続けています．

特に，静止系で見た時に，「外力の総和がセロ」な時に，その物体が一定の速さを保つ時に，それを「慣性力」のお蔭だとするような説明です．

＃遠い話ですが，この点について，高校の時に教師と論争したものの，納得ができず，以来，高校での物理は独学となりました．

本質的なのは， ・「力」が作用するのは「運動量の時間変化」である． ・「力」が作用するのは「速度」では無い！

翻って，電車に乗って，雨が降っている時に「窓吹き付ける雨粒の流れが，ほぼ一様に平行に流れている」のを見れば見る程，雨粒が等速運動をしていることは，直感的に明らかな事だと思います．

ところが，「ピサの斜塔」の実験では， ・空気抵抗が無視出来るなら， ・落体はすべて，「重力加速度とおなじ加速度で運動する」 と言われると，「雨粒の経験則」と多いに矛盾するので，驚愕したのだと思います．むしろ，積極的に「空気抵抗」の効果を実験や映像資料などで説明することが重要だとおもいます．

結局，現在の高校教育では； ・数学的準備をしないで， ・力学を自然な流れで理解をさせる． ということは不可能だろうと思う様になった訳です．

まあ，世の中には，高校の物理教育と相反する捉え方をする者もいるということです．失礼しました．

Yokkun さんのレス (2009/06/09(Tue) 08:36)

まだ，「物体を動かすために必要な力も大きくなるので，」で混乱があるようです．これは，

「質量が大きくなると，その慣性も大きくなるので」

と読みかえてください．「必要な力」に要点をおかれると意味不明です．質量が大きくなると，その速度を変えるのにより大きな力が必要になる，つまり物体の慣性（動きにくさ，止まりにくさ）が大きくなるという意味です．

自由落下の場合，運動方程式より ma = mg ∴ a = g になって，質量にかかわらず加速度が同じになるということに過ぎません．この点は，ご理解いただいたようですね？

>ちなみに一定である重力加速度gの発生源は地球の質量に基づく引力という理解でよろしいでしょうか？

その通りです．万有引力定数G，地球質量M，地球半径Rとして， g = GM/R^2 と書けます．これに物体の質量をかけると，地上の重力mgが地球と物体の間の万有引力であるという式が得られます．

＃mNejiさん，私は「慣性力」とはひとこともいっていませんし，「慣性力」について触れてもいません．完全な誤解です．

>・・・むしろ，積極的に「空気抵抗」の効果を実験や映像資料などで説明することが重要だとおもいます．

その通りですね．ですから，ガリレオも周到に空気抵抗の思考実験と実際の実験をもとに，それを無視できる理想化のもとでの「同じはやさでの落下」の議論を展開しています．空気抵抗に対する深い洞察がなければ，この理想化の意義を理解することはできないのだと思います．かぎしっぽでもそのことについてはきちんと書かれています．現実の運動は複雑に過ぎて，一見手におえません．その手におえない現実の落下運動の複雑さから，空気抵抗という要因をひとまずとりのぞくという理想化を大胆に推し進めたところに，ガリレオの真骨頂があります．なお，ここで「はやさ」といっているのは，ガリレオの表現を借りたもので，かぎしっぽでも「スピードは同じになる」といっていることと同等です．速度は刻々と変化するけれども，その瞬間瞬間での比較では質量の違いによって差が出ませんよといっているわけですね．

>静止系で見た時に，「外力の総和がセロ」な時に，その物体が一定の速さを保つ時に，それを「慣性力」のお蔭だとするような説明です．

これは，明らかに「慣性力」概念の誤用で，mNejiさんに異議ありません．「力」が入るだけで全く誤った表現になりますね．ガリレオ以前の「運動する物体に込められた力」というイメージでしょうか？ ガリレオも初期のころには似たような記述が見られたと思いますが，相対性原理の確立以降は脱却したようです．

mNeji さんのレス (2009/06/09(Tue) 10:45)

私は，ガリレオ・ガリレイさんの研究過程を勉強した事がありませんので，あまり詳しくはコメント出来ません．

しかし，余りに「ピサの斜塔」の話から，物事の理解を始めるのは誤解のもとではないか？，といった感想です．

むしろ，「バネばかり」と「重力ばかりとしての天秤」などの静止力同士の釣り合いなどを経て，質量と力の関係を組み立てた上で，運動方程式にはいれば，「慣性」とか「慣性の力」とか「慣性力」といった難しい言い方を必要としないのではなかろうかという観点です．

その意味で「慣性」という言葉を初学者の方々にどのように説明するのはを，私は知りませんし，知りたいとも思いません．

勿論，物理学史とかの観点で，詳しい研究の価値は在ると思いますが，高校までの流れでは「慣性」に関わる説明は払拭しても，何らの障害もないと愚考しています．

Yokkun さんのレス (2009/06/09(Tue) 13:14)

>「慣性」に関わる説明は払拭しても，何らの障害もないと・・・

私は，逆に「慣性」（「慣性力」ではなく）を理解することが運動の法則を理解する土台だと考えています．

運動方程式は運動の状態の変化を表す「加速度」とその原因である「力」の比例関係に終わるものではありません．かならず「質量」との関係がつきまといます．この「質量」に「慣性」の大いさの意味をとらえることこそ，運動の法則の本質的な理解なのではないでしょうか？

私たちには「物体が動き続けるには力が必要である」との経験にもとづく強固な「常識」があります．力が必要なのは実際には摩擦や抵抗があるからで，物体が速度を維持するためにはそれとつりあう力が必要であるということなのですが，摩擦や抵抗がなくとも速度の維持に力が必要だとの思いこみが必ずつきまといます．これを払拭するには，物体が「質量」をもつことそれ自体で，運動状態の変化に抵抗する性質＝「慣性」があるという理解が必要です．このことを土台にすえなければ運動の法則に対して，本質的な理解に到達することはできないと思います．

「慣性」を「物体に込められた力」とする誤りを乗り越えて，力と慣性とを切り離して独立の存在としたところに力学の発展があり，少なくともこの部分は初学者の学習にとっても土台に据えるべきものと思います．「慣性力」と「慣性」とは関わりはあるものの，同列に扱えるものではないと思います．ちなみに「慣性力」は「物体に込められた力」という誤りとは全く関係ありません．

>「外力の総和がセロ」な時に，その物体が一定の速さを保つ時に，それを「慣性力」のお蔭だとするような・・・

もし，この「慣性力」がそのものの意味として使われていると思われるのであれば，それはとんでもない「慣性力」に対する誤解です．これこそは「込められた力」に相当するものですね？

いずれにせよ「慣性力」をぬぐい払いたいがために，「慣性」も「払拭」されてしまうのでは，大根の汚れ（私は「慣性力」を「汚れ」とは思いませんが）をおとさんとして大根を流失するようなものです．古今東西を問わず，力と運動の学習は質量＝慣性の大いさの理解に始まるといってもよいと思います．重力質量に加えて，慣性質量の発見こそが運動力学の土台です．

ヒノッキー さんのレス (2009/06/09(Tue) 15:08)

どうも，ヒノッキーです． Yokkunさんと，mNejiさんの， 慣性力（Yokkunさんは慣性力ではなく，慣性だが） に関する議論，第２ラウンドが始まったようですね．

Electraさんの質問に，僕なりに答えてみようと思い， 途中参戦させていただきます（笑）

通常，大きさｍとＭの二つの物質を同じ大きさの力Ｆで押すと， 加速度は変化し，二つのスピード（この場合は不適切かと思いますが・・・） が異なることになります．

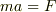
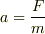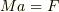
と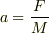， というようになり，ｍとＭの大きさは異なるので， 加速度が違ってきます． おそらくYokkunさんはこの加速度の違いを利用して， 質量が大きいものほど，その場にいようとする性質が強い． ということを説明したかったのではないのでしょうか． （慣性の法則）

では，重力（地球上で近似された．）ではどうなるのでしょうか． 万有引力により，すべての物体は引き合っており， その引き合う力は，質量の大きさや距離で決まってきます． そして以下の式により， 地球の地上付近では同じ加速度であるとみなせるのだと， 考えています．

万有引力の公式を下に記します． （質量ｍの物体に関する運動方程式です．）

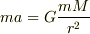
ここで，Ｇは重力定数（一定の値です．）， ｒは２物体の距離（今回は質量Ｍの地球の中心から質量ｍの物体の間の距離です） を表しています． この式の右辺が，地球の表面付近では近似されてｍｇとなっているのです．

なぜなら，Mは地球の質量なので一定で， ｒも，地球の表面付近なら近似的に同じ値とみなせるからです． （このｒは，月と地球や人工衛星と地球などの距離になってから， 効果がでてくる．）

Ｍ，ｒ，Ｇは定数なので，この組み合わせをｇとしており， 加速度が等しくなることを示しています． これより，地上付近ではｇという一定の加速度によって 物体が引きつけられると僕は考えています．

＞結局何が落ちるスピードを同じにしているのかがわかりません

答えは，「地球の質量が一定で，距離が近似的に一定とみなせるから」 加速度を同じにしている，です．（ハズれてたらごめんなさい．）

ヒノッキー さんのレス (2009/06/09(Tue) 16:02)

mNejiさんの意見はなかなか興味深いので，僕なりの考えを載せておきます．

まず，慣性と慣性力の違いですが，

「慣性」・・・物体に力が働かないとき， そのままの運動状態でいようとする性質． （静止しているならそのまま，運動しているなら等速直線運動）

「慣性力」・・加速系で見たときの見かけの力． （電車の中の吊革や，車がカーブしたときの遠心力）

と，定義されていたと思います． 慣性と慣性力は全く違うのです．

慣性力は，加速系ではなく，慣性系で考えればいいだけの話で， わざわざ慣性力を考えるのは難しい，という意見には大いに賛成です．

一方，慣性とは運動方程式が，ｍa＝〜になっているためには大前提としなければいけない性質だと考えています．

経験則から，質量が大きいものほど動かしにくく （前の状態を保とうとする性質が強い） 質量が小さいものほど，動かしやすい． （前の状態を保とうとする性質が弱い） ということが知られています．

＊性質が強い，弱いとは，独自の表現ですので， ＊語弊があったらすみません． ＊ただ，力が大きい，小さいとすると慣性力と混同してしまうので ＊こう表現しました．

この事から，運動方程式の左辺はｍaとなったのではないでしょうか？ 慣性の性質はとても重要なものです．

・・・もっとも，似たような名前だし，あながち無関係ともいえないので よく混同してしまいますが． 「慣性の力」などと言われたら混同してしまうのも無理はないです．

「慣性」と「慣性力」・・・． もう少し区別のしやすい名前にしてほしいですね．

なんとなく さんのレス (2009/06/09(Tue) 16:55)

なんとなくです． 元々のElectraさんの疑問は，Yokkunさんがさらりと書かれているのですが，（慣性）質量と（重力）質量の混同にあると見受けられます．勿論現在ではこれら両者の間に違いはないか，比例定数が１であるため実質的に差が無くなり，単に質量と呼ばれているわけですが．その意味で質量を分かり易く説明しておく必要があると思います． ピサの斜塔実験の当時には物体は”重さ”（重力と切り離せない）で区別されていたのだと思います．例えですがまったく同じ大きさの鉄球とアルミ球を考えれば，鉄球の方がずっと重く，経験的に”より重い”→”より強く引かれる”→”より早く運動する”という連想が自然でしょう．しかし，実験は期待を裏切り，”重さ”によらなかったのです．勿論ここでは空気抵抗など些末な擾乱は無視できます．ガリレオは斜面の運動を通じ，更に水平にして慣性の法則に行き着いたという説がありますが，それこそ重力と切り離して運動を考える方便です．しかし我々は宇宙空間を知っているので，そこで前者２物体を動かしましょう．当然無重力で”重さ”はありません．しかし，そこでは同じ加速度を得るには鉄球の方が大きな力が要ります．このとき鉄球とアルミ球には何の違いがあるのでしょう．その何かの比例定数を（慣性）質量ｍと言います．それが，Ｆ＝ｍａという運動方程式です． 一方，地上では引力により物体に”重さ”が生まれます．上の意味でこの比例定数を（重力）質量Ｍと言いますが，上述から分かるように本来この２つは無関係だったのです． しかし，地上では力として重力を力として与えてこの運動方程式も満たすとすれば，ｍ＝Ｍであれば，結局運動方程式から質量が消え，同じ加速度ｇのみとなります（ここは理解してお出ででしたね）．

元にもどれば，質量ありきの文章であるため， >「質量が大きいと重力も大きくなる」→「同時に物体を動かすために必要な力も大きくなる」 の２番目の文は，特に別な力を表しているのではなく，運動方程式に現れる，いわば”概念”としての力です．この２文はお互いが比例し，結果として同じ加速度になるという事を（スピードはそのある瞬間です）説明しているわけです．

ちなみに蛇足ですが，この慣性質量と重力質量の比例定数は近年まで測定され続けており，今のところ１（同じ）です．相対論の帰結でもありますが，絶対に将来もそうであるとは言い切れません（この話は極度に高度ですので深入りしません）．

mNeji さんのレス (2009/06/09(Tue) 19:36)

ヒノッキーさん，

本来のスレッドから離れて来ているとは思いますが，No.24099に関してコメントさせて戴きます．

＞（この前は省略） ＞と，定義されていたと思います． ＞慣性と慣性力は全く違うのです．

概ね，そのように考えています．

でも，一度運動方程式ベースに考えを展開する時には，「慣性の法則」を何度も持ち出されると，運動方程式には「慣性の法則」が含まれないかの誤解を生じ易いと考えます．

私は，以前の論議でもでましたが， ・適切な静止座標系を定め， ・現象に関与する力やトルクを過不足無く確認し， ・運動量の時間変化なり，角運動量の時間変化について，運動の式を立て， ・以後は，解くのに最適な座標系を使う という一連の作業のなかに，「慣性の法則」なり「作用反作用の法則」が自然とくy見込まれている，と考えます．

また「慣性系」という言い方も，初心者の時には，なにか特別な意味があるようで悩んだものです．やはり「静止系」なり「等速運動系」が解り易いですし，対応して「加速運動系」といったら紛れないと思います．

Yokkun さんのレス (2009/06/09(Tue) 20:05)

>「慣性の法則」を何度も持ち出されると，運動方程式には「慣性の法則」が含まれないかの誤解を生じ易いと考えます．

私が「持ち出した」のは「慣性の法則」でもありません．なんとなくさんが正確にまとめられたように，慣性質量としての質量＝慣性の大いさという質量の「もうひとつの」意味を強調したのですね．もちろん，慣性の法則は大いに関係するところですが，「慣性質量」は運動の法則＝運動方程式まで踏み込まないとその意味ははっきりしないですよね．

「慣性の法則」は第２法則に含まれるとされる向きは承知していますが，慣性系の存在仮定とする独自の意義を認める見方が，私にはしっくりきます．また「作用・反作用の法則」が自然と組み込まれているというのは，私にはその意味が量りかねます．これらの点はまたの機会にでも．

mNeji さんのレス (2009/06/09(Tue) 20:23)

Yokkunさん，

＞私が「持ち出した」のは「慣性の法則」でもありません．なんとなくさんが正確にまとめられたように，慣性質量としての質量＝慣性の大いさという質量の「もうひとつの」意味を強調したのですね．

すくなくともニュートンさんに限らず，ガリレイさんにしても，「物の量」の尺度として「天秤計り」による計量の概念はあったのではないでしょうか．まして現代の学生さんには質量が「天秤計り」や「バネ計り」などで計る事のできる量である認識は可能だと思います．

それを「慣性質量」と言い切ってしまうと「慣性？」ということになってしまうのではないでしょうか？むしろ積極的に「重量質量」とでも置いておいて，運動方程式の運用に理解が進んだところで，「慣性質量」と「重量質量」の概念的問題点を論議するので十分だろうと思う訳です．

Yokkun さんのレス (2009/06/09(Tue) 20:50)

mNejiさん，もちろん実際の概念の理解は経験に明らかな重力質量からでよく，「慣性質量」の概念を押し付ける必要はないのです．でも，質量が慣性の大きさをも示すということが運動方程式の内容的理解ということになるのではないですか？

「重いものは動きにくい」という経験と理解が，実は摩擦のため・・・というところにとどまっている「常識」を破らなければ，「動き続けるためには力が必要」という誤解から抜け出せません．mNejiさんが「運動方程式の運用に理解が進んだところで・・・」といってのけられるのは，実は物体の慣性に対する基本的な理解が完成していることを意味しているとは思いませんか？それは，言葉や概念としての「慣性」や「慣性質量」を知っているかということとは別の，内容的な理解という段階の話です．だからこそ，私は慣性の最も初歩的な表現として「動きにくさ，止まりにくさ」という言葉を併せて使っているのですよ．

mNejiさんが，運動方程式の運用に理解が進まれているのは「慣性質量」への内容的理解があるからとは思いませんか？運動方程式を運用できるということは，すでに身につけられているからなのです．

「慣性」の概念はmNejiさんがおっしゃるとおり奥深い内容を持っていますが，しごく基本的でもあります．ですから，小学校の段階でも「慣性」の言葉はないにせよ慣性概念に対する内容的な踏み込みは学習指導要領を見てみると運動エネルギーの形をとって現れているようです．「慣性」はごく基本的でありながらとても深奥で高度な概念なのだと思います．その高度な部分を知らないと運動の法則が知りえないなどと申し上げるつもりはもとよりないのです．mNejiさんが考えておられるような深い「慣性」概念のレベルの話ではなく，「はずみ」とも呼べるようなごく初歩的な理解が必要ということです．そして，それを重さとは別に「質量」に付随する特性のひとつとして新たに理解に付け加えることが必要ですよ，ということなんです．この点は共感していただけませんか？

mNeji さんのレス (2009/06/09(Tue) 21:32)

Yokkunさん，

私は，高校の教科書は試験の前の日にちょこっと眺めたくらいで理解していませんでした．その代り「PSSC物理」という本は丁寧に読んだ筈です．とはいえ，手元に無いですし，忘却の彼方に近いです．

ただ，うろ覚えですが，氷の台の上に物をすべらして，ストロボ写真を撮り，運動の写真を丁寧に解説していたような気がします．

また力の性質を，バネとか滑車付きの錘を組み合わせて，「重力」と「バネの力」，「力」と「変位」，「力」と「重さ」などの関係から，「運動量の時間変化外力によって引き出される」といった流れで解説したと言う気がします．

少なくとも「慣性」という言葉は出てこなかったと思います．ひょっとして，上の理解は，違っていて，その後にベクトル解析の本やファインマン物理などを読むうちに防衛的にそう考えたのかは判りません．

小学校・中学校では，理科の時間に， ・アイス・リンクに連れて行って，滑って転んだり， ・自転車で強く漕いで，ブレーキせずに止まるまで待たせたり ・プールで「水中歩行」と「蹴伸び」とで同じ3mを進む違いを実感させたり すれば，体感的に運動の理解が深まる様に思います．

ちなみに，私が中学生のころ後楽園遊園地で，大きな回転筒の側面に立ち，回転筒が廻りだすと共に，床が下がっても自分の体が壁に引っ付いたままで落下しない経験をしました．この時の驚愕はとても強く，「遠心力」は実在する！，という事を思い知りました．

＃その後，曲座標表示の計算で「遠心力」や「コリオリ力」が出て来たときは， ＃後楽園遊園地の回転筒を思い出しました．

自分の様に実験的に体感出来ないと理解が進まないのは勉強効率が悪いのだとおもいます．でも形式的に「慣性」を先に叩き込みというのは，やはり納得できません．でも，工夫した流れを構築して，解り易い教育プログラムを作るトライアルまでを否定する積もりはありません．

Yokkun さんのレス (2009/06/09(Tue) 23:23)

>この時の驚愕はとても強く，「遠心力」は実在する！，という事を思い知りました．

とてもよくわかります．私は数年前，部屋全体が動き傾きを変えることで加速するコースターのバーチャルリアリティを映像とともに体感する遊園地のアトラクションを試してみて，重力が慣性力と等価である事を実感しました．

>実験的に体感出来ないと理解が進まないのは勉強効率が悪いのだとおもいます．

いいえ，上の遠心力の話のように，実体験に勝る学びはないですよ！わかったつもりで体験してぎゃふんとくることも多いですよね．

ただし，物理学においては素朴な体験が時として誤った理屈または「常識」の源になることは肝に銘じておくとよいかもしれません．「常識」の壁を乗り越えて，理論を獲得した上で実体験すると，さらに感動します．

>でも形式的に「慣性」を先に叩き込みというのは，やはり納得できません．

うーん．私がそういうのが効率的なのだと思っているとお考えなのですか？とんでもない誤解です．「慣性」こそは体験が先行すべきものだと私は思います．私が唯一この点で「叩き込み」が必要だと思うのは，体全体を使って遊びまくっている子どものころに，その体験，体感をりくつとして跡付けてやることです．「車は急に動けない，止まらない」というレベルでいいんです．

物理に熱中する私たちは，まるで「子ども」です．考えてみれば，野山をかけめぐる実体験の貧しさが日本の理科教育の困難の元凶のひとつではないのでしょうか？そして，根っからの科学者と呼べる人は子どものころからの体験にもとづく素朴な疑問を，あきらめずに持ち続けた人であると思うんです．私も末席でいいからそうありたいと思うんですね．それだけに遊びの条件をせばめてしまっている日本において，初等理科教育の悩みは深いんだと思います．

mNeji さんのレス (2009/06/10(Wed) 02:34)

＞ただし，物理学においては素朴な体験が時として誤った理屈または「常識」の源になることは肝に銘じておくとよいかもしれません．「常識」の壁を乗り越えて，理論を獲得した上で実体験すると，さらに感動します．

具体例を挙げて頂きたいです．少なくとも，通常のニュートン力学の範疇で，「常識」と「理屈」とに乖離があった事例を私は知りません．あ，ただ流体力学は除きますが...．

＞「車は急に動けない，止まらない」というレベルでいいんです．

このレベルだったら，「慣性の法則」と結びつける必然性は無いと思います．むしろ何も力を受けないで静止状態(等速運動の一例)にあれば，力が掛からない限り運動量も変わらないという日常感覚と一致しています．

むしろ，その状態から外力が加わる場合です．仮に自動車に乗っていて，初期状態に車が静止状態(等速運動の一例)にあれば，自分は車から力を受けずに，静止したままで，其れを「慣性の法則」と結びつけて，容易に理解出来ます．

では，車が前向きに加速したときを考えると気に，「慣性の法則」を知っていることから，どのような理解を生みだせるのでしょうか？初学者は，正にこの点で躓く筈です．私には，「慣性の法則」は何も教えてくれないと思います．結局，正しく理解した上で，運動方程式がその回答を出せるのだと，思います．

私は，歳を取ってリハビリテーションの為に，水泳とか，太極拳とか，バレエ系の柔軟運動をするようになりましたが，自分の体の運行を，常に第三者的に外部の静止系から見た観察を出来ます．と同時に，運動者として加速系としての自分の体勢感覚を感じます．

この場合でも，「慣性の法則」という言葉を使う事無く，至ってスムーズに観察や知覚をする事ができて，困りません．ただし，最近，興味深いとおもうのは，自分自身が地球ゴマのような大きなジャイロ系に入って，体を複雑に回転できたら，どんな感覚が生まれるのか，と言う点に興味があります．

Yokkun さんのレス (2009/06/10(Wed) 09:17)

>具体例を挙げて頂きたいです．

すでにいくつかの具体例をあげています．たとえば，「重いものほどはやく落ちる」．空気抵抗を考えれば・・・とはいいますが，３ｍの天井から落としたゴルフボールとピンポン球と着地時にどのくらい差がでると思いますか？視認できる差は出ません．次いで，「動き続けるには力が必要」．摩擦のない台車に摩擦のある物体を引きずらせます．一定の速度で引くとき，台車が手から引かれる力と，引きずっている物体から引かれる力とどっちが大きいか．多くの初学者は手が引く力が大きいと思っている．mNejiさんは，ずいぶん高度なレベルで問題をとらえていらっしゃいます．私が強調しているのは，全くの初学者のレベルです．

>このレベルだったら，「慣性の法則」と結びつける必然性は無いと思います．

「慣性の法則」について初学者を対象に他にどんなレベルの理解がありうるとおっしゃられるのか，私にはよくわかりません．「車は急に動けない，止まれない」・・・このレベルこそは，「慣性の法則」の最も初歩的で重要な理解ではないですか？そして，力がつりあっている状態の「慣性の法則」の理解は第2法則に先行すべき独自の意義があると思います．「力が掛からない限り運動量も変わらないという日常感覚」といいきれるmNejiさんの常識は決して初学者のものではありません．「動き続けるのに力はいらない」・・・mNejiさんが「日常感覚」と言い切るこの認識こそが私には第2法則に先行して絶対必要だと思えるのです．多くの場合，初学者はこの認識に立てていないのです．

>車が前向きに加速したときを考えると気に，「慣性の法則」を知っていることから，どのような理解を生みだせるのでしょうか？初学者は，正にこの点で躓く筈です．私には，「慣性の法則」は何も教えてくれないと思います．

「慣性の法則」には，mNejiさんも第2法則への包含を示唆されているように，第2法則の理解への準備があります．「動き続けるのに力はいらない」のですから，合力がゼロでなければどうなるのか，と認識を発展させることができます．「力の原理」＝つりあわない2力を逆向きに受けるとき，大きい力の方へ動き出す．こうして，「慣性の法則」を土台にして第2法則へと昇っていく・・・これが無理のない認識の順序ではないでしょうか？

>「慣性の法則」という言葉を使う事無く・・・

「慣性力」のアクロバティックな乱用を批判される点は全く理解できますが，どうしてそれとはレベルも内容も全然違って初歩的な「慣性の法則」の言葉と概念を不要のものと捨て去ることができるのか．私にはどうしてもわかりません．先にもいいましたように，mNejiさんは深奥な「慣性の法則」の高いレベルを私が初学者に要求していると勘違いされているのではないかと思います．「慣性の法則」に独自の初歩的・教育的な意義を認めないというのは，たとえば力のつりあいも加速度ゼロの運動方程式でいいのだというのと同じです．力の発見やつりあいの概念を知らずにいったい第2法則をどう理解せよとおっしゃるのか．

mNeji さんのレス (2009/06/10(Wed) 14:40)

Yokkunさん，

＞３ｍの天井から落としたゴルフボールとピンポン球と着地時にどのくらい差がでると思いますか？視認できる差は出ません．

ところが，日常的に見ることができる「塵」とか「猫の毛の塊」などはフワフワしますし，前回書きましたが「雨粒」はほぼ等速で落下して来ます．すると，日常的経験と乖離が在って「はて？」となります．

＞次いで，「動き続けるには力が必要」．摩擦のない台車に摩擦のある物体を引きずらせます．一定の速度で引くとき，台車が手から引かれる力と，引きずっている物体から引かれる力とどっちが大きいか．多くの初学者は手が引く力が大きいと思っている．

この部分は良く判らないのですが，「静的な力のへ平衡」と「動的な運動方程式を立てるときの作用反作用」との統一的な理解が得られ難いということならば，理解出来ます．

ただ「多くの初学者は手が引く力が大きいと思っている．」ということは初めてお効きしました．

＞私が強調しているのは，全くの初学者のレベルです．

なお，私が「初学者」と言った場合，高校〜大学で力学を学習始める方々を想定しています．ただし，今から40年ほど前の事になる訳ですが．

＞「力が掛からない限り運動量も変わらないという日常感覚」といいきれるmNejiさんの常識は決して初学者のものではありません．

ああ，そうですね．上の認識が出来たのは，独学で「PSSC物理」を学んだお蔭だろうとおもいます．当時，自分で実験用のツルツルなリンクと，ドライアイスが欲しかったと思いましたが，高校生のころにはアマチュア無線につられていて，力学実験には手が出ませんでした．

でも，アイス・スケートをして「力が掛からない限り運動量も変わらないという日常感覚」は正解だと感じたのも確かです．むしろ，現代では映像資料も，実験素材も豊富に存在しているのですから，通常の教科書なんて捨てて，自分の日常事例として，運動の骨格を学ぶ事は可能だとおもいますが．

＞初歩的な「慣性の法則」の言葉と概念を不要のものと捨て去ることができるのか．私にはどうしてもわかりません．

数年前に，この掲示版に来て以来，「高校の物理」がどう変わったかを知る為に，数種類の教科書を買いましたが，独学派の私は，余程の事がないと眺めるげんきがありません．しかし，その内の一冊，三省堂の本が取り易かったので拝見しましたが，「３章運動の法則」の中に ・１慣性の法則 ・２運動の法則 ・３運動の法則の適用 ・（以下略） となっています．え，「作用反作用の法則」がありません，

探して見ると，「２運動の法則」の中に，【ニュートンの運動の３法則】という小さな項目にプリンキピアの紹介として簡単に触れられているだけです．そこで，死蔵しているプリンキピアの英語訳，「THE PRINCIPIA, Mathematical Principles of Natural Philosophy」を眺めて見ると，「Axioms, or the Lows of Motion 運動の法則または原理」の冒頭に，「Law 1, Law 2, Law 3」が手短に書かれています．

その「Law 1 第一法則」には，「慣性の法則」がどんと書かれているかと思いきや，とても簡素な記述でした．参考までに引用します．

〜〜〜〜〜 <b>Law 1 </b>

Every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by forces impressed.

Projectiles persevere in their motions, except insofar as they are retarded by the resistance of the air and impelled downward by the force of gravity. A spinning hoop ^(d) , which has parts that by their cohesion continually draw one another back from rectilinear motions, does not cease to rotate, except insofar as it retarded by the air. And larger bodies---planets and comets---perserve for a longer time both their progressive and circular motions, which take place in spaces having less resistance.

^(d) spinning hoop: a top or some kind of spinner.

〜〜〜〜〜

勿論，それに続く本文を読んでいませんが，「ヴェクタとしての力」などから始まり，「幾何学的な微分算法」，「天体の運行」，「光学」，「天文学」などの分厚い説明が在る様です．

私は，ニュートンさんの本には「慣性」という語彙が満載だろうと思っていたのですが，驚いています．

やはり「慣性の法則」を前面にして，初心者に力学を教えるスタイルは見直してもいいのではないかと思うものです．

Yokkun さんのレス (2009/06/10(Wed) 15:38)

>すると，日常的経験と乖離が在って「はて？」となります．

そうです．ですから，空気抵抗にその正体を見定めながら，まずはその影響をとりのぞいてみよう・・・という方法論になります．

>え，「作用反作用の法則」がありません，

運動の法則にようやく出てきたのでは遅いんです．力の発見と重要な関わりを持つのですから，当然静力学＝力のつりあいの部分に載ってるはずですね．

>ニュートンさんの本には「慣性」という語彙が満載だろうと思っていたのですが・・・

何度もいっていますが，語彙の問題ではありません．内容の問題です． まさかプリンキピアを持ち出されるとは思いませんでしたが．＾＾；

>「慣性の法則」を前面にして，初心者に力学を教えるスタイルは・・・

「前面にして」との解釈はmNejiさんの勝手な解釈です．私は「慣性の法則」および慣性の大いさとしての質量の意味の拡大が，初学者が第2法則を学ぶ上で大切ですよといっているのです．教科書のお題目が問題ではないんです．力の発見や静力学から運動力学へと歩を進めるにあたって，準備されるべき概念ですよといっているのです．実際，力学の教科書のどれをみても「慣性の法則」自体は何ページも割いているものはなく，さらりと流していますよね．今そんなことは関係ない．準備されておくべき概念・法則としてどれだけ重要であるかということです．

乗り越えるべき「常識」としてもうひとつ．これこそは慣性とかかわるものですが，重たいものは動きにくいという正しい法則が，初学者においては日常の重力および摩擦がある中での制約された経験とりくつにとどまっているという点です．重いから摩擦も大きく動きにくいというのは，慣性の概念とは別の問題です．摩擦がなかったり，無重力であっても重いものは動きにくいのだという理解が必要です．そしてさらに強調したいことは，どんな小さな力でもそれがゼロでない限りどんな重いものも動かすことができるということですね．摩擦にだまされている限り，慣性の本質をとらえることができないわけです．

mNeji さんのレス (2009/06/10(Wed) 16:38)

＞そうです．ですから，空気抵抗にその正体を見定めながら，まずはその影響をとりのぞいてみよう・・・という方法論になります．

ですから「ピサの斜塔」を無造作に出すのは反対です．

＞運動の法則にようやく出てきたのでは遅いんです．力の発見と重要な関わりを持つのですから，当然静力学＝力のつりあいの部分に載ってるはずですね

ところが，運動方程式を立てるときに，「作用反作用」を適用できないケースを多々見受けます．すなわち，静力学では作用反作用を使えても，動力学では作用反作用を使えないという深刻な事態になっていると思います．

＞何度もいっていますが，語彙の問題ではありません．内容の問題です．

私も，何度でも申し上げますが「慣性〜〜」という単語を必要以上に用いずに，その示すべき内容を説明するべきだろうと思います．また「慣性」という言葉を使う場合は，相手の力量に応じて使わないと，「慣性」→「慣性力」→「仮想的な力」→「計算上だけの力」といった誤解が発生しやすい事に目を向けるべきです．かれこれ3年間に渡りこの数学掲示版を拝見して来た経験からの帰結です．

＃ 「慣性の法則」を「ニュートンの運動の第一法則」と書くのもいいですね． ＃ 運動方程式を第二法則，作用反作用を第三法則とか． ＃ 自分では，「作用反作用，慣性，運動方程式」の順に覚えていましたが ...．

＞乗り越えるべき「常識」としてもうひとつ．

これこそ，ニュートンの第二法則の解釈問題です．慣性と関わりの有無はべつとしても，多面的に論じるべき課題だと思います． その為に，この数学掲示版があるような気がします．

Yokkun さんのレス (2009/06/10(Wed) 17:31)

>ですから「ピサの斜塔」を無造作に出すのは反対です．

さて，「ピサの斜塔」はいったい誰が持ち出したのか？ Electraさんは，「ピサの斜塔の実験の部分」といっていますが，本来の引用された部分はピサの斜塔の実験のことではなく，一般の自由落下についての内容です． 誰も「「ピサの斜塔」を無造作に出」してなんかいません．それとも，かぎしっぽの該当部分の記述を批判されているのですか？それならば話は別で，私はひとまず聞き流したいと思います．

>運動方程式を立てるときに，「作用反作用」を適用できないケースを多々見受けます．すなわち，静力学では作用反作用を使えても，動力学では作用反作用を使えないという深刻な事態になっていると思います．

同感です．しかし，作用反作用則を動力学で使えない場合の多くは，静力学でも使えないケースが多いと思います．作用反作用則とつりあい関係の混同が，最も多くみられる誤りです．作用反作用をつりあいと勘違いするから，つりあってない動力学では関係ないと思ってしまうのでしょう．これは，最近の「深刻な事態」というより，専門家にさえ昔からよく見られる誤りです．情けない実例がたくさんあります．

>「慣性」→「慣性力」→「仮想的な力」→「計算上だけの力」といった誤解が発生しやすい

これは，一般にいえる傾向なのですか？一般に多いとはとても考えられない連想ゲームです．

>ニュートンの第二法則の解釈問題です．慣性と関わりの有無はべつとしても，多面的に論じるべき課題・・・

うーん．「解釈問題」ですか？おっしゃっていることが飲み込めません．もっと単純な問題で，プリンキピアのLaw1でいわれている通りだと思っています．多面的に論じることはかまいませんが．

大体，問題は収束したと思います．このスレッドでの質疑に関する限り，上のような「慣性」→「慣性力」といった混乱はありえない話です．「慣性」と「慣性力」とは（無関係とはいいませんが）全く別の概念です．「慣性力」を理解している方にとっては，混乱の余地がないと思います．そして，本スレッドでの質疑に関しては，「慣性力」についての議論の必要は全くありませんから，知っている必要もありません．一方，「慣性」自体については，用語としての必要の問題で少しく意見がわかれましたが，溝は深いようです．しかし，概念としての重要性を否定されたわけではないと思いますので，これまでとしましょう．

でも，上の（「慣性」→「慣性力」）ような混乱があり得るという事実は私にとっても大変勉強になりました． 楽しく議論させていただき，ありがとうございました．m(_ _)m