複素関数論について

ぽぽさんの書込 (2009/06/06(Sat) 18:58)

複素関数論を勉強しているのですが，コーシー，リーマンの方程式とかいうのがでてきてそれで，微分可能性を判定するんですが

そのなかでよくわからないワードがでてきました．

「連続な偏導関数」

ある偏導関数が示されて，これは「連続な偏導関数」だから・・・と書いてあるのですがなぜ？？？っていう理由を省いて書いてあるのでよくわかりません．

ある偏導関数が「連続な偏導関数である」ということは一目見てぱっとわかるもんなんですか？

よろしくお願いしますｍ（＝＝）ｍ

や $\exp(-x^2/2)$ が連続であることは分かりますか?また，上の関数を微分してできた関数(導関数) や $-x\exp(-x^2/2)$ が連続であることは分かりますか?

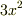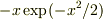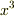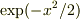つまり， 3x^2 や $-x\exp(-x^2/2)$ は「連続な導関数」であり，言い換えると， x^3 や $\exp(-x^2/2)$ は「連続な導関数」を持ちます．

この概念を常微分から偏微分に拡張しただけです．

# それとも，ある関数が連続かどうかを「一目見てぱっとわかる」方法をお探しですか?

あ，わかりました．

よくわからなくて関数の連続性の定義なんかみてしまって頭がこんがらがってました．

なんだかすっきりしました．ありがとうございました．