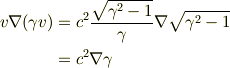宿題の途中の式
宿題の途中の式
ゆい さんの書込 (2009/06/02(Tue) 13:45)
となることを証明したいのですがうまくいきません.ここで 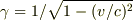 ,
,  は三次元の速度ベクトルです.
公式
は三次元の速度ベクトルです.
公式
 を使って
を使って
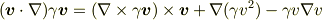
となったんですが, 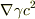 の項が出ません.教えていただけないでしょうか
の項が出ません.教えていただけないでしょうか
Re: 宿題の途中の式
toorisugari no Hiro さんのレス (2009/06/02(Tue) 15:28)
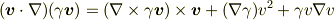
の間違いでは? # 追記 間違っていませんでしたね.
さらに, 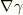 を計算すると,
を計算すると, 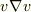 の係数倍であることが分かるので,それを利用して,最後の2項は
の係数倍であることが分かるので,それを利用して,最後の2項は  になります.
になります.
Re: 宿題の途中の式
ゆい さんのレス (2009/06/02(Tue) 15:50)
ありがとうございます.
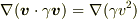 と考えたのですが
と考えたのですが 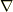 は
は 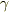 だけでなく
だけでなく  に作用するので括弧の外には出せないと思いました.計算間違いでしょうか
に作用するので括弧の外には出せないと思いました.計算間違いでしょうか
Re: 宿題の途中の式
ゆい さんのレス (2009/06/02(Tue) 16:50)
すいません. 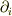 とかで表示するやりかたはまだ勉強してなくてわかりません.
とかで表示するやりかたはまだ勉強してなくてわかりません.
Re: 宿題の途中の式
Yokkun さんのレス (2009/06/02(Tue) 18:02)
ゆいさん,こんばんは.
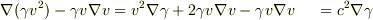
になると思います.
toorisugari no Hiroさん,ひょっとして左辺は 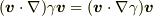 でよいのではないでしょうか?
でよいのではないでしょうか?
Re: 宿題の途中の式
toorisugari no Hiro さんのレス (2009/06/02(Tue) 19:30)
元の式はあってました.というか,どれも一緒ですね.
> toorisugari no Hiroさん,ひょっとして左辺は |3aaf4d746a65051a8573c25da093c4f2| でよいのではないでしょうか?
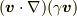 としないとでないと思いますが.たぶん.
としないとでないと思いますが.たぶん.
Re: 宿題の途中の式
Yokkun さんのレス (2009/06/03(Wed) 08:45)
toorisugari no Hiroさん,No.23994を追跡して確認できました.混乱させてごめんなさい.
ゆいさん, 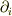 等の記法はとても便利なのでこの際覚えられるとよいと思います.理解すべきルールは2つ.まず,定義は
等の記法はとても便利なのでこの際覚えられるとよいと思います.理解すべきルールは2つ.まず,定義は
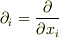
で,添字 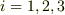 に対して
に対して 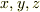 を割り当てます.微分演算子
を割り当てます.微分演算子 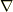 をちょうどベクトルと同じにあつかって,添字でその成分を表すわけです.
をちょうどベクトルと同じにあつかって,添字でその成分を表すわけです.
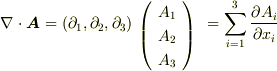
という具合. もう1つは,アインシュタインの和の規約.たとえば,内積を
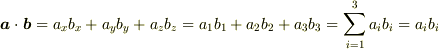
と略記します.同じ添字がひとつの項の中に現れたら和をとるというルールです.すると,
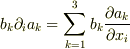
等ということになります.慣れるのにちょっと時間がかかるかもしれませんが,記述がすっきり簡略化されてとても便利ですよ.
Re: 宿題の途中の式
toorisugari no Hiro さんのレス (2009/06/03(Wed) 10:09)
Yokkunさんfollowありがとうございます.
> 混乱させてごめんなさい.
いえいえ,こちらも計算間違いしていたので,お気になさらずに.
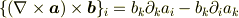
を自己followしておきます.
ベクトル3重積の公式より
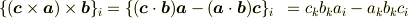
となります. 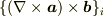 は
は  を
を 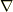 に置き換えればいいのですが,一つ注意点があります.
に置き換えればいいのですが,一つ注意点があります.
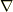 は微分演算子で
は微分演算子で 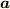 に作用しています.ですから,
に作用しています.ですから, 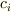 を
を 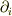 に変えるとき
に変えるとき 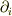 の右に
の右に 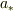 がくるように順番を変えなければいけません.
がくるように順番を変えなければいけません.
よって
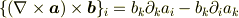
が得られます.
いずれレビチビタの3階完全反対称テンソル
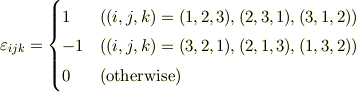
と公式
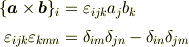
を使って計算する方法も習われると思います.
Re: 宿題の途中の式
ゆい さんのレス (2009/06/03(Wed) 12:46)
toorisugari no Hiroさん,Yokkunさん ありがとうございました.無事導出できました.テンソル表示は今後勉強していきたいと思います.
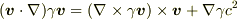
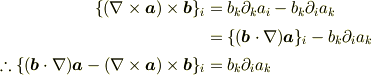
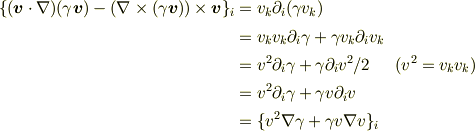
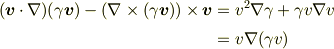
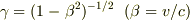 より
より