リサージュ図形と発振回路について

リサージュ図形と発振回路について

はまはま さんの書込 (2009/06/02(Tue) 12:24)

はじめまして．発振回路に関することで質問があります． 発振回路の周波数をオシロスコープにリサージュ図形を表示させて測定するような実験を行いましたが， なぜリサージュ図形を表示させることにより発振周波数が測定できるのでしょうか？ 原理的な質問で申し訳ありませんが，すごい疑問に思うのです． 回答よろしくお願いいたします．

Re: リサージュ図形と発振回路について

mNeji さんのレス (2009/06/02(Tue) 12:35)

どのような実験をされたのかが不明ですが，おそらく，x軸の入力に測定対象の信号を入れ，y軸の入力に周波数を可変できる発信器の信号を入れませんでしたか？

どのような操作をして，どのような結果が出て，判らない点が何処か，をお書きになればと思います．

Re: リサージュ図形と発振回路について

はまはま さんのレス (2009/06/02(Tue) 14:44)

オシロスコープに正弦波発振回路と発振回路実験装置（被測定物）を繋ぎ，コンデンサＣと抵抗Ｒから求めた発振周波数の理論値を元に，周波数を変えていき，リサージュ図形を表示させました． 表示されたときに測定値の周波数の値が出るので，それを記録していきました．

そこでわからないのは，なぜリサージュ図形を表示させることで発振周波数が測定できるのか？というものです．

Re: リサージュ図形と発振回路について

mNeji さんのレス (2009/06/02(Tue) 14:57)

参照用の発信器の周波数を固定しないで，自分で組んだ発進回路の時定数から求めた周波数の近傍を段々とスイープしていき，オシロスコープの表示が単純な波形になる所を探した訳ですよね．

ギターの調弦する場合では，固定した周波数をだす音叉に対して，ギターの弦の張力をスイープしながら周波数の差が単純になる所を探す訳です．

オシロスコープでも，リサージュ波形が単純になれば，両者の周波数が一致したと考えて良いのではないでしょうか．

Re: リサージュ図形と発振回路について

mNeji さんのレス (2009/06/03(Wed) 09:19)

このご質問を見ているうちに，私もリサージュ波形が不思議だったことを思い出しました．

いま，X軸とY軸に同一の角振動数 \omega の信号が振幅A,Bで入っているとします．ただ，Y軸には位相の遅れ，位相角 \delta があるとします．

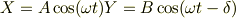
X=A\cos(\omega t)Y=B\cos(\omega t -\delta)

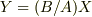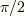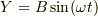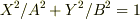位相角が特別な場合は，リサージュ波形は簡単になります．特に位相角がゼロなら， Y=(B/A)X と直線ですし，位相角が \pi/2 なら Y=B\sin(\omega t) となるので楕円， X^2/A^2 + Y^2/B^2 =1 となります．

この途中の位相角の場合を理解する為に，新たな変数を導入します；

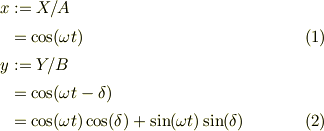
x &:= X/A\\&= \cos(\omega t) &\ (1)\\y &:= Y/B\\&= \cos(\omega t -\delta)\\&=\cos(\omega t)\cos(\delta) + \sin(\omega t)\sin(\delta) &\ (2)

位相角が直角の場合では楕円になる事から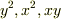， y^2, x^2, xy などからリサージュ波形が出て来ると思われますので書き出します；

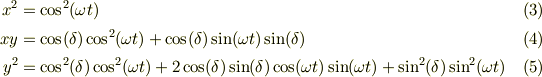
x^2 &= \cos^2(\omega t) &\ (3)\\xy &= \cos(\delta)\cos^2(\omega t) +\cos(\delta)\sin(\omega t)\sin(\delta) &\ (4)\\y^2 &= \cos^2(\delta)\cos^2(\omega t)+2\cos(\delta)\sin(\delta)\cos(\omega t)\sin(\omega t) +\sin^2(\delta)\sin^2(\omega t) &\ (5)

これらをじっと見つめていると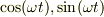， \cos(\omega t), \sin(\omega t) の項を消去できるとおもいませんか？具体的にやって見ましょう；

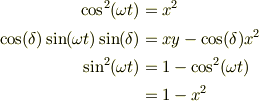
\cos^2(\omega t) &= x^2\\\cos(\delta)\sin(\omega t)\sin(\delta) &= xy -\cos(\delta)x^2 \\\sin^2 (\omega t) &= 1- \cos^2(\omega t)\\&= 1-x^2

ですから，

y^2 &= \cos^2(\delta)\cos^2(\omega t)+2\cos(\delta)\sin(\delta)\cos(\omega t)\sin(\omega t) +\sin^2(\delta)\sin^2(\omega t)\\&= \cos^2(\delta)x^2 +2\sin(\delta)[xy-\cos(\delta)x^2] +\sin^2(\delta)(1-x^2)\\&= [\cos^2(\delta)-2\sin(\delta)cos(\delta)-\sin^2(\delta)]x^2 +2\sin(\delta)xy +\sin^2(\delta)

整理すると，リサージュ軌道の関数を得る事が出来ます；

y^2+[\sin^2(\delta)+2\sin(\delta)cos(\delta)-\cos^2(\delta)]x^2-\sin(\delta)xy & =\sin^2(\delta) &\ (6)