慣性力 エレベータ
慣性力 エレベータ
under さんの書込 (2009/05/26(Tue) 21:49)
一定の加速度aで垂直に下降するエレベータの中で，床からhの高さの ところから水平に速さvで投げたボールは，エレベータの中では， 水平方向にどれだけ進んで床に落ちるか．
と言う問題なのですが，
ボールの運動方程式は鉛直上向きにｙ軸，水平方向にｘ軸をとると， m(d^2x/dt^2)=0・・・ア m(d^2y/dt^2)=ma-mg・・・イ 初期条件はt=0で x=0,y=0,dx/dt=v,dy/dt=0 運動方程式より アよりd^2x/dt^2=0 これと初期条件より2回積分するとx=vt イよりd^2y/dt^2=a-g これと初期条件より2回積分するとy=(1/2)(a-g)t^2 で水平方向にどれだけ進んでというのは このyの式でいいんでしょうか？ また，この初期条件でt=0のときy=0というのがいまいち よく分からないので教えてください．(yは縦軸なのになんでhにならないのかな？っていうことです．)
Re: 慣性力 エレベータ
Yokkun さんのレス (2009/05/27(Wed) 00:47)
>水平方向にどれだけ進んでというのは このyの式でいいんでしょうか？
水平方向にx軸をとったはずですよね． 落下時間tを求めなければいけません．
>初期条件でt=0のときy=0というのがいまいち よく分からないので教えてください．
座標軸のとりかたは指定されていませんから原点をどこに置くかは全くの自由です．単に初期位置を原点にとっただけですね？この解答例のとりかたでは，床がy=-hになるわけです．
Re: 慣性力 エレベータ
under さんのレス (2009/05/27(Wed) 06:24)
y=(1/2)(a-g)t^2より y=-hを代入 t^2=(-2h)/(a-g) よってt=√{(-2h)/(a-g)} x=v√{(-2h)/(a-g)} これであってますか？
Re: 慣性力 エレベータ
Yokkun さんのレス (2009/05/27(Wed) 12:23)
あっていると思います．
（天井にでなく）床に落ちることが前提ですから，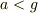 
なのですね．根号の中は分母分子とも符号を反転するのがすっきりするでしょう．
