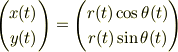2次元極座標の速度
2次元極座標の速度
under さんの書込 (2009/05/24(Sun) 15:56)
2次元平面内を運動する物体がある．この物体の運動をデカルト座標を用いて表すと，その速度は v(t)={dx(t)/dt}i+{dy(t)/dt}j 但しi,jはx軸，y軸の単位ベクトル． と表せる．同様のことを2次元極座標を使って表すと， 動径方向の単位ベクトルをer(t)，角度方向の単位ベクトルをeθ(t)として， v(t)={dr(t)/dt}er(t)+r(t){dθ(t)/dt}eθ(t) と書けることを示せ．但し，r(t)=√{x(t)^2+y(t)^2}とし，角度θ(t)はx軸から 測った角度とする．（ x(t)=r(t)cosθ(t)，y(t)=r(t)sinθ(t) )
と言う問題なのですが，わかりません．どうすればいいでしょうか．
Re: 2次元極座標の速度
under さんのレス (2009/05/24(Sun) 18:45)
x(t)/dt=vx(t)=v(t)cosθ(t)-r(t)sinθ(t) y(t)/dt=vy(t)=v(t)sinθ(t)+r(t)cosθ(t) でいいでしょうか？
ここからどうすればいいですか？
Re: 2次元極座標の速度
under さんのレス (2009/05/25(Mon) 05:20)
x(t)/dt=vx(t)={r(t)/dt}cosθ(t)-r(t)sinθ(t) y(t)/dt=vy(t)={r(t)/dt}sinθ(t)+r(t)cosθ(t)
でしょうか？
Re: 2次元極座標の速度
toorisugari no Hiro さんのレス (2009/05/25(Mon) 11:44)
は
の関数です．
またr(t)/dt等の記述は意味不明です．微分ならdr/dt等と書くべきですね．
微分をきちんと勉強された方がよいようです．
Re: 2次元極座標の速度
under さんのレス (2009/05/25(Mon) 18:06)
まちがえました． x(t)/dt={dr(t)/dt}cosθ(t)-r(t){dθ(t)/dt}sinθ(t) y(t)/dt={dr(t)/dt}sinθ(t)+r(t){dθ(t)/dt}cosθ(t) でしょうか？
Re: 2次元極座標の速度
toorisugari no Hiro さんのレス (2009/05/25(Mon) 19:08)
x(t)/dtが相変わらず変ですね．
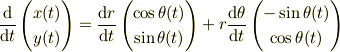
ここで，
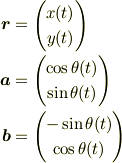
と置くと，
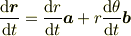
と書けます．
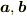のそれぞれの大きさはいくらですか?間の角度はいくらですか?
Re: 2次元極座標の速度
under さんのレス (2009/05/25(Mon) 19:51)
あーすいません．まちがえました． dx(t)/dt={dr(t)/dt}cosθ(t)-r(t){dθ(t)/dt}sinθ(t) dy(t)/dt={dr(t)/dt}sinθ(t)+r(t){dθ(t)/dt}cosθ(t) えーっとa,bの大きさ |a|=√{(cosθ(t))^2+(sinθ(t))^2} |b|=√{(-sinθ(t))^2+(cosθ(t))^2} ですかね？角度はわかりません．
Re: 2次元極座標の速度
Yokkun さんのレス (2009/05/25(Mon) 22:35)
underさん，大きさ最後まで計算しましょう． 角度は，ベクトルの内積をとってみたら？
Re: 2次元極座標の速度
under さんのレス (2009/05/26(Tue) 16:42)
|a|=√{(cosθ(t))^2+(sinθ(t))^2}=1 |b|=√{(-sinθ(t))^2+(cosθ(t))^2}=1 a・b=-sinθcosθ+sinθcosθ=|a||b|cosθ cosθ=0 θ=±π/2 でしょうか？
Re: 2次元極座標の速度
toorisugari no Hiro さんのレス (2009/05/27(Wed) 09:40)
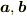>> のそれぞれの大きさはいくらですか?間の角度はいくらですか?
> |a|=√{(cosθ(t))^2+(sinθ(t))^2}=1
> |b|=√{(-sinθ(t))^2+(cosθ(t))^2}=1
> θ=±π/2
> でしょうか？
はい．つまり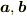， は互いに直交する単位ベクトルです．
さらに
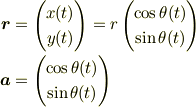
より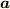 
と 
は平行ですから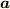， は動径方向を向いた単位ベクトルです．つまり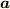， は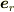 
と書くのがふさわしいです．
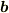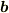は動径方向に垂直で反時計回り(絵を描いて確かめてください)，つまり， の増える向き，を向いた単位ベクトルですから は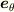 
と書くのがふさわしいです．
以上より
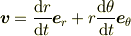
ただし，(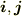 
を使いましょうか)
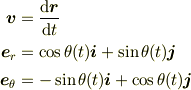
となります．
