一次元箱形ポテンシャル
一次元箱形ポテンシャル
えり さんの書込 (2009/05/24(Sun) 15:34)
以下の問題を解いているのですが,どんどん複雑になっていってしまったので,助言を頂ければと思い投稿させていただきました.
「次のようなポテンシャルの中での質量Mの粒子を考える. V(x)=0(0<x<L),V(x)=V_0>0(x<0,L<x) この束縛状態について次の問いに答えなさい.
…境界条件を課してハミルト二アンの固有関数と固有値を決めなさい.」
という問題で,解いてみました.
シュレーディンガー方程式の一般解は, 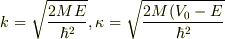 とすると,
とすると,
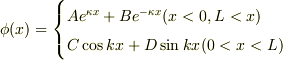
となる.境界条件より,
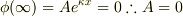
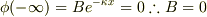
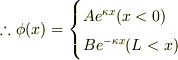
また,x=0,Lでの接続条件より,
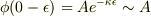
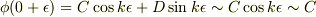
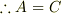 …
となったのですが,x<0,L<xの領域での一般解は一つにまとめられるのでしょうか?それともA,B,C,Dなど4文字を用いて,2式に分けて表記しなければいけないのでしょうか?また,接続条件も用いるとA=Cのようになってしまい,式の整理に困っています.
上記のような解き方で良いのか不安になっているため,助言を頂きたいと思っています.よろしくお願いいたします.
…
となったのですが,x<0,L<xの領域での一般解は一つにまとめられるのでしょうか?それともA,B,C,Dなど4文字を用いて,2式に分けて表記しなければいけないのでしょうか?また,接続条件も用いるとA=Cのようになってしまい,式の整理に困っています.
上記のような解き方で良いのか不安になっているため,助言を頂きたいと思っています.よろしくお願いいたします.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/24(Sun) 16:16)
これから出かけるので,簡単にコメントします.
この場合,領域は3つに分かれませんか;(x<0, 0<=x<=L, L<x).すると波動関数の定数は,計6個になりますね.
波動関数には, ・x=0,x=Lで,波動関数が一致,波動関数の導関数が一致, ・左右の無限遠での波動関数がゼロ. の計6本の条件が出来るのでは?
Re: 一次元箱形ポテンシャル
えり さんのレス (2009/05/25(Mon) 00:05)
やはり定数は6つになるのですね.外側は同じポテンシャルなのでひょっとしたら1つの式にまとめられるのかと思ってしまいました.
確かに,未知数が6つにもなってしまいますが同様に条件も6つ出てくるので,普通に解けそうですね… 簡単な質問をしてしまい,すみませんでした. また解いてみます.ありがとうございました.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/25(Mon) 02:00)
元に戻ってしまうようですが;
>…境界条件を課してハミルト二アンの固有関数と固有値を決めなさい.」
には,釈然としない感じが残ります.宜しければ,解いた結果をお示し下さいませんか?
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/26(Tue) 12:57)
自己コメントです.
>釈然としない感じが残ります.
ゼロ解でない為の条件から,固有値が出て来るみたいですね.とんだコメントを付けてしまって,申し訳在りませんでした.
Re: 一次元箱形ポテンシャル
えり さんのレス (2009/05/26(Tue) 13:02)
すみません,実はまだ解けていないのですが,未知数を6文字において解いたものの途中経過を示してみようと思います.
シュレーディンガー方程式は
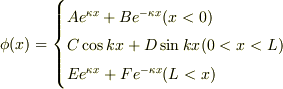 境界条件より
境界条件より
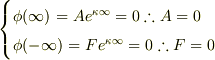
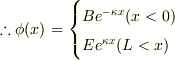
 での接続条件より,
での接続条件より,
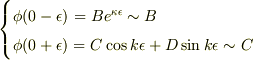
 …(1)
…(1)
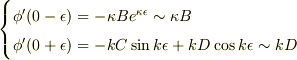
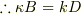 …(2)
…(2)
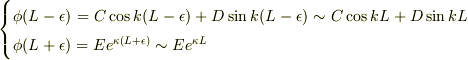
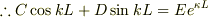 …(3)
…(3)
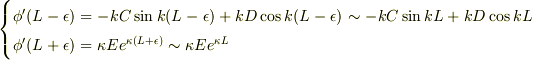
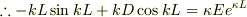 …(4)
…(4)
(1),(2)より, 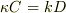 …(5)
…(5)
(3)×  -(4)より,
-(4)より,
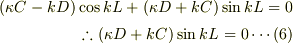 最後の式は(5)を用いた.
最後の式は(5)を用いた.
と,ここまで解いたのですが,おそらく後は(6)式と, 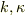 の定義式とを連立して,kとκを求め,エネルギー固有値を求めるのだと思います.
ここで,(6)式ではまだ任意定数が残っていますが,この定数は残さないほうがいいのでしょうか…なんとなく(6)式がきれいな形なので,このままでもいいかなと思ってしまうのすが,それでは後々が大変になるのでしょうか…
の定義式とを連立して,kとκを求め,エネルギー固有値を求めるのだと思います.
ここで,(6)式ではまだ任意定数が残っていますが,この定数は残さないほうがいいのでしょうか…なんとなく(6)式がきれいな形なので,このままでもいいかなと思ってしまうのすが,それでは後々が大変になるのでしょうか…
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/26(Tue) 13:25)
私も,途中まででサボっています.
自分の場合,中間部分を 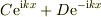 とし,実数
とし,実数  とすると,rの2次方程式に,
とすると,rの2次方程式に, 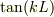 が入って来る様です.
が入って来る様です.
何れにしても,C,Dの連立方程式M*(C,D)=(0,0)で,非零の解の条件,det M =0から決めるのでしょうね.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/28(Thu) 11:33)
---xxx--- 勘違いでコメントしてしまいましたが,これほど計算が複雑になるとは思わず,少々持て余し気味です(笑).そこで,途中までですが,流れを追う一助になるかと思い,計算ノートを書いて見ます.当然,間違いも在ると思うので,ご参考までです.
えりさんの No.23877 に対応しますが,係数は自分のノートに準拠したので,整合性はありません.
波動関数は,左・中央・右と3つに分かれます.左右の遠方で収束するのを考慮して;
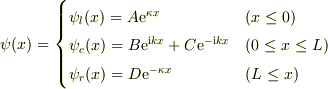
ここで波数;
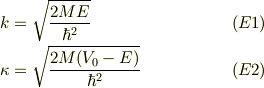
領域の接点での波動関数と導関数の連続性が成り立つ;
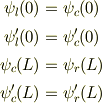
定数  に付いて書き下せば,
に付いて書き下せば,

(1),(2)からAを消去し,(3),(4)からDを消去すると,B,Cについての連立方程式を得る;
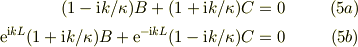
これが(B,C)のゼロ解でない解を持つには,次の固有値方程式が必要となる;
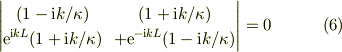
ここで表記の簡単の為に,実変数R;
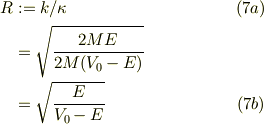
として,式(6)を書き下すと,
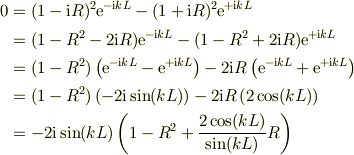
従って,Rの固有値は,2次方程式の解.

係数と根の関係から,  を得るが,さらに三角関数の半角の公式を用いて;
を得るが,さらに三角関数の半角の公式を用いて;
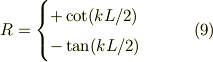
式(9)と式(7b)から波数kが決まると言う感じでしょうかね.
〜〜〜〜〜〜〜 No.24103の式((13a);
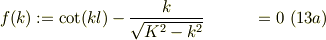
をニュートン法ではなくて,テイラー展開を用いて解く事を考える.ここで,

#テイラー展開では,微分項の独立変数の値が一定であるのがメリットだが,せいぜい2次微分まででないと,実用的でないだろう.
変数を新たに, 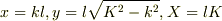 とすると,
とすると,
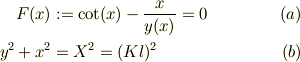
この方程式のゼロ近似解として, 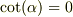 を採用すると,初項
を採用すると,初項 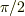 ,ゼロ近似解は公差
,ゼロ近似解は公差  の等差数列となる;
の等差数列となる;
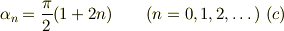
式(a)のテイラー展開は;
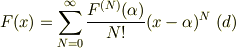
この関数では 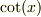 の展開が複雑になる.
の展開が複雑になる.
いっその事,  として,
として,
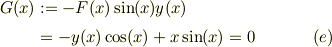
を考えた方が楽かも.
式(b)より,

式(e),(f2),(f3)より
![G(x) &= -X[\sin(\theta)\cos(x) -\cos(\theta)\sin(x)] \\&= X\sin(x - \theta) &=0 &\ (e')](http://hooktail.maxwell.jp/bbslog/d06e4b29661fa1bdd9d2f136d2892807.png)
この場合,式(f2)より,逆に解いたり,xで微分したりして
![\theta(x) &= \text{arccos}(x/X) &\ (g1)\\1 &= -X\sin(\theta)\frac{\mathrm{d}\theta}{\mathrm{d} x}\\&= -X\sin(\theta)\dot \theta &\ (g2)\\\dot \theta &= \frac{-1}{X\sin(\theta)} &\ (g3)\\\ddot \theta &= \frac{-1}{X}(-[\sin(\theta)]^{-2})\dot \theta\\&= \frac{1}{X\sin^2(\theta)}\frac{-1}{X\sin(\theta)}\\&= \frac{-1}{X^2\sin^3(\theta)} &\ (g4)](http://hooktail.maxwell.jp/bbslog/66e41da106f07bee0277dc0d8dee4456.png)
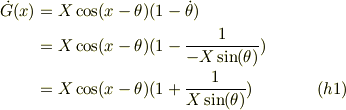
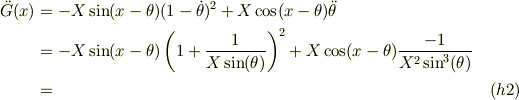
---XXX---

Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/30(Sat) 00:08)
まだどこかが変な感じですが,問題点が判っていません.
検算の一つとして,エナジ 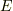 に比べて,ポテンシャル障壁
に比べて,ポテンシャル障壁  が十分に大きな極限であるとして,その振る舞いを考えて見ました.
が十分に大きな極限であるとして,その振る舞いを考えて見ました.
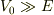 なので,
なので, 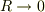 となるので,
となるので,
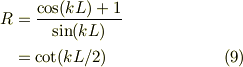
から,すなわち, 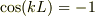 の条件として,
の条件として,

となってしまいます.
〜〜〜〜
と書きましたが, 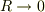 の極限では,正の解だけではなくて,負の解,
の極限では,正の解だけではなくて,負の解,
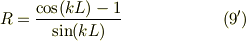
も考える必要があるようです.すなわち  から,
から,

従って,通常の波数の量子化と同様に,

が出てくようです.
従って,有限の  では,式(9)からの固有値についての論議を展開するので良い可能性が高まりました.
では,式(9)からの固有値についての論議を展開するので良い可能性が高まりました.
Re: 一次元箱形ポテンシャル
ヒノッキー さんのレス (2009/05/30(Sat) 11:16)
こんにちは. ・・・参考までにですが,類似問題とその解説が書いてある本があったので, のせておきます.
共立出版「詳解量子力学演習」P44
・・・範囲が0<x<L,でなく,-a<x<aになってたり もとめるものが,束縛状態のエネルギーのみだったりしますが, 参考にはなるかと思います.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/30(Sat) 14:37)
ヒノッキーさん,情報感謝します.
>共立出版「詳解量子力学演習」
というのは,「マギアリ・コンスタンチネスキュ著波田野彰・訳」という図書ではありませんよね?これなら,区図書館にあるのですが.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/30(Sat) 19:09)
計算ノートのさらに予備ノート 〜〜〜〜〜〜〜
エナジ固有値を考えます.それには,
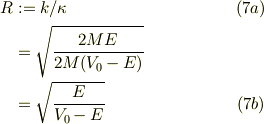
と
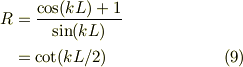
と
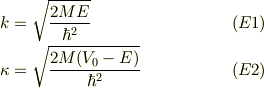
とを連立して解くだけです.
でも,実際にはどうすれば良いかです.余接関数(cot(x))は,正の領域だけに着目すれば,連続的に単純減少し,かつ,周期性があることが味噌だとおもいます.
式(E2)を操作し易くする為に,次の常数を導入する;

すると,式(E2)より
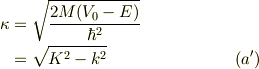
式(7b),(9)を連立して解く事は,次の関数 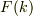 の根「
の根「 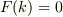 」を得る事である;
」を得る事である;

残念な事に,こんな面倒な式を直接に解けないから,逐次近似法が必要となる.例えば, ・ニュートン法, http://ja.wikipedia.org/wiki/%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E6%B3%95 を用いるのも一法である.
式(b) は,ポテンシャル障壁が十分に大きいと,  だし,自由運動の幅
だし,自由運動の幅 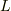 が十分に小さければ,交点は小さな
が十分に小さければ,交点は小さな 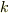 に留まる事ができる.
に留まる事ができる.
ニュートン法を用いる為に,導関数を求めておく;
![F(k) &= \cot(kL/2) - k(K^2 -k^2)^{-1/2}\\F'(k) &= (L/2)\frac{-1}{\sin^2(kL/2)} -(K^2 -k^2)^{-1/2} -k\frac{-1}{2}(K^2 -k^2)^{-3/2}(-2k)\\&= \frac{-L}{2\sin^2(kL/2)}-(K^2 -k^2)^{-1/2}\left[ 1-\frac{k^2}{(K^2-k^2)} \right]\\&= \frac{-L}{2\sin^2(kL/2)}-(K^2 -k^2)^{-1/2}\frac{K^2-2k^2}{K^2-k^2} &\ (c)](http://hooktail.maxwell.jp/bbslog/417e73879d4d1e569f05d3a98470b007.png)
実際に,kの第ゼロ近似として 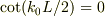 を採れば良いので;
を採れば良いので;
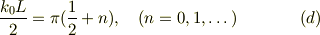
kの第1近似値は,ニュートン法に依って,
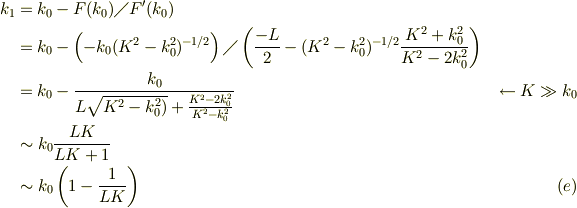
● 奇関数の場合:
〜〜〜〜 No.23907の後半の固有値方程式

を同様に解く. 〜〜〜〜
今度は,次の方程式を解く事だ;
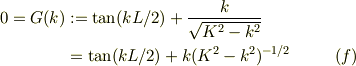
第ゼロ近似は 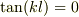 の根として良いが,
の根として良いが, 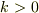 なので,
なので,
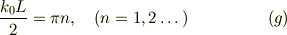
ニュートン法を用いる為に,導関数を求めておく;
![G(k) &= \tan(kL/2) + k(K^2 -k^2)^{-1/2}\\ G'(k) &= (L/2)\frac{+1}{\cos^2(kL/2)} +(K^2 -k^2)^{-1/2} +k\frac{-1}{2}(K^2 -k^2)^{-3/2}(-2k)\\ &= \frac{L}{2\cos^2(kL/2)}+(K^2 -k^2)^{-1/2}\left[ 1+\frac{k^2}{(K^2-k^2)} \right]\\ &= \frac{L}{2\cos^2(kL/2)}+(K^2 -k^2)^{-1/2}\frac{K^2-2k^2}{K^2-k^2} &\ (h)](http://hooktail.maxwell.jp/bbslog/34b857a0234f66fd8cc891ce4b2dd939.png)
kの第1近似値は,ニュートン法に依って,
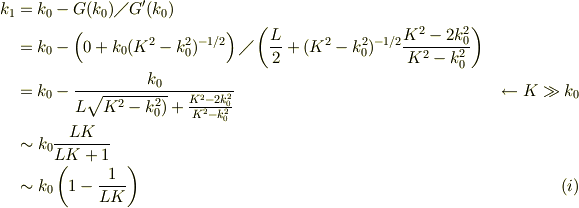
kの第1近似値の第ゼロ近似値への補正は,偶関数の場合の式(e)と同様となる.
〜〜〜〜 計算メモ:三角関数の微分が苦手なので,自己アンチョコ
![\mathrm{e}^{\mathrm{i}x} &= \cos(x) +\mathrm{i}\sin(x) &\ (m1)\\\frac{\mathrm{d}}{\mathrm{d}x}\mathrm{e}^{\mathrm{i}x} &=\mathrm{i}\mathrm{e}^{\mathrm{i}x} = -\sin(x) +\mathrm{i}\cos(x)\\&= \frac{\mathrm{d}}{\mathrm{d}x}\cos(x) +\mathrm{i}\frac{\mathrm{d}}{\mathrm{d}x}\sin(x)\\\frac{\mathrm{d}\cos(x)}{\mathrm{d}x} &= -\sin(x) &\ (m2)\\\frac{\mathrm{d}\sin(x)}{\mathrm{d}x} &= \cos(x) &\ (m3)\\\frac{\mathrm{d}}{\mathrm{d}x}\tan(x) &= \frac{\mathrm{d}}{\mathrm{d}x}\sin(x)\cos^{-1}(x)\\&= \frac{\mathrm{d}\sin(x)}{\mathrm{d}x}\cos^{-1}(x)+\sin(x)[-\cos^{-2}(x)]\frac{\mathrm{d}\cos(x)}{\mathrm{d}x}\\&= \frac{1}{\cos^2(x)} &\ (m4)\\\cot(x) &= \tan^{-1}(x)\\\frac{\mathrm{d}}{\mathrm{d}x}\cot(x) &= -\tan^{-2}\frac{\mathrm{d}}{\mathrm{d}x}\tan(x)\\&= \frac{-\cos^2(x)}{\sin^2(x)}\frac{1}{\cos^2(x)}\\&=\frac{-1}{\sin^2(x)} &\ (m5)](http://hooktail.maxwell.jp/bbslog/60c790d3e0829e830b4aa1cc478d7779.png)
〜〜〜〜
Re: 一次元箱形ポテンシャル
ヒノッキー さんのレス (2009/05/31(Sun) 09:58)
>「マギアリ・コンスタンチネスキュ著波田野彰・訳」という図書ではありませ んよね?
「後藤憲一他編」(西山敏之,望月和子など6人での共編) となっている本です.いろいろな問題とその解説がやまほど載ってます. ・・・ただ,今回の問題そのままは出ていません.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/31(Sun) 10:07)
>「後藤憲一他編」(西山敏之,望月和子など6人での共編) >となっている本です.いろいろな問題とその解説がやまほど載ってます.
あ,判りました; ・ http://www.amazon.co.jp/exec/obidos/ASIN/4320031717 でしょうか.
>・・・ただ,今回の問題そのままは出ていません.
この問題は,物理としてよりも,化学や素子開発でのモデルとして観ると興味深いように思います.時間が掛かっても,正しく解いてみようかと....
Re: 一次元箱形ポテンシャル
ヒノッキー さんのレス (2009/05/31(Sun) 10:25)
はいその本です. ただ,内容が複雑で僕には解説はムリです.
強引にL/2だけ移動させてから計算すれば, この本での計算を利用できるかと思います.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/05/31(Sun) 10:36)
>強引にL/2だけ移動させてから計算すれば,
私も[-L/2,L/2]の範囲を採る方が,係数の対称性が高くなるので検算が楽かなあと思ったりしました.でも,一度解いてしまえば,座標原点の取り方には依存しないで,同じ結果が得られる筈ですね.
>この本での計算を利用できるかと思います.
その意味でも,最後には一度拝見したいものです.因に,区図書館の検索で「後藤憲一」を拝見すると,かなりの図書がありましたが「量子力学演習」は在りませんでした.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/02(Tue) 11:38)
遅くなりましたが,No.23932に「計算ノートのさらに予備ノート」に,波数kの第1近似を求める流れを示しました.一応,不自然な感じは無いと思います.でも,細かな計算まで正しいかは未定ですが....
もし正解をご存知でしたら,教えて下さい.
Re: 一次元箱形ポテンシャル
ヒノッキー さんのレス (2009/06/02(Tue) 15:57)
お疲れ様です.ニュートン法まで出てくるとは・・・. 勉強不足で,理解するのにかなりの時間を要しそうです・・・.
とりあえず,量子力学演習で出ている束縛エネルギーの答えだけ
載せておきます.
範囲は,
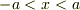 であることに注意してください.
であることに注意してください.
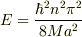
この本は大学構内の本屋に行けば,あると思います.
Re: 一次元箱形ポテンシャル
ヒノッキー さんのレス (2009/06/03(Wed) 00:17)
すみません,そうでした.正しくは,以下のようです.
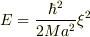
 の定義ですが,この表し方がよくわからないので,
ここは本を見てもらうしかないです・・・.
の定義ですが,この表し方がよくわからないので,
ここは本を見てもらうしかないです・・・.
とりあえず,
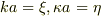 としたとき,
としたとき,
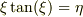 または,
または,
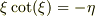 と,
と,
 を用いてグラフを書いたときの交点の
を用いてグラフを書いたときの交点の  の値と
するようです.交点と書いてあるだけで,値はもとめていません.
分かりづらくて申し訳ないです.
の値と
するようです.交点と書いてあるだけで,値はもとめていません.
分かりづらくて申し訳ないです.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/03(Wed) 01:41)
>を用いてグラフを書いたときの交点の  の値と
の値と
おお,素晴らしい情報,有り難うございます.何となく判る様な気がします.少なくとも,固有値方程式を解いていそうです.ただ,
> 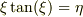 >または,
>
>または,
> 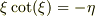 と2本在る様ですね.
と2本在る様ですね.
私の場合は,Rの解を1本に落としているのですが,2本にするべきか考慮中です.
また,座標の取り方は関係ない筈と思うのですが,一度検討してみます.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/03(Wed) 20:25)
皆さん,
どうも「原理的に変な計算をしている」と感じました.そこで,一次元束縛状態の関連でウェブを調べていた所,次の資料; ・ http://physics.s.chiba-u.ac.jp/~kurasawa/qm_a.pdf が解り易く解説しているもようです.
束縛系では,指数関数系の  は一次独立でない上,ポテンシャルが原点について対称ならばは導関数のパリティ保存も要請されるので,正弦関数
は一次独立でない上,ポテンシャルが原点について対称ならばは導関数のパリティ保存も要請されるので,正弦関数 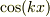 もしくは余弦関数
もしくは余弦関数 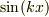 が別々に解となることを知りました.従って,当初のご質問の設定には,ドンピシャリの条件ですね.
が別々に解となることを知りました.従って,当初のご質問の設定には,ドンピシャリの条件ですね.
#束縛状態である事をいい加減にしていた罰ですね. #パリティ保存を指数関数系に適用しても上手く結果を引き出せないのには驚きました. #このpdfの解説はとてもスマートで驚きました.「一様重力での束縛状態」なぞでてきて....こんな解説を見たら量子力学もちょっと魅力的ですね.
また,今回の束縛系の説明は上のpdfに説明されていたと思ったら,勘違いのようです.
ちょっと頭をリラックスしてから,見直してみます.
Re: 一次元箱形ポテンシャル
通りすがりのものです さんのレス (2009/06/04(Thu) 07:37)
はじめまして.
一次元の井戸型ポテンシャルの問題ですね. この問題は有限な井戸の高さの問題ですから,図を描いて求める問題です. (ヒノッキーさんがヒントを与えて下さっている通り) ここの式を詳しくは見ておりませんが,波動関数が無限遠でゼロになる境界条件を見落とされているように思います.
一般に,井戸の高さを無限大にした問題の方が解きやすいです. なお,有限の井戸の高さを無限大する極限をとると,無限大の高さの井戸型ポテンシャルの問題と同じになります.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/04(Thu) 08:33)
通りすがりのものですさん,ご意見有り難うございます.
まさに,一次元の井戸型ポテンシャルの問題です.こんな問題を自分で解こうなんて無謀な事に手を付けてしまい反省しています.
ただご指摘の「波動関数が無限遠でゼロになる境界条件」は適切に入れたとおもいます.
今回の計算で問題だった点は;
- 内部の部分で進行波型解
 を一次独立として扱った.
を一次独立として扱った. - 座標を,内部領域として,
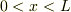 として扱った.その為に,パリティ保存条件を取り込めなかった.
として扱った.その為に,パリティ保存条件を取り込めなかった.
だと思われます.
(1)については,自分の予測では,進行波解を用いていても,正しい固有条件を適用した結果,三角関数解に移行する筈だと推定していたのですが,そうなりませんでした.その上,ゼロ時近似のkLが奇数毎にしか出ませんでした.
そこで,前回引用したpdfを勉強させて戴いたところ,今更ながらに(2),いいかえれば,パリティが束縛解の良い量子数になっていることを気づいた訳です.
その上,束縛条件でのパリティ保存と三角関数解との関係が,これほど密接した関係だと言う認識がありませんでした.昨晩は,これについて指運動をして見ましたが...,座標反転性を進行波型解にいくら適応しても何も出てこない事を知り,驚愕している所です.
>この問題は有限な井戸の高さの問題ですから,図を描いて求める問題です.
そうですね.流石にこの問題と取り組んでいたら,大昔の記憶がほのかに浮かんで来て,図が出て来た記憶はあります.でも問題に,
>境界条件を課してハミルト二アンの固有関数と固有値を決めなさい.
と明示されているので,図に依らない近似解をだそうとトライしてみました.少なくともゼロ近似,1次近似までは出せた様に思います.すこし強引にすれば,2次近似まではだせるかも知れません.でも,そこまでするなら数値計算をしたほうが速いでしょうね.
>一般に,井戸の高さを無限大にした問題の方が解きやすいです. >有限の井戸の高さを無限大する極限をとると,無限大の高さの井戸型ポテンシャルの問題同じになります.
御意.
でもこうしてこの問題にトライしていると,半導体工学が進歩して,いうならば人工分子といっていいような素材開発がされている現代では,このような「有限量子系」のモデル計算としての今回の問題は意外と良いものだなあと感じました.
ただどうせなら,遠方で自由空間,内部領域で負のポテンシャルの方が,よりイメージし易いと思ったのですが,それは先のpdfに解説がありました(笑).
Re: 一次元箱形ポテンシャル
通りすがりのものです さんのレス (2009/06/04(Thu) 11:00)
mNejiさん
> ただご指摘の「波動関数が無限遠でゼロになる境界条件」は適切に入れたとおもいます.
私の方こそ見落としておりました.大変失礼いたしました. (疲れ目でスクロールして見ていたので,まったく気づかなかったようです)
微分方程式の解で,三角関数で表すか指数関数で表すかについては,私も経験があるような・・・ 量子力学では,本質的に波動関数は複素数になりますが,この問題はエネルギーが一定の定常状態の問題で,時間の関数の部分で複素数であることを吸収できますから,実際に解くシュレディンガー方程式の解は実数でよいはずです. シュレディンガー方程式を解いて出てきた解は,三角関数でも,それをオイラーの公式でまとめた指数関数で表してもかまいません. しかし,実数である波動関数を両者の表現で一致させるためには,指数関数を使うときは線型結合の係数が複素数でなくてはなりません. それで,オイラーの公式による指数関数を使う場合だと,境界条件を適用したときに難しくなる(未知数が増える)ので,一般に三角関数を使うのだと思います.
> でもこうしてこの問題にトライしていると,半導体工学が進歩して,いうならば人工分子といっていいような素材開発がされている現代では, > このような「有限量子系」のモデル計算としての今回の問題は意外と良いものだなあと感じました.
確かに,量子力学を学ぶ上で,井戸型ポテンシャルの問題は絶対に外せませんね. 量子力学は,学ぶ順番やテキストによって,かなり印象(非常にわかりにくい,難しいけどなんとかなる)が変わってくると思います. 中には井戸型ポテンシャルの問題の前に,調和振動子(しかもエルミートの微分方程式を級数展開で解く)を先に説明しているテキストもあります. こうなると運ですね(笑)
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/04(Thu) 12:29)
>微分方程式の解で,三角関数で表すか指数関数で表すかについては,私も経験があるような・・・
そうですね,オイラーの公式には随分とお世話になってきて,その利用テクニックには自信があったのに,盲点でした,_oRz.
>確かに,量子力学を学ぶ上で,井戸型ポテンシャルの問題は絶対に外せませんね. >量子力学は,学ぶ順番やテキストによって,かなり印象(非常にわかりにくい,難しいけどなんとかなる)が変わってくると思います. >中には井戸型ポテンシャルの問題の前に,調和振動子(しかもエルミートの微分方程式を級数展開で解く)を先に説明しているテキストもあります. >こうなると運ですね(笑)
我が国は,半導体立国でもあり,てっきり「量子力学の教科書」はギンギンに理解しやすい良書が沢山でているものと思っていました.
結局,物理の部分の論議と,数学の部分の論議とがバランス良く仕上げ難いのでしょうかね.
Re: 一次元箱形ポテンシャル
なんとなく さんのレス (2009/06/04(Thu) 14:53)
>mNejiさん,みなさん
なんとなくです.四方山話の程度で聞いてください.
この問題は初等量子力学の計算例題として比較的簡単で初期に出て来るものですが,基礎的で重要な問題ですね.物理が専門だった私も当然,学生の頃に遭遇し,一応は解いたのですが,エネルギー固有値が数値計算に頼らねばならないのをそのときは不愉快ながら受け容れていました.しかしエネルギー固有値を求めさせるとしたら高度な問題になります. その後,物性論の方(私のところでは物理と物性は別だったのです)で伝導体の計算にこの問題が出てくることを知り,そして力学でも既出であり,ちらりと記憶が蘇りました. 結局は,A+Bsin(x)=xなる超越方程式の根xを求めるわけですが,これはKepler方程式であり,xはBessel関数で(級数として)閉じた形に書けます. 初等関数による解析解が存在しないことには変わりないのですが,パラメータの大きさによる評価には関数形が与えられることは絶大です. もうご存知だったかも知れませんが,このことを初めて知ったときは,目から鱗でした.歴史的には力学(天文学)が先ですが,特殊関数と物理学の深い関わりを示す,好例だと思いました. P.S.このことに間違いは無いですが,詳細はうろ覚えなのでご勘弁を(笑).
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/04(Thu) 23:01)
なんとなくさん,興味深いお話だと思います.
>結局は,A+Bsin(x)=xなる超越方程式の根xを求めるわけですが,これはKepler方程式であり,xはBessel関数で(級数として)閉じた形に書けます. >初等関数による解析解が存在しないことには変わりないのですが,パラメータの大きさによる評価には関数形が与えられることは絶大です. >もうご存知だったかも知れませんが,このことを初めて知ったときは,目から鱗でした.歴史的には力学(天文学)が先ですが,特殊関数と物理学の深い関わりを示す,好例だと思いました.
数学アレルギだった方ですので,初めて知った話題ばかりです.此れまでの所の計算メモを書き直したら,固有値方程式に使えそうな特殊関数を探してみます.
その上,「Kepler方程式であり」というのは面白いものですね.私には,特殊関数というのはマジックみたいなものか,数学の女神から物理屋への贈り物としか思えません.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/07(Sun) 01:23)
えりさん,
まだ全てを理解したとは言い難い状況ですが,此れまで判った事を述べます.
(1)固有値方程式と固有値
これは座標系の取り方に依らず,同一の結果を出せる様です.たとえば,束縛領域(ポテンシャルがゼロの領域)を 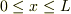 と言う座標系で表そうが,ポテンシャルの対称性と一致した
と言う座標系で表そうが,ポテンシャルの対称性と一致した 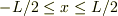 と言う座標系で表そうが構わない.
と言う座標系で表そうが構わない.
計算例:No.23907の前半.
- 固有関数
ところが,幾ら固有値を正しくだしても,波動関数の固有関数になると,ポテンシャルの対称性を反映した座標系, 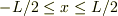 でないと,正しい定常解(三角関数)を導くことが出来そうにありません.
でないと,正しい定常解(三角関数)を導くことが出来そうにありません.
計算例:No.23907の後半.偶関数の結果までですが.
以上,ご参考まで.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/07(Sun) 10:16)
■指数関数の偶奇性(パリティ)
今回の計算を何度かやっているうちに, 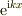 と
と  とでは振る舞いが違うのに気が付きました.で,この間の事情を整理してみます.
とでは振る舞いが違うのに気が付きました.で,この間の事情を整理してみます.
- 任意関数のパリティ
任意関数 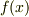 が在れば,いつでも
が在れば,いつでも
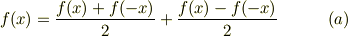
と書けると習ったと思います.右辺の前者がパリティが「+1」の偶関数,右辺の後者がパリティが「-1」の奇関数であるのは明らかです.
- 複素数の指数関数
事実,  に適用しますと,
に適用しますと,
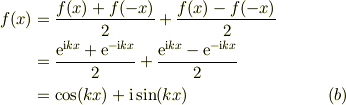
とオイラーの公式が出て来ます.まさに三角関数のパリティを反映している,と思われます.
- 実数の指数関数
同様に, 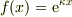 に適用しますと,
に適用しますと,
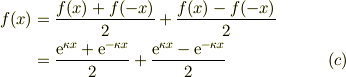
となります.すると,今回の計算に出て来た遠方解は指数部が正だけ,負だけの指数関数しか現れないので,パリティの固有関数にならない事になります.
ところが,ある定数 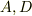 について
について
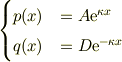
という関数セットがあるとすると,
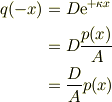
となります.従ってもし
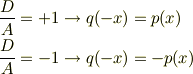
となる.
言い換えると,
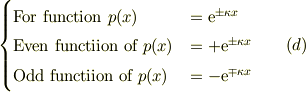
〜〜〜〜 ここら辺の考え方を簡単に解説している図書とかウェブ・サイトなどをご存知でしたらお教えくださいませんか?
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/09(Tue) 19:51)
大変に遅れましたが,計算ノートの改訂版を下記に示します.
固有値方程式の1次近似解までは求めましたが,固有関数の振る舞いを見るには,さらに高次の近似が居る可能性があります.ここら辺は,まだ未確認です.
〜〜〜〜〜〜〜〜〜〜〜〜 〜 計算ノートの改訂版 〜 〜〜〜〜〜〜〜〜〜〜〜〜 今回のノートでは,座標をポテンシャルが原点について対称になるように変更し,かつ束縛部分の波動関数を三角関数で展開する様にしました.
■座標とポテンシャル
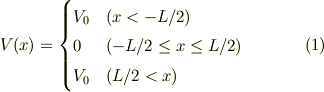
■波動方程式
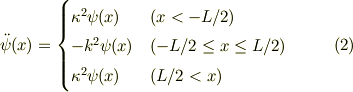
ここで,
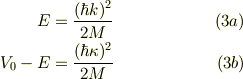
【ポテンシャルと波数の関係図】
<pre>
- ーーーーーーーーーーー

- ||↑
|||
|| |
|||
 |||
|||
|||
|||
||ー
|||
|||
|||
|||
||ー  || ↑
|||
|| ↑
|||  |||
|||
|||
|||
ーーーー+ーーーー−0 x=-L/2 x=0 x=L/2
</pre>
また,あとの便利の為に,

を定義すると,

となる.
■波動関数の展開
・左右の遠方で収束すること, ・束縛解は少なくとも三角関数型

■波動関数の境界条件
・ポテンシャルのジャンプ点での波動関数の滑らかな接続から, ・波動関数と導関数の連続性が成り立つ;

以下に,式(6)群を式(7)群に代入して具体的に解くが,記述の簡単さの為に,

を用いると,
![A\mathrm{e}^{-\kappa l} &= B\cos(-kl)+C\sin(-kl) \\&= B\cos(kl)-C\sin(kl) &\ (9a)\\\kappa A\mathrm{e}^{-\kappa l} &= k[-B\sin(-kl)+C\cos(-kl) \\&= k[B\sin(kl)+C\cos(kl)] &\ (9b)\\B\cos(kl)+C\sin(kl) &= D\mathrm{e}^{-\kappa l} &\ (9c)\\k[-B\sin(kl)+C\cos(kl)] &= -\kappa D\mathrm{e}^{-\kappa l} &\ (9d)](http://hooktail.maxwell.jp/bbslog/59e04822a1efc52a30a6a8c185a6782c.png)
を得る.そこで,Aを消去する為に 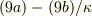 を取ると;
を取ると;
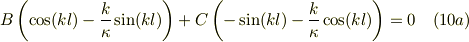
同様に,Dを消去する為に 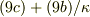 を取ると;
を取ると;

式(10a,b)はCの係数の符号だけが違うので,(B,C)のどちらか一方だけがゼロで,他方が非ゼロの解しか許されない事になる;
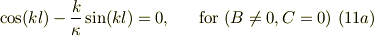
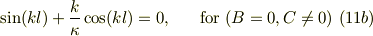
式(11a)は, 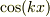 だけが許される,言い換えればパリティ=+1の関数,すなわち偶関数解の条件(固有値方程式)を示す.同様に,式(11b)は
だけが許される,言い換えればパリティ=+1の関数,すなわち偶関数解の条件(固有値方程式)を示す.同様に,式(11b)は 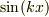 だけ,すなわち奇関数解の条件を示す.
だけ,すなわち奇関数解の条件を示す.
■ 波動関数の特徴
●偶関数解の場合
波動関数の係数は,式(11a)の係数条件と式(9a),(9c)より,
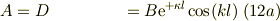
偶関数の左右に,同符号係数の指数関数で減少することが読み取れる.
●奇関数解の場合
同様に,式(11b)の係数条件と式(9a),(9c)より,

奇関数の左右に,異符号係数の指数関数で減少することが読み取れる.
■ エナジ固有値
● 偶関数の場合
式(11a)は波数kの方程式であり,式(5)と合わせて,次の固有値方程式の解である.
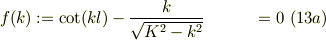
ポテンシャル障壁が十分に深くて,エナジ固有値より十分に大きい, 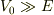 とすると,
とすると,

という状況の解を探索することになる.この具体的な解法は,No.23932の「予備ノート」に示した様に, ・ニュートン法, http://ja.wikipedia.org/wiki/%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%8 3%B3%E6%B3%95 を用いて逐次近似解を得る事が出来る.
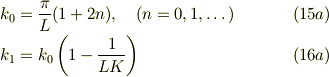
第ゼロ近似解の右端の値は;
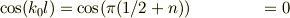
であるが,第1近似解, 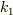 は,その内側になる.従って,波動関数は境界の少し手前から指数関数に接続するようにめくり上がると思われる.
は,その内側になる.従って,波動関数は境界の少し手前から指数関数に接続するようにめくり上がると思われる.
さらに,ゼロ近似解に出て来る,「量子数n」が大きくなるに連れて,真の解はゼロ近似解からのずれは大きくなる事が定性的に理解出来る.この事は,エナジ固有値が大きくなるに連れて,束縛領域から沁み出す成分が大きくなることと考えられる.
● 奇関数の場合
偶関数と同様に,次の固有値方程式の解である.
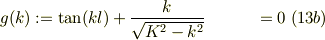
ゼロ近似解は, 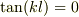 を満たすとして,ニュートン法により
を満たすとして,ニュートン法により 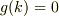 を第1近似解まで求めると,
を第1近似解まで求めると,
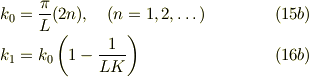
となる.
少なくとも第1近似解までの固有値では,パリティに依らず同一の結果となる.
#恐らく,厳密解でも固有値では,パリティ依存性は無いと推定出来そうだ.
● 偶奇合わせて
波数固有値を小さい順に 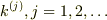 とすると,ニュートン法の第1近似の範囲で,
とすると,ニュートン法の第1近似の範囲で,


なお,式(5)より
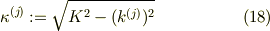
● 対応するエナジ固有値も,
![E^{(j)} &:= \frac{\hbar^2 [k^{(j)}]^2}{2M}\\&= \frac{\hbar^2 \pi^2 }{2ML^2}\left(1-\frac{2}{LK}\right)j^2, \qquad (j=1,2, \dots) &\ (19)](http://hooktail.maxwell.jp/bbslog/ad909ab282b04d55a918abb7989f1005.png)
■ 波動関数も固有値関数
式(6)より,第j準位の波動関数を  とすると,
とすると,
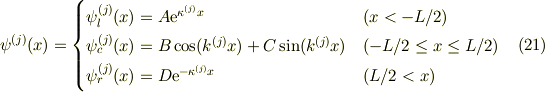
ここで,式(11a,b),式(12a,b)より, 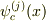 を定数
を定数  で書き換える;
で書き換える;
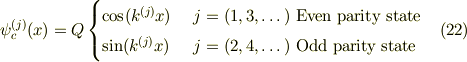
すると式(12a,b)も書き換えられて;
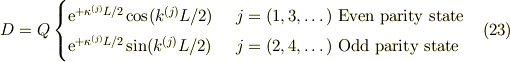
■存在確率の「束縛部分」と「沁み出し部分」との比
束縛部分の存在確率 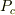 ,沁み出し部分の存在確率
,沁み出し部分の存在確率 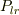 とすると
とすると
![P_c &:= \int_{-L/2}^{L/2}|\psi^{(j)}_c (x)|^2\mathrm{d}x &\ (a)\\ &= \int_{-L/2}^{L/2}Q^2\begin{cases}\cos^2(k^{(j)}x)\\ \sin^2(k^{(j)}x)\end{cases}\mathrm{d}x\\ &= \int_{-L/2}^{L/2}Q^2 [1 \pm \cos(2k^{(j)}x)]\mathrm{d}x\\ &=\frac{P^2}{2k^{(j)}} \int_{-Lk^{(j)}}^{Lk^{(j)}}[1 \pm \cos(\xi)]\mathrm{d}\xi\\ &=\frac{Q^2}{2k^{(j)}} [\xi \pm \sin(\xi)]_{-Lk^{(j)}}^{Lk^{(j)}}\\ &=\frac{Q^2}{2k^{(j)}} \left[2Lk^{(j)} \pm2\sin(Lk^{(j)})\right]\\ &=Q^2 \left[L\pm \frac{\sin(Lk^{(j)})}{k^{(j)}}\right]\\ &=Q^2 L \left[1\pm \frac{\sin(Lk^{(j)})}{Lk^{(j)}}\right] &\ (24a)\\ &\sim Q^2 L \left[1\pm \frac{\sin\left(\pi\{1-(LK)^{-1}\}j\right)}{\pi\{1-(LK)^{-1}\}j}\right] &\ \because (17a)\\ &\sim Q^2 L \left[1\pm \frac{\pm(LK)^{-1}\}j}{\pi\{1-(LK)^{-1}\}j}\right]\\ &\sim Q^2 L \left(1 + \frac{1}{\pi LK} \right) \qquad \text{ no dependence on j ?} &\ (24a')\\ P_{lr} &:= 2\int_{L/2}^{+\infty}|\psi^{(j)}_r (x)|^2\mathrm{d}x \\&= 2D^2\int_{L/2}^{+\infty}\mathrm{e}^{-2\kappa^{(j)} x}\mathrm{d}x\\&= 2D^2\left[\frac{\mathrm{e}^{-2\kappa^{(j)} x}}{-2\kappa^{(j)}}\right]_{L/2}^{+\infty} = \frac{\mathrm{e}^{-\kappa^{(j)} L}}{\kappa^{(j)}}D^2\\ &= \frac{\mathrm{e}^{-\kappa^{(j)} L}}{\kappa^{(j)}}Q^2\begin{cases}\mathrm{e}^{+\kappa^{(j)} L}\cos^2(k^{(j)}L/2)\\ \mathrm{e}^{+\kappa^{(j)} L}\sin^2(k^{(j)}L/2) \end{cases}\\& = \frac{Q^2 L}{\kappa ^{(j)} L}\begin{cases}\cos^2(k^{(j)}L/2) \\\sin^2(k^{(j)}L/2) \end{cases}&\ (24b)\\&= \frac{Q^2 L}{k^{(j)} L}\begin{cases}+\cos^3(k^{(j)}L/2) /\sin(k^{(j)}L/2) \\ -\sin^3(k^{(j)}L/2)/ \cos(k^{(j)}L/2) \end{cases}&\ (24b')\\1 &= P_{c}+P_{lr} &\ (24c)\\ &= \frac{Q^2 L}{k^{(j)} L}\begin{cases}k^{(j)} L +\sin(k^{(j)} L) +\cos^3(k^{(j)}L/2) /\sin(k^{(j)}L/2) \\ k^{(j)} L -\sin(k^{(j)} L) -\sin^3(k^{(j)}L/2)/ \cos(k^{(j)}L/2) \end{cases}](http://hooktail.maxwell.jp/bbslog/100f915345a4cd47a1a4827d2e2ad4c7.png)
〜〜〜〜
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/22(Mon) 18:48)
■固有値の数値計算:メモ
No.24103 の計算ノートに沿って,数値計算をした結果を簡単に纏めます.実際の計算の結果が記載された資料が見当たらなかったので参考まで.ただし,完全かどうかは保証の限りではありません(笑).
#でも,間違いを見つけたらコメントを下さいね.
〜〜〜〜
計算ノートから関係部分を抜き書きします;
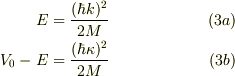



基底準位から順に 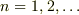 とラベルを貼ると,ポテンシャル障壁が十分に高い範囲では,その準位の波数
とラベルを貼ると,ポテンシャル障壁が十分に高い範囲では,その準位の波数 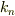 のゼロ近似解
のゼロ近似解  は,
は,
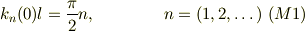
従って,固有値方程式は;
・寓パリティの解; 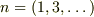 に対応.
に対応.
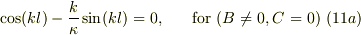
・奇パリティの解; 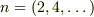 に対応.
に対応.

数値計算するにあたって,式(11a,b)の三角関数の中が 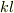 と無次元となっているのに対して,
と無次元となっているのに対して, 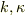 も比としてのみ入っているので,無次元変数を導入した方が,式の操作が簡明となる;
も比としてのみ入っているので,無次元変数を導入した方が,式の操作が簡明となる;

従って,固有値方程式も; ・偶関数解;
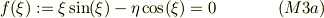
・奇関数解;
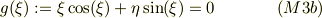
となる.よほど  で無い限り,単純なニュートン法での解法は問題ない.
で無い限り,単純なニュートン法での解法は問題ない.
それぞれの導関数は;
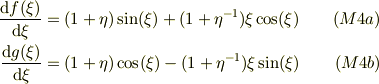
ニュートン法の漸化式は ・偶関数について;
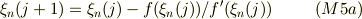
・奇関数について;
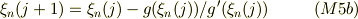
ただし,ゼロ近似解は;

● 実際の数値解
励起準位(n=1,2,3,4)について,漸化式の収束性をみたが,ほとんど 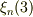 程度の近似で,
程度の近似で, 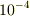 以下で収束していた.
以下で収束していた. 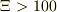 ほどだと
ほどだと 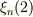 でも十分であった.
でも十分であった.
【表1 ξの数値】<pre> Ξ=5.7 Ξ=10 Ξ= 50 Ξ=1000 (π/2)*n n=1 1.334 1.428 1.540 1.569 1.571 n=2 2.657 2.852 3.080 3.138 3.142 n=3 3.947 4.271 4.620 4.708 4.712 n=4 5.154 5.679 6.160 6.277 6.283 </pre>
前回のノートの式(24a),(24b)から,非束縛率= 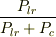 を求めた.
を求めた.
【表2 非束縛率】<pre> Ξ=5.7 Ξ=10 Ξ= 50 n=1 0.008 0.002 0.000 n=2 0.036 0.008 0.000 n=3 0.094 0.018 0.000 n=4 0.238 0.035 0.000 </pre>
以上.
Re: 一次元箱形ポテンシャル
mNeji さんのレス (2009/06/23(Tue) 14:49)
自己コメントです.
今頃になって気づきましたが,領域を(0〜L) としても波動関数は求まる様です.(-L/2 〜 L/2)の解とは平行移動するだけですから.計算の見通しが良い方をとるのは自然ですからね.
原理的に「座標の取り方には関係ない筈だ」という立場から,釈然としませんでしたが,これでやっとこの問題から解放されるような気がします(苦笑).
そこで,No.23907の立場(0〜L)で,固有関数を見直してみましょう.
〜〜〜〜〜〜 解くべきは,束縛領域の波動関数
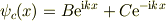
が,境界条件から得られる;
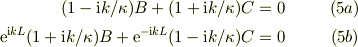
と,それらに基づく固有値方程式;
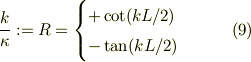
からどう表現されるかを検討します.
波動関数を三角関数に書き換え,
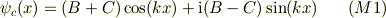
式(5a)を  に書き換えて,整理すると,
に書き換えて,整理すると,

故に,
![\psi_c(x) &= (B+C)[\cos(kx)+R^{-1}\sin(kx)] &\qquad (M3)](http://hooktail.maxwell.jp/bbslog/4c1a89b74f4a784d526ea85db4a637f8.png)
以下では,寓パリティの状態に対応する 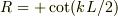 に限定して論議すると;
に限定して論議すると;
![\psi_c(x) &= (B+C)[\cos(kx)+R^{-1}\sin(kx)]\\&=(B+C)[\cos(kx)+\tan(kL/2)\sin(kx)]\\&=\frac{B+C}{\cos(kL/2)}[\cos(kx)\cos(kL/2)+\sin(kx)\sin(kL/2)]\\&=\frac{B+C}{\cos(kL/2)}\cos(kx-kL/2)\\&=\frac{B+C}{\cos(kL/2)}\cos\left(k(x-L/2)\right) &\qquad (M4)](http://hooktail.maxwell.jp/bbslog/e3f6252142ae1fd80e64314dbaab721b.png)
この関数は,No.24103の式(22)に示した;
『領域(-L/2,L/2)での寓パリティ関数, 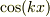 』
をx軸の正の方向に
』
をx軸の正の方向に 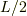 平行移動した関数である.
平行移動した関数である.
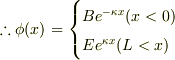
 の場合では?
の場合では?