流体力学で，ポテンシャルに関する式変形について

流体力学で，ポテンシャルに関する式変形について

はる さんの書込 (2009/05/23(Sat) 19:10)

流体力学の数式について質問です． ポテンシャルφがベクトル |0f7f0c35b5d4f171f5f2f032b2f55d64|A|cbb184dd8e05c9709e5dcaedaa0495cf| と距離 ｒ（ そしてｒ方向の単位ベクトル |0f7f0c35b5d4f171f5f2f032b2f55d64|n|cbb184dd8e05c9709e5dcaedaa0495cf| ） に対して次式の関係にあり，

\phi=\mbox{\boldmath |7fc56270e7a70fa81a5935b72eacbe29|}\cdot grad(\frac{1}{r})=-\mbox{\boldmath |7fc56270e7a70fa81a5935b72eacbe29|}\cdot\frac{\mbox{\boldmath |7b8b965ad4bca0e41ab51de7b31363a1|}}{r^2}\ \ \cdots \ \ (1)

速度 |0f7f0c35b5d4f171f5f2f032b2f55d64|v|cbb184dd8e05c9709e5dcaedaa0495cf| がφに対して次式の関係にある時，

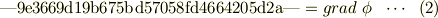
\mbox{\boldmath |9e3669d19b675bd57058fd4664205d2a|}=grad \ \phi\ \ \cdots \ \ (2)

速度 |0f7f0c35b5d4f171f5f2f032b2f55d64|v|cbb184dd8e05c9709e5dcaedaa0495cf| が，

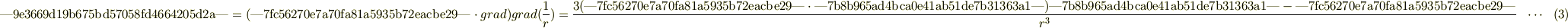
\mbox{\boldmath |9e3669d19b675bd57058fd4664205d2a|}=(\mbox{\boldmath |7fc56270e7a70fa81a5935b72eacbe29|}\cdot grad)grad(\frac{1}{r})=\frac{3(\mbox{\boldmath |7fc56270e7a70fa81a5935b72eacbe29|}\cdot\mbox{\boldmath |7b8b965ad4bca0e41ab51de7b31363a1|})\mbox{\boldmath |7b8b965ad4bca0e41ab51de7b31363a1|}-\mbox{\boldmath |7fc56270e7a70fa81a5935b72eacbe29|}}{r^3}\ \ \cdots \ \ (3)

で与えられるらしいのですが，導出過程が理解できません．

（３）式の最初のイコール，次のイコール，両方がわかりません．アドバイスよろしくお願いします．

ちなみにベクトル |0f7f0c35b5d4f171f5f2f032b2f55d64|A|cbb184dd8e05c9709e5dcaedaa0495cf| は物体の速度や形に依存するベクトルということですが，問題の段階では未定ですし問題では式変形しているだけですので任意の，とあるベクトルと考えてもらっていいかと思います．

Re: 流体力学で，ポテンシャルに関する式変形について

toorisugari no Hiro さんのレス (2009/05/23(Sat) 21:12)

\bm{A} を定ベクトルとして， \nabla\left(\bm{A}\cdot\nabla\left(\frac{1}{r}\right)\right) を地道に成分計算してください．

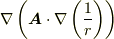\nabla\left(\bm{A}\cdot\nabla\left(\frac{1}{r}\right)\right) の i 成分は

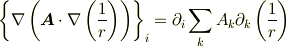
\left\{\nabla\left(\bm{A}\cdot\nabla\left(\frac{1}{r}\right)\right)\right\}_i&= \partial_i \sum_k A_k \partial_k \left(\frac{1}{r}\right)

となるので，これを計算していけばよいです．

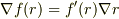
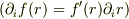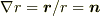
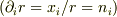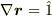
そのとき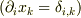， \nabla f(r)= f'(r) \nabla r (\partial_i f(r) = f'(r)\partial_i r) , \nabla r = \bm{r}/r=\bm{n} (\partial_i r = x_i/r = n_i) , \nabla \bm{r} = \hat 1 (\partial_i x_k = \delta_{i,k}) に注意してください．