はる さんの書込 (2009/05/23(Sat) 18:06)

ラプラスの方程式

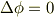
の解を求める場合に，無限遠でゼロという初期条件を設定している場合，その根拠は何なのでしょうか？

流体力学の非圧縮性理想流体で無限遠の速度はゼロだからということで，上記方程式を解いているのを見受けます． 現実の流体ではそうかもしれませんが，理想の理論を考えている場合では抵抗もないですし，減速要因が無いように思われます．憶測ですが，境界条件だけ現実を考慮しているのなら，それは不公平というかおかしなことだと思われ，しっくりきません．

詳しくは知りませんが電磁気学の静電ポテンシャルでも無限遠はゼロと置いてラプラス方程式の解をｒに反比例形にしているようですので，そちらを取り上げての解説でも構いませんので，みなさん，アドバイスよろしくお願いします．

toorisugari no Hiro さんのレス (2009/05/23(Sat) 18:34)

> 流体力学の非圧縮性理想流体で無限遠の速度はゼロだからということで，上記方程式を解いているのを見受けます．現実の流体ではそうかもしれませんが，理想の理論を考えている場合では抵抗もないですし，減速要因が無いように思われます．

はスカラーで速度ベクトルとどう関係してるか分かりませんが，例えば速度ポテンシャルと解釈します．

無限に広がる流体の中で，原点の近傍で物体が動く場合を考えます(原点近傍にわき出しと吸い込みの二重双極子がある場合に相当)．

物体近傍では流れが発生しますが，無限遠方ではどうでしょう? 抵抗などと関係なく，無限遠方は静止したままです．

それとも海で水泳をしたら，太平洋全体の水も動くのでしょうか?いったい何トンの水が動き出すのでしょうね．膨大な運動エネルギーを考えたら，人間の手の力では水泳さえできなくなります．

つまり，局所的な運動や作用は無限遠方には影響しない(事が経験で分かっている)ので，無限遠方では速度0，つまりポテンシャルを0とおいてかまわないのです．

# ちなみに無限遠で速度が0になるのは抵抗による「減速」でなく拡散です．原点から水がわき出す場合を考えます．放射状に広がる速度場が発生しますが，無限遠方では速度は0です．そうでないと十分大きい半径の球面を単位時間に通過する水の量がわき出し量を超えてしまいます(質量保存則より速さは距離の2乗に反比例します)． 流れが「広がる」から速度は無限遠方で0になるのです．

余談:

> ラプラスの方程式
>  |3eddcdf538fbe4d435b4463b3520951f| 
> の解を求める場合に，無限遠でゼロという初期条件を設定している場合，

方程式が定義されている領域が空間全体なら，上記の問題は普通あり得ないと思います．なぜなら無限遠でゼロという境界条件の下では，解は 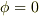しかないですから．

ポアッソン方程式 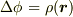なら，あるいは，ラプラス方程式が(例えば)原点以外で定義されているなら，無限遠でゼロという境界条件をつけた問題は良くあります．

はる さんのレス (2009/05/23(Sat) 20:09)

toorisugari no Hiroさん，早速の回答どうもです．

>余談以下

しかし書籍(ランダウ理論物理教程)では序盤各所でそう説明されています．筆者が何か含蓄をこめているのかもしれませんのでその辺もう少し考えてみます．

>例えば速度ポテンシャルと解釈します．

説明不足でしたが，速度ポテンシャルです．

>それとも海で水泳をしたら，太平洋全体の水も動くのでしょうか?いったい何トン >の水が動き出すのでしょうね．膨大な運動エネルギーを考えたら，人間の手の力で >は水泳さえできなくなります．

質問の具体的な対象は，非圧縮性理想流体の力学でして，その場合，流体をかなり理想化しています．もし抵抗などの余分な力が働かない（粘性無し，断熱，etc)のならば，遠くまで運動するのにエネルギー変化もないのではないかと思います．

>物体近傍では流れが発生しますが，無限遠方ではどうでしょう? >抵抗などと関係なく，無限遠方は静止したままです．

流れではありませんが，例えば，宇宙という，空気抵抗のないといわれている空間を動く物を想像すると，初速があれば無限遠まで苦も無く運動するのではないでしょうか．そんな風に理想流体を考えると，無限遠ゼロに疑問が生じるわけです．

実は私が当初妄想していたのは，原点に立つ人からみれば無限遠方の動く物体は静止しているようにしか見えないのと関係があるのだろうか，ということでした． しかし，頂いたレスを読んで別途思いついたのですが，どんな力にせよ無限遠まで影響が伝わるには相当な時間を要するのと何か関係があるのでしょうか．ポテンシャルとかベクトル量とかは結局，力ありきの理論のような気がします．特に問題の場合は力学の一種ですので．無限遠に力がかかって結果として生じた運動が，減衰や抵抗などがなくスムーズに原点に伝わってくるとしても，距離や時間が無限（＝いつまで経っても到達しない）な為，その運動の原点への影響，原点付近の状態との関係は，ゼロ．そういう哲学が背景にあるのか？とも思ったのですがいかがでしょうか．

toorisugari no Hiro さんのレス (2009/05/23(Sat) 21:05)

> しかし書籍(ランダウ理論物理教程)では序盤各所でそう説明されています．筆者が何か含蓄をこめているのかもしれませんのでその辺もう少し考えてみます．

ランダウは行間を読まなければいけない本です．また，数学的にはルーズな記述がみられます．

> もし抵抗などの余分な力が働かない（粘性無し，断熱，etc)のならば，遠くまで運動するのにエネルギー変化もないのではないかと思います．

抵抗がない場合でも，無限遠方で速度0でないなら，運動エネルギは無限大になり，考えてる現象の仕事は無限大になります．抵抗で散逸する場合も熱エネルギーを考えれば同様の矛盾が発生します．

局所的で有限な仕事の作用では，その影響による空間全体の運動は起こりようがありません．

>宇宙という，空気抵抗のないといわれている空間を動く物を想像すると，初速があれば無限遠まで苦も無く運動するのではないでしょうか．

なにもないのに運動が遠方まで伝わるはずがないです．

はる さんのレス (2009/05/23(Sat) 22:43)

toorisugari no Hiroさん，早速の回答どうもです．

まず，No.23830の最後の段落（妄想の部分）を一部修正しときます．修正前の文は無限遠の力が伝わってくるという表現でしたが，軽率な表現でした．無限遠で生じた運動が，という表現に直しておきます．

＞抵抗がない場合でも，無限遠方で速度0でないなら，運動エネルギは無限大に ＞なり，考えてる現象の仕事は無限大になります．

すいません．いわれている事がよくわかりません．たとえば数式でそれを表現できるのなら，数式で詳しく示していただけませんでしょうか．（馴染みの関係式とかだったら理解しやすいかもしれないので．）

私があげた宇宙での運動の例を別の，更に馴染みのある例で代用しますと，たとえば，高校物理のいわゆる等速直線運動などは，理想ですが，この理論では無限遠まで行っても速度はゼロにならないのではないでしょうか？もちろん，無限ですから到達しえないのですが，等速運動しているものがゼロになるというのなら，どの辺りから減速がはじまるのか？又はどのあたりから停止するのか？ということです． それとも(先生は教えてくれなかったけど)実は無限遠では等速がゼロになる(という設定な)のでしょうか？

よろしくおねがいします．

toorisugari no Hiro さんのレス (2009/05/24(Sun) 10:34)

粒子の速度が慣性の法則で保存することと，圧力の効果で物体の運動が流体に広がることを混同されているように思えます．

> 高校物理のいわゆる等速直線運動などは，理想ですが，この理論では無限遠まで行っても速度はゼロにならないのではないでしょうか？

無重力で真空中なら(流体が存在しないなら)，粒子が等速直線運動しているとき，その粒子が無限遠方にいっても，その粒子の速度は変わりません(0でありません)．

しかし，摩擦のない流体中で，有限の物体が有限の速度で動いたとき，周りの流体に発生する流れの変化は無限遠方までは届きません． # そもそも物体近傍の流体は物体から離れると速やかに速度は拡散して0になり，遠方まで流体粒子は届きません．

全く，関係ない話です．

toorisugari no Hiro さんのレス (2009/05/24(Sun) 10:51)

>> 無限遠方で速度0でないなら，運動エネルギは無限大になり，考えてる現象の仕事は無限大になります． > いわれている事がよくわかりません．たとえば数式でそれを表現できるのなら，数式で詳しく示していただけませんでしょうか．（馴染みの関係式とかだったら理解しやすいかもしれないので．）

数式だから分かる，とは思えませんが...

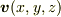を流体の密度， を流体の速度ベクトル場とします．

最初に流体が静止しているなら，静止系からみた流体全体の運動エネルギ

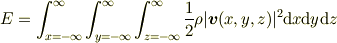
は，速度がいたるところで0ですから，0です．

誰かが原点近傍で水泳をして流れが発生したとします(別スレッドの問題がそれにあたりますね)．そのときの流体全体の運動エネルギは有限でなければいけません( 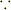人力は有限)．

もし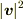， が無限遠方で0でないなら(距離の-3乗より速く0に近づかないなら)，上の積分は発散して，運動エネルギは無限大となり矛盾します．

# 本当は上の積分領域は泳者以外の領域としなければいけませんが，今議論してるのは無限遠方の振る舞いなので，その件は無視します．

はる さんのレス (2009/05/29(Fri) 00:19)

toorisugari no Hiroさん，回答ありがとうございます．

toorisugari no Hiroさんの意見はそのとおりですが，私の疑問は流体力学の本で問題のテーマが出てきたときに，それ以前に説明されている定義や仮定，公式とどう折り合いがついているのか，というものです． No.23827はそう言う意味で質問しました．これは，残念ながら，例えば私が対象としているランダウや今井 功さんの本を手にして参照しないと事実上正確な議論はできないでしょうから，以下で変なこと言ってると思っても，その辺も考慮していただくとありがたいです．

明記していなかったので誤解を生じたかもしれないことを説明しておきますと，無限遠でゼロの初期条件が出てくるのは，主に球（や円柱）の周りのポテンシャル流を求める問題です．流線が直線で何本も引かれていて，球の周りだけは球面に沿ってカーブしているような図が添えられています．(放射状などではなく，)基本，Ｘ方向への流れです．このカーブしている流線上の流体粒子の速度が無限遠でゼロになるというのが分からなかったわけです．

当初やりとりさせてもらった後，色々と新しい理工書をあたってみたのですが，中には分かりやすい本もあり，toorisugari no Hiroさんとの会話と合わせて，おかげさまで抱いていた問題の理由がわかってきました．

まずヒントとなったのは，最近の本では，上記の物体の周りの流れを解くのに，「一様流」と「湧き出し，吸い込みの流れ」の線形結合として解いているということでした．そして，一様流を座標変換して静止に持ってくれば，一様流の無限遠では速度ゼロ，ということです．そして，理想流体の理論で最初に既出の質量保存則．

「湧き出し，吸い込みの流れ」では，その湧き出し吸い込みの場所は点ですから，質量保存を考えると，その点から離れれば通過断面積は拡大し，流量保存を考えれば速度は遠方でゼロにならざるをえません．Ｘ方向流れとは言っても，1次元ではないので，湧き出し点の点との差異が効いています．

それと，騙されていたのは，球の周りで湾曲して左右に無限遠へとつながっている直線の挿絵です．この流線に沿って無限遠から無限遠へ流れる流体粒子が，ベルヌーイの定理と質量保存を満たしているので，同じ流線上で無限遠方で相対速度ゼロなのに球の周りで動いているというのはおかしいです．途中で外力が加わらない限り．しかし初期の理論ではそうだといえそうな外力は考慮されてないので，やはり動いているのはおかしいです． つまり，上の沸き出し等を含めた説明を考慮すると，無限遠へと流れる流体粒子は球の周りでも速度変化しておらず，速度ｖなら常にｖ，静止なら常に静止ということです．そして球のまわりで湾曲する流れには，挿絵には描かれていないが実は球の周りをぐるぐる回る流線上の流れがあり，それには湧き出し吸い込みの理論で説明され，その流れに関しては無限遠で速度ゼロ，だということです．そして，その挿絵には書かれていないぐるぐる回る流れのみこそが，問題で問われている流れだということです．球の周りの流れを解く問題であり，無限遠での境界条件が使われているものの，無限遠から流れて来た流体粒子（＝挿絵の平行直線群）が問題で解こうとしているその球の周りの流れに関与しているわけではなかったというわけです． まだ誤解もあるかもしれませんが，一応，モヤモヤは晴れました．

別件でgradの式変形を教えてもらっていましたが，それはまだ解けていません(汗；)．本屋でズバリの解説をやっとみつけましたが，家にかえると忘れてしまうのです(汗；)．がんばります．

なんとなく さんのレス (2009/05/29(Fri) 01:56)

>はるさん なんとなくです．よく勉強されていることが感じられて感心します．私は流体力学はさぼりすぎて良く知らないのですが，いくつか疑問点があったので，良ければ教えて下さい． この問題は電磁気学では非圧縮非粘性流体と思えば，アナロガスに一様平行電場中に置かれた導体球（円柱）周りの電場の問題と捉えられる気がします． そうすると電磁気学では一様電場と導体中の等価電荷（湧き出しに相等しますね）による電場の線形結合で表され，その結果を用い，遠方では電場は”０ではなく”一様電場になるという境界条件で解かれます．流体力学でも同じように考えることが出来ると思うのですが．これが書かれている外場とぐるぐる回ると表現されている速度場を分けて考える思想と（結果的に同じでも）違和感を覚えます． 確かに同時境界条件で与えられることがあるかも知れませんが，一般的とは言えない気がします． それとそのぐるぐる回る速度場は本当にあるのでしょうか．上の電磁場の場合は回転（ROT）なし，つまり渦無しですが，ラプラス型の解は通常スカラー場であり，そのようなベクトル場となるのでしょうか． 的外れな質問かも知れませんが，別の観点になるかも知れませんので．

toorisugari no Hiro さんのレス (2009/05/29(Fri) 10:23)

> 騙されていたのは，球の周りで湾曲して左右に無限遠へとつながっている直線の挿絵です．

> この流線に沿って無限遠から無限遠へ流れる流体粒子が，ベルヌーイの定理と質量保存を満たしているので，同じ流線上で無限遠方で相対速度ゼロなのに球の周りで動いているというのはおかしいです．

おかしいとは思いません．

> 同じ流線上で無限遠方で相対速度ゼロなのに球の周りで動いているというのはおかしいです．途中で外力が加わらない限り．しかし初期の理論ではそうだといえそうな外力は考慮されてないので，やはり動いているのはおかしいです．

内力，つまり，圧力の影響をお忘れです．

はる さんのレス (2009/06/01(Mon) 20:51)

なんとなくさんへ

>そうすると電磁気学では一様電場と導体中の等価電荷（湧き出しに相等しますね） >による電場の線形結合で表され，その結果を用い，遠方では電場は”０ではなく” >一様電場になるという境界条件で解かれます．流体力学でも同じように考えること >が出来ると思うのですが．

ただ，流体力学，少なくとも初歩の理想流体の場合は，その一様の場を，静止と考えることが数式的に可能です．数式的にとは，座標系の取り方を変えればそのようにでき，実際に専門書内に一様流の場合とそれが静止している場合の２通りに書かれた式が提示されているということです．電場と電荷の場合だと，その相互作用こそがテーマなわけですから，座標のとり方によっては電場0と設定できるなどとすると理論自体成り立たなくなるのではないでしょうか？

>それとそのぐるぐる回る速度場は本当にあるのでしょうか．上の電磁場の場合は >回転（ROT）なし，つまり渦無しですが，ラプラス型の解は通常スカラー場であり， >そのようなベクトル場となるのでしょうか．

ぐるぐる回るからといって何でも渦ありということにはならないようです．No.23913の漢字を「回る」でなくて「周る」とした方がよかったかもしれません．もちろん，その場の微小要素上において，rotの対象（ｖ）が，それ自体そこでぐるぐる回転しているのなら渦ありということになりますが．それに関しては，私も人に説明できるほど理解しているとはいえませんし，ここで一言で説明しにくいです． No.23913において，等速運動中に湧き出しと吸い込みを考慮すると，ぐるぐる周るような流線になるという理論を参照しましたが，一様流と湧き出し(吸い込み)それぞれは，定義から渦なしです．それを線形結合すると，球の周りではぐるぐる周るようです．

>的外れな質問かも知れませんが，別の観点になるかも知れませんので． いえ，観点の提示は助かります． 電磁気学も勉強すれば多いに参考になるのはわかっていますが，自分ではなかなか本腰を入れれないところがありますので，他の方の指摘は参考になります．

はる さんのレス (2009/06/01(Mon) 21:42)

まだ途中ですが，時間もかかりそうですし，一応，当初の疑問No.23827に対する，暫定的な自分なりの解釈をまとめておこうと思います．

>無限遠でゼロという初期条件を設定している場合，その根拠は何か？

初期条件をそう言う風に与えている，ということ．もしくは，無限遠で静止していない場合は静止するように座標系をとってやる，ということ． 時々，自明の理のように『無限遠で速度ゼロだから』と唐突に書かれているものがあるが，それはそういう意味であった． 当初自分が読んでいたランダウの本でもそういう表記があったのだが，よく原本をきちんと読みこんでみると，別の項目でそのように説明がなされていた．(ex.英語版2版改訂版p26,27)

>非圧縮性完全流体の系ならば，物質周りで速度（運動量）を持っている流体粒子は，そのまま無限遠方までその速度を保ち続けるのではないのか？という疑問について．

これは，ダランベールのパラドックス辺りの理論で，間接的に説明されていた． 『もしも理想流体中で均一に運動している物体を通りすぎるポテンシャル流というものがあるのなら，（式変形の結果より）無限遠まで考えた全体積における流体の運動量Pは一定，そして流体に働く力Ｆはゼロになる．これは物体に働く抗力，揚力が存在しないということであり，流体により物体に働く圧力は・・・（以下略）』 元々一様流である遠方の流体粒子は，一様流を静止ととらえれば，いつも静止しており，そこへ球がやってくると，球により球の表面をツルんと滑るような運動を生じさせられて，球が通りすぎればまた静止する．多少乱暴な書き方かもしれないが，非圧縮性理想流体中で均一に運動している物体を通りすぎるポテンシャル流というのは，そういう取り扱いをされていると理解しました．

toorisugari no Hiro さんのレス (2009/06/02(Tue) 11:24)

> 一様流と湧き出し(吸い込み)それぞれは，定義から渦なしです．それを線形結合すると，球の周りではぐるぐる周るようです．

ぐるぐる回りません．

x軸上に湧き出しと吸い込みを近くに置くと，二重双極子になります．これは磁石の磁力線と同じ流線を描きます．

これにx方向の一様流をくわえると，ある円を境に二つの領域に分かれます． 内側の領域は円の中に閉じこめられた磁石の磁力線と同じ流線を描きます． 外側の領域は円をよける流線を描きます．

「ぐるぐる周る」流れは「循環」がないかぎりあり得ません．

toorisugari no Hiro さんのレス (2009/06/02(Tue) 11:59)

> そういう取り扱いをされていると理解しました．

理解の順番が逆ですね．「つるん」とした動きになるのは，無限遠方で速度が0になることから導かれるのであって，「つるん」とするから無限遠方で速度が0になるのではありません．

静止している流体の中に等速直線運動する有限体積の物体をいれて運動を維持したら，無限遠方の速度は0と異なるのでは? あるいは 速度 の一様流の中で有限体積の物体を固定したら，無限遠方の流れは と異なるのでは?

というはるさんの疑問にたいする答えは否です． 理由は「経験でそうなっているから」がたぶん一番正しいです．

我々は水や空気の中で自由に運動できることを経験で知っています．動くための仕事は有限ですので，エネルギー保存則から考えて，流体のエネルギー変化は有限でなければいけません．よって，流体の速度変化は無限遠方までは及びません．

ダランベールのパラドックスは非粘性流体の話ですが，上の論理は粘性流体でも使えます．水や空気が，自由に変形できる「流体」であればよいのです．

すなわち「何故無限遠方の速度は変化しないのか?」の答えは 「 水や空気は流体である(経験則)から． 」です．

流体は自由に変形できるので，有限のエネルギー変化で物体の存在や運動を許容できるのです．

たとえば，無限の大きさの『剛体』が速度 で「流れて」いるところに，原点付近で「ピン留め」をする場合を考えます．剛体ですから一部が停止すると，無限遠方までの全体が瞬間的に停止します(非相対論)． このときの運動エネルギーの変化，つまり，ピン留めの仕事は無限大です． # つまり，剛体の中では我々は泳げません．

しかし，『流体』は一部をピン留めされても，他は変形して迂回してながれることができます．無限遠方まで影響を及ぼさないで対応することが，有限のエネルギー変化で対応することが，できるのです． # つまり，流体の中では我々は泳げます．

## まあ，現実の剛体は「無限遠方までの全体が瞬間的に停止」せずに，ひずんだり，ひび割れ等の破壊を起こして，有限のエネルギーの変化で対応します．しかし，ここでは理想的な「流体」と「剛体」で考えています．

なんとなく さんのレス (2009/06/02(Tue) 12:45)

>はるさん

レスを有難うございます． 私が言うのも何ですが，Hiroさんの説明は的確であり，示唆的です．自分なりの解釈や理解を考えることは素晴らしいのですが，是非Hiroさんの示された内容を吟味されることをお勧めします． 余談ですが，流体力学は兎も角，実際の流体解析には仕事上多少関わりがあり，流れのシミュレーションや実際の映像などを通じていろいろ面白い現象を見てきました．数学ではない物理として見る視点を養うことは非常に大切だと思いますね．

はる さんのレス (2009/06/02(Tue) 20:37)

toorisugari no Hiroさん なんとなくさん

いつも早いレス，感謝です． ちょっと，やはり私の理解不足と私の質問の説明下手がずっと原因になって，話が噛み合わないことが多いのがとても残念です． ものすごく長文，それも物理とは関係ない；，になりそうなのですが，やはりレスをいただいた方々に答えるのが礼儀ですし，レスさせていただきます．

>是非Hiroさんの示された内容を吟味されることをお勧めします． Hiroさんのレスはいつも非常に参考になっています．先達の指摘内容ですから毎回，吟味しています． ただ，すべての感想や吟味内容を書くと，レスの量が３倍以上になってしまうのは目にみえていますから，掲示板には私に都合のよい要点だけ書いて，あとは疑問を解決する為の追加質問を簡潔にしてきた次第です． また，指摘された一部事項は保留にすることもあります．それは考える時間や気になる事を調べる時間が必要だからです．いわれてすぐ納得したり，そうですか分かりました，といかないのが大学レベルの物理のつらいところだと感じています；．ですから，頂いた指摘にしばらく回答しなかったり，重要な指摘には触れずに他の一部事項に対してのみ返答していることが私にはよくあるかと思いますが，それはそういう事情です． ただ，そのようになんとなくさんが指摘されたということは，HIROさんの指摘を私が無視しているかに皆さんには見えるということでしょうから，その辺，皆さんにご迷惑をかけていることは謝ります．

No.23976とNo.23978では，本当はレスできる段階ではなかったのですが， なんとなくさんがNo.23919で >いくつか疑問点があったので，良ければ教えて下さい． と質問形式でレスされているので，あまり待たせては失礼だと思い，その件に返答し，あと，次にレスする時がいつくるか分からなかったので，ついでに見解を述べたのです．（先に述べたように指摘の咀嚼，追加調査，自分の疑問の整理，自分の解釈への批判等に時間を要するため．）

次のレスにtoorisugari no Hiroさんの指摘への私のレスも（出来る段階ではありませんし，やっても泥沼になりそうな気もしますが，がんばって），返信しておきます．

はる さんのレス (2009/06/02(Tue) 23:25)

toorisugari no Hiroさんへの返信です．

まず，最もはっきりさせておきたいこと，つまり私の元々の一番の疑問『理想流体の話の中で，無限遠で流速がゼロという文言が唐突にでてくるが，その理由は？』に関してですが，これは物体が運動する一様流の系を静止系に選ぶから無限遠で静止と書かれていた，という事で話の筋として，なんとなくさんも，Hiroさんも，異論ないと思います．実は本にそう説明されていましたでは拍子抜けでしょうが，当事者としてはこのことを見つけるのにかなり苦労しました．これは解決しました．

あとは，話し合いの過程などで出てきたその他の私の解釈に対する意見の相違が残っている，というところでしょう． 一度，全てのいただいたレスへの私のレスの下書きを試みたのですが，あまりに長くなってきましたのでやめました．それを出すと課題や誤解が増えるだけで収拾がつかないですから．私の第一の疑問が解決しただけで実質このスレはおわりにさせてください．

ですが，No.23987を参考にさせていただきますと，頂いているレスにノーコメントでは失礼の感（無視，自論に篭っている様相）をあたえてしまうのかもしれませんから， 主だった点だけは簡単に載せておきます．読み流してください．

>理解の順番が逆ですね．「つるん」とした動きになるのは，無限遠方で速度が0に >なることから導かれるのであって，「つるん」とするから無限遠方で速度が0にな >るのではありません．

悲しいことに，今回頂いた意見にはとくに誤解が頻発しています．これはコミュニケーションの問題ですから，日本語の問題ですが；ネットの文字伝達はつらいです；．まあ，私のスレのテーマの異常さにも原因があるのでしょうが；． 上記レスについてですが，私の解釈は指摘いただいている意味で書いておりましたよ；． ぐるぐるという表現も私の日本語力のなさを実感しています．二重極の図をリンクしてこのようです，と誤解を抑えるような表現をトライしたのですが，ネットで見つけれなかったのでああなり，結果，予想以上の誤解を生んでしまいました＞＜． 周辺の他のご指摘にかんしても，まさに指摘の通りなのですが，しかし，私の真意を誤解されているのです．間違っているといっているのではないです．そんな立場でもないし，頂いた意見に疑いもありません．この齟齬はもう，しかたないと思っています．

理想流体非圧縮性ポテンシャル流においての一様流中の球周りと無限遠での振るまいについては，たとえばランダウの本にも，そこで取り扱っておきながら，隣で，実はそのような(球の周りでの)流れは存在しえないと理論の問題点をかなり詳しく書いています．更に，ランダウだけでなく別の著者も説明しているように，ダランベールのパラドックスの項でも，そういう流れの理論の矛盾点が説明されています．それを応用すれば私の抱いた問題にも行き当たります．最初読んだときは何の感慨もありませんでしたし，本件とも関係ありそうでないかなと思っていましたが，後で事の重要性を理解してくると，昔の人も似たような疑問を抱いてあたふたしたんだな，と微笑んでしまいました．同時にそういう世界にぐっと近づけたように感じたものです． 問題だ矛盾だといってますが，もちろん，皆さんご存知のように，だから間違っているというのではなく，理論を広げれば後々解消される矛盾です（私は最後まで極めていないのでそう断言するのはおかしいですが．）．ですが，後々そうでも，この時点では，おかしいところが多々ある特殊理論であるということを知っておく必要があります．

私が非粘性流体や他のことへ勉強を進めていけば，いずれtoorisugari no Hiroさんのような意見になることは十分予想しています．また力学や熱力学の知識だけで判断してもtoorisugari no Hiroさんの指摘は全くおかしくありません．しかし，私が対峙している疑問はそういうところではないので，なかなか折り合いがつかないということです．．（気をつけていることは，その場その場で仮定や定義を認識すること．自己参照みたいな状態にならないことです．AだからBといい，後でBだからAということになっていたら大変です．だからその場その場で最初の定義からきちんと論が運ばれているのかを重要視します．） 指摘は，前レスにも書いていますが，どれも参考になっています．新しい知識，補完や思いこみの修正，きっかけ等，いろいろ役立ちます．

実際，この話題は，いまの理解度のままで保留するのが自分としては一番だと薄々思っているのです．ですから，勝手ですが，私としてはこれで締めにしておきます． ありがとうございました．

私の表現が誤解を生んだということは結局，自分の理解に荒がおおいということの現れです． 人に理解させることができて初めて理解しているといえる，って箴言がありますから．

>なんとなくさん 学問は目下趣味です． なんとなくさん同様，携わったのがきっかけで後付けで理論をやっています；別件で数学のレスをしたので数学徒と想像されたのでしょうか？（笑）数学も素人です；．

なんとなく さんのレス (2009/06/03(Wed) 00:13)

>はるさん

私の方は了解しました．工学系の学徒とばかり想像していました．私の学生時代は理論物理学でしたが，理系の発想とは少し違うな，とは感じました． 既に書いたとおり，流体力学はとおり一辺の学習しかしておらず，お恥ずかしい限りですが，五十の手習いでぼちぼちやる予定です（笑）．ではまたの機会に．

toorisugari no Hiro さんのレス (2009/06/03(Wed) 01:00)

状況は理解できました．

つまり，任意の流れの問題を解くのに，無限遠方で速度0という境界条件を課すのは一般性を失っているのではないかというのが，本当の疑問なですね．

ガリレイ変換をすれば無限遠方で一様流に近づく流れは，無限遠方で速度0に近づく流れに変換できるので一般性は失われないですね．

ともかく，無限遠方の境界条件を設定する場合，暗黙のうちに質量保存則やエネルギー保存則やガリレイ普遍性などの物理原理を使っているということです．

# 静水中で物体を動かしたり，一様流中に物体を置いた場合，無限遠方が静水，あるいは一様流になる保証は本来ありません．しかし，そのような場合でも，流体の性質や保存則を考慮すると，無限遠方が静水，あるいは一様流になることが導けるというのが，私の記事の骨子です．