静電場について
静電場について
digi さんの書込 (2009/05/22(Fri) 05:15)
静電場についていくつか質問があります.
a)電荷q1があるとき,電荷q2を無限遠からaまで(aはq1からの距離)まで運ぶのに必要な仕事は, 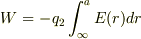 とあらわされると思います.E(r)はq1が作る電場ですが,q2を動かしたらE(r)は変化するのかな?と考えてしまい混乱しています.ふつうは
とあらわされると思います.E(r)はq1が作る電場ですが,q2を動かしたらE(r)は変化するのかな?と考えてしまい混乱しています.ふつうは 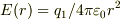 だと思いますが,q2の電場ががE(r)に影響を与えたりしないのでしょうか?
だと思いますが,q2の電場ががE(r)に影響を与えたりしないのでしょうか?
- a)とちょっと関連しますが.電荷q1とq2があるときの静電ポテンシャルについてです.ふつうに考えたら,q1はq2の電場によるポテンシャルエネルギー
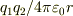 (rは電荷間の距離)を持っていて,q2も同じポテンシャルエネルギーをもっているから,この系の静電ポテンシャルは
(rは電荷間の距離)を持っていて,q2も同じポテンシャルエネルギーをもっているから,この系の静電ポテンシャルは 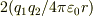 でいいのではないですか?でも,参考書をみると,「q1とq2を無限大から運んでくることを考える.まずq1を無限大から運んでくるときは電場はないから仕事は0.つぎにq2を運んでくるときはq1の電場があるからその分仕事が必要で,静電ポテンシャルは
でいいのではないですか?でも,参考書をみると,「q1とq2を無限大から運んでくることを考える.まずq1を無限大から運んでくるときは電場はないから仕事は0.つぎにq2を運んでくるときはq1の電場があるからその分仕事が必要で,静電ポテンシャルは 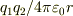 」と書いています.参考書によれば,私の考えは同じポテンシャルを2回数えているようです.でもどちらの電荷もポテンシャルを持っているような気がして仕方ありません.
」と書いています.参考書によれば,私の考えは同じポテンシャルを2回数えているようです.でもどちらの電荷もポテンシャルを持っているような気がして仕方ありません.
よろしくお願いします.
Re: 静電場について
ミュフ猫 さんのレス (2009/05/22(Fri) 11:04)
digiさん,こんにちは.
私も同じ疑問を持ってます.ですから,正しい解答は他の方々にお願いします.
a)について,もし,電荷に大きさがあれば,自身の放つ静電場も考慮する必要が あるのではないでしょうか. 点電荷の場合,大きさが無く,無限大の電荷密度を持つ仮想粒子なので, 仕事を計算する際,そのような自己力を無視してよいのかもしれません.
b)について,静電ポテンシャルとは,二つの荷電粒子が共有するエネルギー なのではないでしょうか. ですから,空間に三つの荷電粒子が存在すれば,三つの静電ポテンシャルが, 四つならば,六つの静電ポテンシャルが,n個ならば,n*(n-1)/2個の静電 ポテンシャルが存在すると考えてよいのかもしれません.
Re: 静電場について
mNeji さんのレス (2009/05/22(Fri) 13:43)
似た状況としては,太陽と地球との重力もそうですね.
重力も電気力も,2体の粒子間の相互作用です.ご存知の様に,2体系では,個々の座標系で考えるより,重心座標と相対座標とに分けて考えます.
したがって,相互作用ポテンシャルは,完全に相対座標にのみ依存していて,当然のこととして,どちらの粒子のポテンシャルと分けて考えることは出来ない様におもいます.
Re: 静電場について
Yokkun さんのレス (2009/05/22(Fri) 18:25)
digiさん,こんにちは.まずはa)について,参考になるかわかりませんが,議論に参加させていただきます.
>q2の電場がE(r)に影響を与えたりしないのでしょうか?
もちろん,位置  の電場は,
の電場は, 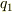 による電場と
による電場と 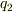 による電場の重ね合わせですから,
による電場の重ね合わせですから, 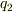 の存在が電場
の存在が電場 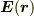 に影響を与えるのは避けることができません.すると,
に影響を与えるのは避けることができません.すると, 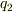 の位置に
の位置に 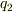 自身がつくる電場はいかに?ということになりますよね.クーロンの法則によれば,無限大に発散するともいえますし,等方性からいってゼロであるともいえます.無限大に発散しても方向が定まらなければゼロであるといわざるをえない気もします.自身が源となる場から自身が全体として有限の力を受けたらおかしなことになりますね?
自身がつくる電場はいかに?ということになりますよね.クーロンの法則によれば,無限大に発散するともいえますし,等方性からいってゼロであるともいえます.無限大に発散しても方向が定まらなければゼロであるといわざるをえない気もします.自身が源となる場から自身が全体として有限の力を受けたらおかしなことになりますね?
もともと, 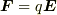 という表現において
という表現において 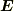 に
に  がつくる自己場は含めないというのが当然のルールにもなっています.これを「含めても自己場はゼロだから同じ」と解釈することもできるでしょう.
がつくる自己場は含めないというのが当然のルールにもなっています.これを「含めても自己場はゼロだから同じ」と解釈することもできるでしょう.
一方,徹底した近接作用論に立てば,電荷による空間の電気的なひずみ(すなわち電場)が電荷に電気力という作用をおよぼすと考えることができます.ファラデーにあっては電気力線の性質,マクスウェルにあってはマクスウェルの応力がその幾何学的・数学的な表現ということになると思います.このとき,複数の電荷がある場合にそれらがつくる電場の重ね合わせの結果として生じる,正真正銘の(自己場を含む)空間の電気的なひずみから計算される応力の積分という形で,電気力が導かれることになります.イメージとしては,力線というゴムひもに引かれる電荷…というところでしょうか.そのゴムひもの曲がりに対して,力を受ける電荷も寄与しているのは当然のことです.したがって,マクスウェルの応力に登場する 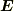 は,重ね合わせの結果としての
は,重ね合わせの結果としての 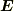 を意味しています.
を意味しています.
Re: 静電場について
digi さんのレス (2009/05/24(Sun) 07:04)
回答ありがとうございます.
(a)
>もともと, 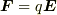 という表現において
という表現において 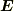 に
に  がつくる自己場は含めないというのが当然のルールにもなっています.これを「含めても自己場はゼロだから同じ」と解釈することもできるでしょう.
がつくる自己場は含めないというのが当然のルールにもなっています.これを「含めても自己場はゼロだから同じ」と解釈することもできるでしょう.
たしかに,当然のルールとなっていますね. 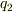 を運んでくるときには
を運んでくるときには 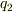 による電場の変化もあるが,
による電場の変化もあるが, 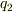 の電場
の電場 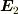 は
は 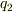 には影響しない?
には影響しない? 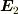 は
は 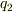 に仕事をしない?つまり,自己場はゼロ.とみてよいということでしょうか?
に仕事をしない?つまり,自己場はゼロ.とみてよいということでしょうか?
点電荷の 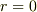 のところは電場はどうなっているかはわかるのでしょうか?
のところは電場はどうなっているかはわかるのでしょうか? 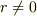 では
では 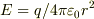 でしょうから,限りなく点電荷に近ければ無限大といえますよね.でも
でしょうから,限りなく点電荷に近ければ無限大といえますよね.でも 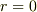 だと,Yokkunさんがおっしゃるようにどうなっているともいえないのでしょうか?
だと,Yokkunさんがおっしゃるようにどうなっているともいえないのでしょうか?
(b)ポテンシャルは2個の電荷の間に生まれるから,片方ずつでポテンシャルについて言及するのはおかしいということですね.そんな気がします.でも,「 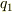 が
が 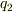 に対してポテンシャル
に対してポテンシャル  をもつ」という言い方をすれば,逆に「
をもつ」という言い方をすれば,逆に「 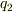 が
が 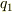 に対してポテンシャル
に対してポテンシャル  をもつ」もできますよね.この言い方自体はどちらもあっているとしていいわけですね?ポテンシャルというのは一種のエネルギーだと思いますが,それなら全体のポテンシャルは各電荷のポテンシャルの和になるのでは?(くどい感じで申し訳ありません,自分も電荷がペアで1つのポテンシャルを持つことはわかったのですが,このような考え方もあるのでは思いまして)
をもつ」もできますよね.この言い方自体はどちらもあっているとしていいわけですね?ポテンシャルというのは一種のエネルギーだと思いますが,それなら全体のポテンシャルは各電荷のポテンシャルの和になるのでは?(くどい感じで申し訳ありません,自分も電荷がペアで1つのポテンシャルを持つことはわかったのですが,このような考え方もあるのでは思いまして)
すみませんが,電気双極子のエネルギーの導出についてもわからないので質問してもよろしいでしょうか?
(c)電場 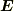 中にある,双極子モーメント
中にある,双極子モーメント 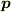 の電気双極子の静電ポテンシャルは
の電気双極子の静電ポテンシャルは 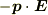 とあらわされる.この導出について,参考書では「
とあらわされる.この導出について,参考書では「 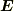 による電位を
による電位を 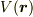 ,双極子モーメントを
,双極子モーメントを 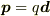 ,双極子の中心の位置を
,双極子の中心の位置を 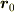 ,両端の電荷
,両端の電荷 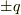 の位置を
の位置を 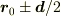 として,静電ポテンシャルは
として,静電ポテンシャルは 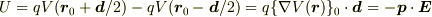 」としています.
」としています.
式変形では,静電ポテンシャルには外部電場 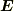 しか考慮されてないような気がしますが,
しか考慮されてないような気がしますが, 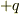 の電荷のところの電場は,自己場はないとしても
の電荷のところの電場は,自己場はないとしても 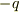 による電場があるはずでは?だから,
による電場があるはずでは?だから, 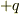 と
と 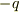 の電荷がもつ静電ポテンシャル
の電荷がもつ静電ポテンシャル 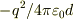 はいらないのでしょうか?
はいらないのでしょうか?
それから,最後から2つめのイコールはどういう変形でしょうか? 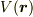 については具体的な式を考えての変形でしょうか?それともTaylor展開して近似しているのでしょうか?
については具体的な式を考えての変形でしょうか?それともTaylor展開して近似しているのでしょうか?
Re: 静電場について
mNeji さんのレス (2009/05/24(Sun) 11:26)
b)については,電子-電子のような場合を想定してみました.でも,バルクな部分1と部分2については,両者の間の静電力が,相互に作用・反作用をみたしていればいいだけで,どこにポテンシャル・エナジを振り当てるかは,考え易いようにすれば良いのではないでしょうか.
a)の自己エナジについては,電子-陽子の系で,収縮が起こったというような事がないので,「そんなに深刻な問題なのだろうか?」と感じています.ただ,もし論議するなら,「点電荷仮説」をどう捉えるかが問題かと思います.
何れにしろ,私はこれらの問題を深く考える能力がないので,これにてコメントを終了させて頂きます.
Re: 静電場について
Yokkun さんのレス (2009/05/24(Sun) 22:18)
a)について
現実の問題として点電荷において 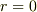 の自己場を考えることは,たとえば電子の中心でどうなっているかというような問題になり,古典電磁気学の領分ではないように思います.古典的,純粋数学的には,点電荷そのものの場所は場の湧き出しあるいは吸い込みに当たるわけですから,電場は定義できないというのが正しいような気もします.当然のように,点電荷に十分近づいた所では電場は球対称で等方的になり,微小な球面上でのベクトル和がゼロに収束することはいえるわけで,自己場によって自分が力を受けるなどという原理的破綻は免れると思います.
の自己場を考えることは,たとえば電子の中心でどうなっているかというような問題になり,古典電磁気学の領分ではないように思います.古典的,純粋数学的には,点電荷そのものの場所は場の湧き出しあるいは吸い込みに当たるわけですから,電場は定義できないというのが正しいような気もします.当然のように,点電荷に十分近づいた所では電場は球対称で等方的になり,微小な球面上でのベクトル和がゼロに収束することはいえるわけで,自己場によって自分が力を受けるなどという原理的破綻は免れると思います.
b)について(ちょっと余談になります)
たとえば,ばねにつながれた物体の弾性力による位置エネルギーという初歩的な位置エネルギーの概念においてすでに,「物体がもつエネルギー」と「場がもつエネルギー」との2つの考え方が共存しています.たとえば,縮んだばねにつながれた物体は,ばねに押される仕事をされることによって運動エネルギーを獲得し,他の物体に衝突するなどして「仕事をする能力」をもつ.したがって,縮んだばねにつながれた物体は位置エネルギーをもつということができます.一方,エネルギーはばねの中に弾性エネルギーとして蓄積されているという考え方もありますね?後者は,「場がもつエネルギー」という考え方につながるように思います.
同様に,複数の質量の間の万有引力や,複数の電荷の間の静電気力についても,質量や電荷をもつ「物体がもつ位置エネルギー」という見方と重力場や電場が存在する空間すなわち「場がエネルギーを蓄えている」という2つの見方が可能なのだと思います.前者の場合,一方を固定しない限り両者が仕事をされますから,位置エネルギーは物体の集合=系がもつと考える必要があります.
いずれの考え方も場合によって認められていいのですが,究極的には電磁波のエネルギーなどに言及が発展することになれば,「場がもつエネルギー」がまさに実体をもつことになり,「物体がもつ位置エネルギー」という初歩的な概念の限界が見えることになるのだろうと思います.
c)について
双極子の正負の電荷の相対距離はひとまず固定されているというのが前提でしょうから,内部にもつポテンシャルエネルギーは,双極子場を考える時点では考慮しなくてよい(外に取り出されることがない)ということでしょうか.ばねが伸びた状態で2つの物体につながれているが,ばねとは別に固定した長さの棒でもつながれているというようなものです.ばねは伸びたまま固定されており,その弾性エネルギーは外部と収支を得ることができないわけです.
双極子の構成電荷の相対距離変化を考慮するような場合には,その内部のポテンシャルが当然顔を出すことになると思います.
式変形について >Taylor展開して近似 が当たっているんじゃないでしょうか?
Re: 静電場について
digi さんのレス (2009/05/26(Tue) 21:56)
a), b)については厳密に考えるにはかなりの知識が必要みたいなので,自己場がその電荷自身に影響を与えることはない,ポテンシャルエネルギーは電荷の組が系として持つエネルギーと考えることにします.
みなさんのお話を聞いてとても参考になりました.ありがとうございました.
c)なのですが,2つの電荷間は棒でつながれているという過程がありました.わたしの勉強不足でした.でも,ばねが棒に変わったのならポテンシャルはないと思いますが,電荷なら間が棒でもポテンシャルがあるように思うですが?
あと,このポテンシャルはマイナスの符号が付いていますが,これはどういう事情でしょうか?電場とダイポールの向きがそろったほうがエネルギーが低いというのは予想できますが,マイナスがついているというのはいまいちわかりません.教えていただけないでしょうか.
Re: 静電場について
Yokkun さんのレス (2009/05/27(Wed) 00:27)
>ばねが棒に変わったのならポテンシャルはないと思いますが,電荷なら間が棒でもポテンシャルがあるように思うですが?
ばねが棒に変わったというのでなく,両方あるとしたのです.ポテンシャルエネルギーはあっても,とりだせないという意味でたとえとしました.なお,問題で問われているのは,外部電場の中におかれた双極子の位置エネルギーの意味ですね.ですから,「系がもつポテンシャルエネルギー」というときの「系」は,この場合厳密には外部電場(またはその源である固定電荷)を含んでいます.
>マイナスがついているというのはいまいちわかりません.
これは単に,電位と電場の関係
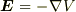 によるものです.電場は電位の坂を「下る」方向なのですね.
によるものです.電場は電位の坂を「下る」方向なのですね.
Re: 静電場について
digi さんのレス (2009/06/04(Thu) 17:55)
返事が遅れて申し訳ありません. みなさんのお話を聞けてよかったです. ありがとうございました!
Re: 静電場について
anon さんのレス (2009/06/04(Thu) 20:06)
- について.
空間に二つの電荷q1とq2があるとき,q2はq1から力を受けます. この現象をどうとらえるかについて,次の二つのとらえ方があります. ひとつは,q1とq2の相互作用だととらえるもの. もうひとつが,電場を介するものです.
電場を介したとらえ方は,以下のようなものです. (1) まず,空間にq1だけが存在している状態で空間そのものが変質して電場が発生する. このとき発生する電場はq1だけに依存するもので,q2が存在するかしないか, q2がどこに存在するかなどとはまったく無関係に,q1が空間に引き起こすものと考えます. (2) 電場の存在する空間にq2が置かれると,q2は電場によって力を受ける. この力は,q2を置く前から現にその空間にあった電場にのみよっていて, その電場が何によって引き起こされたものなのかということはまったく関係がありません. このとらえ方をするときにq2が受ける力は, 空間にq2が置かれる前からそこにあった電場によるので, その電場がq2の位置によって影響を受けたりすると考えることはできません.
仮にq1,q2以外にq3という電荷がある場合は,q3に力を及ぼす電場は, q3が置かれる前にそこにq1とq2が作っていたはずの電場であるわけなので, 当然その電場にはq2の位置が影響します.
ですから,静電気力を電場を介して理解する前提として, “自己の作る電場”という概念自体がそもそもおかしいのだと思います.