赤方偏移
赤方偏移
ファイル さんの書込 (2009/05/21(Thu) 19:52)
シュヴァルツシルト計量での赤方偏移のところで
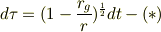
という式が出てきます.これを自分なりに解釈してみたのですが,釈然としないので,質問させてください.
自分の解釈です.
「ある点 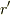 」において,静止している観測を考えます.
(つまり,
」において,静止している観測を考えます.
(つまり, 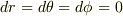 )
そのとき,局所慣性系では,計量はミンコフスキー計量なので,
)
そのとき,局所慣性系では,計量はミンコフスキー計量なので,
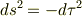
となります. 一方,同じ点において,シュバルツシルト計量は
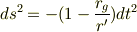
です. 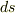 はスカラーで座標系に依らないですから,
はスカラーで座標系に依らないですから,
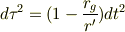
が得られ,一番上の式になるのであると思います.
つまり,これは,点 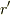 においての式だと思うのですが,
佐藤勝彦氏の教科書をみると
「動径rに一つの時計を固定して置く.この時計の進む時間,つまり固有時
においての式だと思うのですが,
佐藤勝彦氏の教科書をみると
「動径rに一つの時計を固定して置く.この時計の進む時間,つまり固有時  は
は 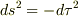 であるので,(*)が得られる.
この座標系は無限遠方で漸近的にミンコフスキー時空に近づく座標系であるので,
であるので,(*)が得られる.
この座標系は無限遠方で漸近的にミンコフスキー時空に近づく座標系であるので, 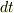 は無限遠方で静止している観測者の固有時間である.」
と書いてあります.
これだと,(*)式の左辺と右辺で,観測者の場所が異なるような解釈なのですが,
は無限遠方で静止している観測者の固有時間である.」
と書いてあります.
これだと,(*)式の左辺と右辺で,観測者の場所が異なるような解釈なのですが, 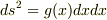 は座標系には依らないけれども,場所によって変化する量なので,同じ場所で比べなければならないのでないのでしょうか?
は座標系には依らないけれども,場所によって変化する量なので,同じ場所で比べなければならないのでないのでしょうか?
Re: 赤方偏移
Yokkun さんのレス (2009/05/22(Fri) 22:08)
ファイルさん,こんばんは.
座標系の乗り換えは,分かったようでなかなか難しいものだと常々思います.
まず,角変位は無視するとしてシュバルツシルト計量は
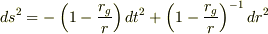 ですが,
ですが, 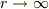 の極限をとればわかるように,そもそも重力源の無限遠方で平坦なミンコフスキー時空に一致するようにとられた座標計量であることが前提されています.つまり,無限遠から見て重力源から平坦な時空が続いていると仮定して換算した半径
の極限をとればわかるように,そもそも重力源の無限遠方で平坦なミンコフスキー時空に一致するようにとられた座標計量であることが前提されています.つまり,無限遠から見て重力源から平坦な時空が続いていると仮定して換算した半径  の位置に固定した時計の刻みが,手元の(無限遠の)時計の刻み
の位置に固定した時計の刻みが,手元の(無限遠の)時計の刻み 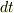 に対して
に対して
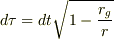 と観測されることになると思います.
と観測されることになると思います.
もともと,シュバルツシルト計量の座標 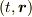 は位置
は位置  に静止した系から見た座標でもなければ,同じ位置にある局所慣性系の座標でもないと思います.その辺に混乱があるような気がするのですが….
に静止した系から見た座標でもなければ,同じ位置にある局所慣性系の座標でもないと思います.その辺に混乱があるような気がするのですが….
Re: 赤方偏移
ファイル さんのレス (2009/05/25(Mon) 22:28)
こんばんは. 返信が遅くなり,申し訳ありません.
Yokkunさんの,
>手元の(無限遠の)時計の刻み 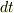 に対して
の部分,「無限遠の」と限定する必要はないように思うのですが・・・.
に対して
の部分,「無限遠の」と限定する必要はないように思うのですが・・・.
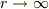 のときに,
のときに, 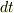 は固有時間に一致する,というだけで,
は固有時間に一致する,というだけで, 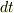 自体は,どの位置rにおいて考えても問題ないように思います.
自体は,どの位置rにおいて考えても問題ないように思います.
つまり,私は(*)の式を,ある一点(もちろん,その点は任意ですが)での,局所慣性系(左辺)と一般座標系(右辺)の関係式ではないかと考えているのですが・・・.
例えば, 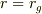 では
では
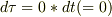 になり,
になり,
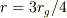 では
では
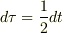 もちろん,
もちろん, 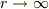 では
では
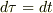 になります.
になります.
いろいろ検索してみたところ,ある質問サイトで似たような質問をしている方がおり,そこに私の考えと同じではないか?というような教科書の画像があったので,
よろしかったら,見てみてください.私の説明は下手ですが,上で行われている計算と同じことを言いたいんです.(転載がまずかったらおっしゃってください.すぐに,削除します.江里口良治氏の本だそうです.)
Re: 赤方偏移
ミュフ猫 さんのレス (2009/05/26(Tue) 07:51)
ファイルさん,こんにちは.
私もそこを疑問に思っています. アインシュタイン方程式の解からシュバルツシルト計量を導出する際, 初期条件として, 「無限遠でミンコフスキー時空に一致」 を用いているので,この場合の座標時間dtが無限遠で静止する観測者の固有時間 に等しいことは,理解できます. 問題は,位置rに静止する観測者が無限遠で静止状態にある物体の固有時間を,
(1-rg/r)^(-1/2) −(※)
の時間比で速く感じるか否かです. もし,そう感じるなら結果的に,dt自体はどの位置rにおいて考えても問題ない ように思います. ところが,その事を厳密に証明するためには,初期条件として, 「位置rで局所的に向心方向の一様重力場g(r)に一致」 を用いて,アインシュタイン方程式の解を導出し,位置rに静止する観測者の 固有時間となる座標時間dtと,無限遠で静止状態にある物体の固有時間との 時間比が,(※)に一致することを示さねばならないのではないでしょうか.
ちなみに,位置rで静止し続ける観測者と位置rで瞬間的に静止する自由落下物体 との固有時間は,重なる瞬間には同期すると思います. つまり,位置と速度が一致する瞬間,加速度の違いにかかわらず, 互いの固有時間を共有できるのではないでしょうか.
Re: 赤方偏移
Yokkun さんのレス (2009/05/27(Wed) 00:06)
ファイルさん,ミュフ猫さん,こんばんは.
【ファイルさん】 >私は(*)の式を,ある一点(もちろん,その点は任意ですが)での,局所慣性系(左辺)と一般座標系(右辺)の関係式ではないかと考えているのですが・・・.
その通りだと思います.そして,このことは
【ミュフ猫さん】 >ちなみに,位置rで静止し続ける観測者と位置rで瞬間的に静止する自由落下物体 との固有時間は,重なる瞬間には同期すると思います.
につながることだと思いました.ミュフ猫さんの前段の話は,その意味がまだよく飲み込めていないので保留させていただきますが,上の点は重要なことで,局所慣性系がいわば曲がった時空の接平面であるということに通じるものだと思います.シュバルツシルト座標系から見て特定された位置において両者が計量を同じくするということですよね?
さて,そもそもの疑問は「赤方偏移」の議論から発したとのことですので,私のつたない理解を吐露しようと思いましたが,どうにもまとまらず…とりあえず書籍からの引用をして議論の参考にさせてください.ちょっと長いですが…
「2つの事象として,ブラックホールの近くの球殻で静止している時計の刻む音を選ぶ.静止するということは事象間の空間間隔が0であることを意味する: 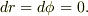 (座標系の同じ場所で起きる事象間の時間として定義される)固有時
(座標系の同じ場所で起きる事象間の時間として定義される)固有時 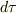 は球殻時計で読まれる
は球殻時計で読まれる 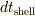 である.シュワルツシルト計量を使うと,球殻時計の経過時間と遠方時計の経過時間の関係がわかる:
である.シュワルツシルト計量を使うと,球殻時計の経過時間と遠方時計の経過時間の関係がわかる:
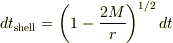 この式を評価するとき,時計の刻む音の代わりに,
この式を評価するとき,時計の刻む音の代わりに,  の球殻から外側に放出される定常波の周期を使うことができる.遠くの観測者が測定する周期
の球殻から外側に放出される定常波の周期を使うことができる.遠くの観測者が測定する周期 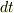 は,発信する時計のところで測定する周期
は,発信する時計のところで測定する周期 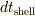 よりも大きくなる.長い周期の可視光は赤い光である.そのため,この効果の一般的な名称を重力赤方偏移とする.」(「一般相対性理論入門―ブラックホール探査」テイラー,ホイーラー著牧野伸義訳)
よりも大きくなる.長い周期の可視光は赤い光である.そのため,この効果の一般的な名称を重力赤方偏移とする.」(「一般相対性理論入門―ブラックホール探査」テイラー,ホイーラー著牧野伸義訳)
「定常波」というのがわかりませんが,赤方偏移した光の観測はまさに  に固定した時計の刻みを
に固定した時計の刻みを 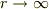 において観測したに等しいということをいっているようです.そして上の式は,ファイルさんの(*)とミュフ猫さんの「同期」によって説明することができると思います.
において観測したに等しいということをいっているようです.そして上の式は,ファイルさんの(*)とミュフ猫さんの「同期」によって説明することができると思います.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/05/27(Wed) 07:39)
Yokkunさん,返信ありがとうございます.
私もよく解っていませんので,読み流してください.w ただ,位置rに静止する観測者と,無限遠で静止する観測者との両者間で, 「同時の破れ」が生じているか否かを検証するのに,シュバルツシルト計量 のみでは不十分な気がしてます. 互いに同時刻空間を共有していれば,例えば,位置rから無限遠への送信で, 時間比が半分になる赤方偏移が生じるとき,無限遠から位置rへの送信に対し, 時間比が2倍になる青方偏移が生じると言えると思います. ところが,「同時の破れ」によって同時刻空間が共有されていなければ, 半分の赤方偏移に対して,青方偏移が厳密に「2倍」とは言い切れない ような感じがしてます.
Re: 赤方偏移
Yokkun さんのレス (2009/05/27(Wed) 12:05)
比較しているのはあくまで
- rに静止した原子が発する光の周期をrに静止した観測者(球殻系)が手元の時計で測定した値(dτ)
- rに静止した原子が発する光の周期を無限遠に静止した観測者が手元の時計で測定した値(dt)
の2つであるということだと思います.そうすると,同じ位置rに静止した(dr=0)2事象間の時間測定を異なる場所で行った結果の比較ということになり,おっしゃるような矛盾は生じないのではないでしょうか?測定する時計の場所は違いますが,測定対象である2事象は同じ位置rでなおかつ静止(dr=0)が保たれた同一のものなのです.
結果的に必要なのは,
観測される光の振動数(周期)に影響するのは時空の「形」のみであること
だと思いますが,これは相対論の母たる電磁気学で保証されているものと考えたいのですが,いかがでしょうか?そして時空の曲がり具合が2人の観測者の位置を含む広域的なものとして与えられている(シュワルツシルト計量)のですから,これら2つの測定を比較することはもちろん可能であると思います.
Re: 赤方偏移
ファイル さんのレス (2009/05/28(Thu) 01:01)
>ミュフ猫さん こんばんは.「同時の破れ」については,少し私には難しくてよく分からないです.すみません. ところで, >重なる瞬間には同期すると思います. の「重なる」というのはどういうことですか?
>Yokkunさん 「赤方偏移」というタイトルをつけたのが,あまり良くなかったのかもしれません. 私が知りたいのは赤方偏移のことよりも,むしろ
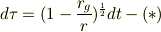
の数学的な導出についてです. もっといえば,シュバルツシルト時空でなくても一般的に
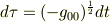
でも構わないです.
赤方偏移というタイトルをつけたのは,大抵,(*)の式が出てくるのが赤方偏移の話題のところなので,そうしたのですが,Yokkunさんが引用された本
>シュワルツシルト計量を使うと,球殻時計の経過時間と遠方時計の経過時間の関係がわかる
のように,ほとんどの本では,あまり詳しい計算の導出が書いておらず,物理的な現象の説明だけで終わっています.
そこで,私は,(*)式を「ある一点において,計量テンソルをミンコフスキー計量になるように座標変換し,それを一般座標における計量と等しいとする」ことによって導いたわけですが,そのように計算すると式は正しく導かれるが,多くの本に載っている説明「遠くの観測者が測定する周期 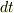 」の部分が少しおかしく感じてしまうのです.
」の部分が少しおかしく感じてしまうのです.
ですから,私の気持ちとしては,ブラックホールの球殻で静止している時計の音と,一般座標系の同じ位置(=ブラックホールの球殻)で静止している時計の音を比べたいわけですが これを実際に観測しようとすると,「一般座標系の同じ位置(=ブラックホールの球殻)で静止している時計の音」=その位置での光を無限遠から見た人の時計 ということになるのですかね・・・? ちょっとここら辺の理解がイマイチあやふやというか,納得できないのですが,数学的な計算と,実際にどうやって観測するのか,というギャップが原因なのでしょうか・・・.
Re: 赤方偏移
ファイル さんのレス (2009/05/28(Thu) 01:16)
上の記事は,愚痴をだらだらと書いたもののようになってしまったのですが
要するに,多くの本に書かれている観測的説明(No.23888の記事でいえば「シュワルツシルト計量を使うと,球殻時計の経過時間と遠方時計の経過時間の関係がわかる」の部分)をなんとか数式だけで表現したいんです.
固有時間であるものを 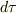 ,どの位置で考えているかについては添え字で表現します.
,どの位置で考えているかについては添え字で表現します.
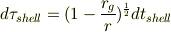
は,No.23869のリンク先の計算から導出できます.
また, 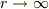 において
において
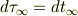
です.もし,
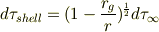
となれば,本の説明が納得できるのですけれど,計算で示すことができません.
おそらく,私が悩んでいるところがお二人が議論されている内容より,もっと低レベルな部分だと思います.根本的なところがよく分かっていないのかもしれません.
Re: 赤方偏移
佐藤 さんのレス (2009/05/28(Thu) 11:06)
佐藤と申します.
横からすいません. よくわかっていませんが,コメントをば.
もし………となれば納得すると書かれていますが, そうはならないと思います.
あくまで同じ点での座標変換なのではないでしょうか?
ただ"t"の物理的意味が無限遠でMinkowskiとなっている観測者の"t"だということではないでしょうか? 別に無限遠から見てるわけではないじゃないですか?
Re: 赤方偏移
ミュフ猫 さんのレス (2009/05/28(Thu) 13:30)
Yokkunさん,返信ありがとうございます.
>(1) rに静止した原子が発する光の周期をrに静止した観測者(球殻系)が手元の時計で測定した値(dτ) >(2) rに静止した原子が発する光の周期を無限遠に静止した観測者が手元の時計で測定した値(dt)
dτとdtが上記で定義される時間ならば,矛盾は生じないと思います. 私が言いたかったのは,
(3)無限遠に静止した原子が発する光の周期をrに静止した観測者(球殻系)が手元の時計で測定した値(dt') (4)無限遠に静止した原子が発する光の周期を無限遠に静止した観測者が手元の時計で測定した値(dτ')
と言うように,dt'とdτ'を定義しても,
dτ'/dt' = (1-rg/r)^(-1/2)−(※)
が成り立つか否かをシュバルツシルト計量のみから判別することはできないのでは? と言うことです. そして,もし,アインシュタイン方程式から(※)を導出できれば, 位置rに静止する観測者と,無限遠で静止する観測者との両者間で, 「同時の破れ」は生じておらず,同時刻空間を共有していることが 示されるのではないかと思っています.
ややこしくしてしまって,すいません.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/05/28(Thu) 13:38)
ファイルさん,返信ありがとうございます.
>「重なる」というのはどういうことですか?
位置rで静止し続ける観測者と位置rで瞬間的に静止する自由落下物体が, 互いの位置と速度を共有すると言う意味です.
Re: 赤方偏移
ファイル さんのレス (2009/05/29(Fri) 00:26)
>佐藤さん >ただ"t"の物理的意味が無限遠でMinkowskiとなっている観測者の"t"だということではないでしょうか? シュバルツシルト計量の座標系が,そのようなものに限定されてしまっている,ということでしょうか? 一般相対論においては,どんな座標系でも選ぶことが出来,さらに,(*)式の右辺は一般座標系での表現なので「tはどんな座標系のtでも良いのだ」と勝手に考えていたのですが,ミュフ猫さんもおっしゃっていたように,初期条件として「無限遠でミンコフスキー時空に一致」を課した時点で,座標系を選択する自由度?は失われてしまったのでしょうか.
つまり,時空に「無限遠でミンコフスキー時空になるような座標t」を張り巡らせるようなイメージでしょうか. 確かに,そう考えると,(*)式が一点において成り立つ式だという私の考えと,多くの本に書いてある説明とは矛盾しませんね.
>ミュフ猫さん ご回答ありがとうございます.
Re: 赤方偏移
Yokkun さんのレス (2009/05/29(Fri) 21:57)
みなさん,こんばんは.
【ミュフ猫さん】>私が言いたかったのは,(3)・・・
「前段の話は,その意味がまだよく飲み込めていないので保留させていただきますが,」というわけでした.
【ファイルさん】>シュバルツシルト計量の座標系が,そのようなものに限定されてしまっている,・・・
その通りだと思います.シュバルツシルト計量は広域的な時空の計量を与えていますが,その時間座標は無限遠の固有時に一致するように,そして動径座標は円周が2πrになるように換算されている「特化」した座標なのではないでしょうか.
【ファイルさん】>つまり,時空に「無限遠でミンコフスキー時空になるような座標t」を張り巡らせるようなイメージでしょうか.
まさにこの表現がぴったりくると思います.計量は指定された2事象間の時空距離(インタバル)を与えますが,佐藤さんもふれておられるように実は観測者の位置は特定されていなくてもよいのです.実際の観測について思考実験するなら,シュバルツシルト計量の特化された座標を目的の観測系に必要に応じて変換すればそれですみます.そして観測系は球殻系など局所的なものでもよいのだと思います.その位置の局所慣性系と観測系の変換がわかっていればよいわけです.
これは,そもそも曲がった空間を平坦な微小空間の貼りあわせとして表して,となりあう微小空間どうしの接続を指定することによって大域的な空間の曲がりを記述するというリーマン幾何学の基本的なアイディアによるものだと思います.つまり,シュバルツシルト計量によって広域的な時空が局所慣性系の集合として記述され,異なる時空点におけるインタバルを直接比較できるわけです.
もうひとつ考慮に入れる必要があると思われるのは,「広域的な」(?)相対性原理.どんな局所慣性系も慣性系である限り同等で,たとえば系に静止したある原子の決まった遷移によって生じる光の振動数は,すぐそばに静止した観測者が測定する限りどの系でも同じであるということです.ちなみに原子の発する光に関する限り,この振動数は球殻系のように重力があっても同じだと思います.これを,異なる位置の「同時刻空間の共有」に使えるのではないでしょうか?このとき,同じ位置の局所慣性系と球殻系の「同期」が役に立つように思われます.
※ミュフ猫さんの(※)もこれで解決!・・・と思いましたが,実はまだよくわかっていません.
Re: 赤方偏移
ファイル さんのレス (2009/05/31(Sun) 18:15)
>Yokkunさん (*)式の右辺が一般座標系と呼ばれているので,どの座標系も表しているんだ,という変な勘違いをしていたのが問題だったのですね.
勉強になりました. 皆様,ありがとうございました.
#ミュフ猫さんのおっしゃっていることは,(※)式を導くにはシュバルツシルト計量をどう座標変換しても不可能で,また別の計量(静的で球対称な)を導く必要がある,ということでしょうか.やっとなんとなく分かってきました.
Re: 赤方偏移
Yokkun さんのレス (2009/05/31(Sun) 18:55)
>…(※)式を導くにはシュバルツシルト計量をどう座標変換しても不可能で,また別の計量(静的で球対称な)を導く必要がある,ということでしょうか.
残る問題はそこなのですよね.時空の全体像はシュバルツシルト計量で与えられているので,あとは広域的な(局所的でない)球殻系との間の座標変換(球殻系による計量)が得られればよいのだと思うのです.少なくとも場の方程式までもどる必要はないと考えます.…が,スケールを変換するだけで単純だと思ったのに何か引っかかってて,「これだ」というものを示せないでいます.^^;
とりあえず,ファイルさんの疑問は解決したようですね.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/05/31(Sun) 19:57)
ファイルさん,返信ありがとうございます.
>>ミュフ猫さん >ご回答ありがとうございます.
どういたしまして.
Yokkunさん,返信ありがとうございます.
>「前段の話は,その意味がまだよく飲み込めていないので保留させていただきますが,」というわけでした.
了解しました.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/05/31(Sun) 21:23)
ちょっと,変なアイディアがあります.
ある慣性系に対して,等速で自転する観測者がもつ回転系と, 瞬間的に静止するような等加速度運動する観測者がもつ等加速度系を比較すると, 前者において,自転する観測者Aから見て常に静止しているように見えるような 運動(等速円運動)をする観測者Bは,Aに対し同時刻空間を共有しませんが, 後者において,等加速度運動する観測者Cから見て常に静止しているように見える ような運動(加速度値が同じとは限らないが,これも等加速度運動)をする 観測者Dは,Cに対し同時刻空間を共有します. これらの違いは,回転系が「時間軸に直交しない系」であるのに対し, 等加速度系が「時間軸に直交する系」であることに関係があるかもしれません. もし,そうなら,シュバルツシルト計量によって張られる座標系が, 「時間軸に直交する系」であることを用いて,(※)式を導けるかもしれません.
おもいっきり適当な推量ですが・・・.w
Re: 赤方偏移
Yokkun さんのレス (2009/05/31(Sun) 21:46)
ランダウの「場の古典論」にこの議論に関わると思われる記述があり,t=一定の超平面が時間軸に直交する「同期化された基準系」というのが出てきます.私にはとても読みきれないレベルですが.
ミュフ猫さん,おかげさまで気になる宿題がまたひとつ増えました.m__m
Re: 赤方偏移
ミュフ猫 さんのレス (2009/05/31(Sun) 22:23)
>ミュフ猫さん,おかげさまで気になる宿題がまたひとつ増えました.m__m
Yokkunさん,どういたしまして.w
ファイルさん,余計なお世話ですが,「EMANの物理学」の談話室で, この度の疑問をぶつけられてはいかがでしょうか? 有意義な回答が得られると思います. すみません.言い出しっぺの私には知識も勇気も無いので・・・.w
Re: 赤方偏移
Yokkun さんのレス (2009/06/01(Mon) 09:17)
ミュフ猫さん,「EMANの物理学」の赤方偏移の部分 > http://homepage2.nifty.com/eman/relativity/redshift.html
にある議論を適用して,位置Aを動径座標rの位置,位置Bをr=∞の位置とすれば,どちらで観測するかにかかわらず,両者の振動数の観測値の比は決まってしまい,(※)が得られるのではないかと思いました.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/06/01(Mon) 13:02)
Yokkunさん,ご指摘のURLの解説を読みました.
どうやら,その解説に書かれた考え方が私の疑問を解決するための ヒントになるかもしれませんね. しかし,このまま初期条件を当てはめるだけで解決するとは言い切れない かも知れません.というのも,
『ただしここで注意が必要なのだが,今使っている座標系というのは, 地表に対する静止系であるという事以外は特に断っておらず, どの地点にいる観察者の視点に立ったものであるかは指定していなかった. それは A の視点での座標かも知れず B の視点かも知れず, いずれでもないかも知れない.しかしそれはどう選んでも良いのだ.』
上記の引用部分についてですが,ここで言う「どう選んでも良い視点」とは, 「その視点での座標系が,
(ds)^2 = g00*(dw)^2+g33*(dz)^2
で示される計量によって張られるものならば」 と言う条件が付いていると思うからです. ですから,アインシュタイン方程式から導かれるシュバルツシルト計量以外の 計量方程式も,二点間の固有時間比がその形式によらず変化しないような g00 成分をもつことを前提とするならば,その解説の考え方をそのまま使って 解決できると思うのですが・・・.
Re: 赤方偏移
Yokkun さんのレス (2009/06/01(Mon) 14:10)
「どう選んでもよい」の意味は,計量の形式が異なるどんな座標系を使っても,その形式が
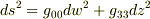 という形でありさえすれば,与えられた時空点の計量の値は同じであるから…ということだと思います.つまり,シュバルツシルト座標はこの条件に合致する座標であり,その視点が時間的には「遠方」であるということはどうでもよいと私は読み取りました.必要なのは,その定められた視点から2つの位置の固有時を比較することなのです.
という形でありさえすれば,与えられた時空点の計量の値は同じであるから…ということだと思います.つまり,シュバルツシルト座標はこの条件に合致する座標であり,その視点が時間的には「遠方」であるということはどうでもよいと私は読み取りました.必要なのは,その定められた視点から2つの位置の固有時を比較することなのです.
ランダウの本では,同期化された基準系の条件というのが
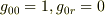 であると書いてあったと思いますが,このうち
であると書いてあったと思いますが,このうち 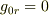 にする座標変換はいつでもできて,そのことを説明したのが「EMANの物理学」の赤方偏移の前半です.シュバルツシルト座標ではこれはもう済んでいます.また,
にする座標変換はいつでもできて,そのことを説明したのが「EMANの物理学」の赤方偏移の前半です.シュバルツシルト座標ではこれはもう済んでいます.また, 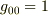 の条件は,座標を変換することで可能だと思いますが,今扱っている問題では,例えば固定された位置r=aからの視点で時空全体を記述する新たな計量は必要なく,それぞれに固定された位置の固有時を求めるだけでそれが可能であるのだと思います.
の条件は,座標を変換することで可能だと思いますが,今扱っている問題では,例えば固定された位置r=aからの視点で時空全体を記述する新たな計量は必要なく,それぞれに固定された位置の固有時を求めるだけでそれが可能であるのだと思います.
「EMANの物理学」では,赤方偏移の結果を
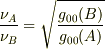 とまとめていますが,「以上の事は特にシュバルツシルト解に限らず,成り立っていることである.」といっていますね?これは,
とまとめていますが,「以上の事は特にシュバルツシルト解に限らず,成り立っていることである.」といっていますね?これは, 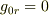 が成立して,かつ静止した観測者の場合ということであり,もちろんシュバルツシルト解でも成り立つことは当然です.
が成立して,かつ静止した観測者の場合ということであり,もちろんシュバルツシルト解でも成り立つことは当然です.
上でAとBの指定を間違えましたが,Aを無限遠,Bをrの位置としますと
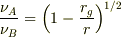 すなわちA(∞)から出た振動数
すなわちA(∞)から出た振動数 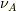 の光をB(r)に静止する観測者は
の光をB(r)に静止する観測者は
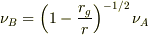 として観測することになります.
として観測することになります.
>アインシュタイン方程式から導かれるシュバルツシルト計量以外の計量方程式も,同じ g00 成分をもつことを前提とするならば,
同じ 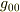 をもつ必要はなく,同じ時空の計量である限り定められた点の計量の値は変わりませんから,上で求められた比はたとえば視点をrに置いた広域的な球殻系の座標を用いても同じになる(ただし換算されたr座標は同じとして)ということではないでしょうか?計量の値を変えないが計量の形式を変えるというのが座標変換の意味ですよね.
をもつ必要はなく,同じ時空の計量である限り定められた点の計量の値は変わりませんから,上で求められた比はたとえば視点をrに置いた広域的な球殻系の座標を用いても同じになる(ただし換算されたr座標は同じとして)ということではないでしょうか?計量の値を変えないが計量の形式を変えるというのが座標変換の意味ですよね.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/06/01(Mon) 15:01)
すみません.そういうことです.舌足らずでした. 修正します. というか,修正しようとしてたとこなのに・・・. 突っ込み早すぎ.w
Re: 赤方偏移
ミュフ猫 さんのレス (2009/06/01(Mon) 15:57)
>例えば固定された位置r=aからの視点で時空全体を記述する新たな計量は >必要なく,それぞれに固定された位置の固有時を求めるだけでそれが可能 >であるのだと思います.
この部分が理解できません. 解説で述べていることを簡単に言うと,
「静的な重力場では,AからBまでの光の到達時間はどの観測者にとっても, 観測時刻に寄らず一定だよね. なら,観測者自身との固有時間比が判れば,三段論法でAとBとの固有時間比 を算出できるよね.」
と言うことでしょう? つまり,観測場所が変わっても,AとBとの固有時間比が変化しないってこと については,何も言及してないと思いますが・・・.
Re: 赤方偏移
Yokkun さんのレス (2009/06/01(Mon) 16:16)
>突っ込み早すぎ.w
ごめん,ごめん.
「EMANの物理学」の赤方偏移の「一気に解決」の部分をシュバルツシルト計量に特殊化して翻訳してみます.
さて,Aが時刻 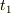 から
から 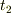 までの間,光を出し続けたとする.またBはその光を
までの間,光を出し続けたとする.またBはその光を 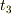 から
から 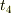 までの間,受け続けたとする.ただし,これらの時刻はシュバルツシルト時間座標とする.光の進路においては
までの間,受け続けたとする.ただし,これらの時刻はシュバルツシルト時間座標とする.光の進路においては 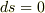 なので,
なので,
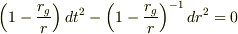 が成り立っている.よって,光の伝播に要した時間間隔は,
が成り立っている.よって,光の伝播に要した時間間隔は,
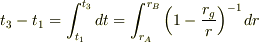 と表される.同様に,
と表される.同様に, 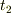 の時点でAから発射された光は
の時点でAから発射された光は 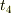 の時点でBに届くのであるから,
の時点でBに届くのであるから,
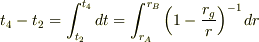 と表される.結果的に
と表される.結果的に
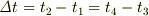 となり,Aが光を発していた時間はBが受けていた時間に等しい.ただし,
となり,Aが光を発していた時間はBが受けていた時間に等しい.ただし, 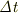 はA,Bそれぞれが観測する時間ではなく,シュバルツシルト座標時間による時間間隔である.
はA,Bそれぞれが観測する時間ではなく,シュバルツシルト座標時間による時間間隔である.
A,Bそれぞれの立場での観測時間は固有時を用いればよい.AもBも静止しているので固有時は
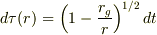 で得られる.
で得られる.
光の振動数  は,固有時
は,固有時 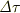 の間に,
の間に, 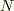 回の振動を数えたとして
回の振動を数えたとして
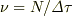
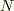 の値はAとBのどちらにとっても変わらないので,それぞれが測る振動数は
の値はAとBのどちらにとっても変わらないので,それぞれが測る振動数は
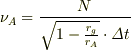
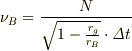 以上から,次の関係を得る.
以上から,次の関係を得る.
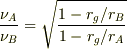 ------------------------翻訳終わり
------------------------翻訳終わり
>観測場所が変わっても,AとBとの固有時間比が変化しないってことについては,何も言及してないと思いますが・・・.
観測場所というより座標系が変わっても,あるいは「EMAN」の表現を借りれば視点が変わってもということですね.座標変換によって計量テンソルが変わってもという意味と理解しました.まず,決まった位置の固有時間は時空間隔 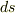 の値に等しい(かまたは比例→定義による)わけですが,その値は座標変換によって変わることの許されない量ですよね.つまり,
の値に等しい(かまたは比例→定義による)わけですが,その値は座標変換によって変わることの許されない量ですよね.つまり,
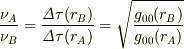 は,座標変換によって
は,座標変換によって 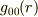 が変わってしまっても,変わることは許されない量ではないのでしょうか?
が変わってしまっても,変わることは許されない量ではないのでしょうか?
ミンコフスキー計量の値を変えない座標変換がローレンツ変換. 一般時空計量の値を変えない座標変換が一般座標変換と理解したのですが. つまり,固有時を変えない変換のみが座標変換として許されるのではないでしょうか?
Re: 赤方偏移
ミュフ猫 さんのレス (2009/06/01(Mon) 20:31)
>観測場所というより座標系が変わっても,あるいは「EMAN」の表現を借りれば >視点が変わってもということですね.
そうです.
ところで,シュバルツシルト計量をAとBとの固有時間比が変化しないように 座標変換した新たな計量方程式によって張られた座標系に対し,果たしてそれが, どの位置の観測者がもつものなのかを数学的に証明する方法が思いつきません.
また,二点間の固有時間比について,座標変換によってどのように変化しても, おかしくないと思います. 例えば,空間二次元+時間の三次元時空間で考えて見ます. 二点の世界線は時間軸に沿って延びる曲線で表されます. そして,ある観測座標系の同時刻面はそれらの世界線を切断するように 張られます. この場合,二点間の固有時間比とは,観測者にとっての単位時間に,同時刻面が 移動した領域内にある二つの世界線の線分によって各々定まる固有時間の比です. (そのままやな.w) つまり,同時刻面の張られ方,時間的な変化の仕方によって如何様にも変化し得る と単純に思ってしまうのですが・・・.
ちなみに,座標変換に対し「固有時間」が不変であるという意味は,例えば,
「寿命が百年だった人間は,どの観測者から見てもバースデーケーキに立てられた 百本のロウソクを吹き消しながら死ぬように見える.」
って事だと思います.彼の一生を一万年がかりで見続けた観測者もいれば, 一分で見終えた観測者もいます. しかし,その人間の臨終の状況に対し,すべての観測者が主張するロウソクの数 は「百」です.99や101を主張する観測者はいません. つまり,ロウソクの数こそが「固有時間」で,彼が自ら一生を通じて体感した 時の長さです.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/06/01(Mon) 21:38)
Yokkunさん,仰られている事が解って来ました.
そうか,そうか. と言うことは,ある一つの座標系で,光がAとBとの間を,双方向に同じ伝播速度 を持てば,私の疑問は解決できそうですね. つまり,ある一つの座標系において,任意の準拠点で,光の速度が等方性をもつ ならば,どんな観測点からも,AとBの固有時間比は不変になるかもしれません. 結局,「時間軸に直交する系」が座標系に一つでもあれば,いいってことなのか! つながりかけました!
Re: 赤方偏移
Yokkun さんのレス (2009/06/01(Mon) 23:40)
ミュフ猫さん,私なんかよりもずっと思考が深いです.
私などは単純に,「EMAN」の流れに乗っかって納得しただけなのですが.
ともかく,私が引っかかっていたのもつきつめれば多分ミュフ猫さんと同じ種類のものだとは思うのですが,「EMAN」にある思考実験で簡単に納得してしまいました.私の引っ掛かりをとりのぞいてくれたのは,発信側(A)と受信側(B)で光の観測時間が座標時間において等しいということです.そして,このことが 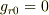 とA,Bともに座標系において静止していることのみを条件としていて,シュバルツシルトのみならず一般座標計量において成立するという点です.また,以上のことが光の世界線の時空間隔がつねにゼロ(局所的な光速不変)という,より基本的なことから導出されていることに思わず合点がいってしまいました.上の条件のもとで,固有時間が計量に関わらず一定であることはむしろ座標変換を限定する要請なのではないかと思います.
とA,Bともに座標系において静止していることのみを条件としていて,シュバルツシルトのみならず一般座標計量において成立するという点です.また,以上のことが光の世界線の時空間隔がつねにゼロ(局所的な光速不変)という,より基本的なことから導出されていることに思わず合点がいってしまいました.上の条件のもとで,固有時間が計量に関わらず一定であることはむしろ座標変換を限定する要請なのではないかと思います.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/06/02(Tue) 21:44)
今日は朝から用事で,やっと帰ってきました. Yokkunさん,返信遅れてすみません.
>私なんかよりもずっと思考が深いです.
とんでもない.私の思考など児戯レベルです.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/06/02(Tue) 22:48)
>固有時間が計量に関わらず一定であることはむしろ座標変換を限定する >要請なのではないかと思います.
私もそう思います.ちょっと,考えたのですが,以下のようにまとまると, うれしいのですが・・・.
「静的な重力場における一般の計量,すなわち,すべての成分が空間座標のみの 関数で表される計量によって張られる座標系に対し,その準拠点を観測点(視点) とする座標系への変換では,必ず,任意の二定点間(重力場に対して静止した二点間) の固有時間比が不変となる. 特に,静的な重力場において,そのままで空間の幾何を表している計量,すなわち,
g01=g02=g03=0 ,かつ その他の成分がいずれも空間座標のみの関数
で表される計量によって張られる座標系(時間軸に直交する系)に対し, その準拠点を観測点(視点)とする座標系への変換では,必ず,同時刻空間を共有する.」
見当はずれかも知れません.w
Re: 赤方偏移
Yokkun さんのレス (2009/06/02(Tue) 23:01)
ミュフ猫さん,さすがです.
厳密性を失うことなく,必要十分な要件をコンパクトにまとめていただいたと思います.静的な時空の条件はともかく,計量テンソルに時間座標を含む一般化までは思いもよりませんでした.ミュフ猫さんの悩みの意味がようやくわかった気がしました.勉強になりました.
Re: 赤方偏移
ミュフ猫 さんのレス (2009/06/02(Tue) 23:24)
Yokkunさん,お褒めいただき,ありがとうございます.
私は「EMAN」の解説を読んで,表面だけを理解してました. Yokkunさんの鋭い正確な解釈を教えていただいて,目からウロコが落ちました. そういう深い意味が隠れていたんですねぇ. こちらこそ,とても勉強になりました. 長い間いろいろ,お付き合いいただいて,本当にありがとうございました.m(_ _)m