数学迷い人 さんの書込 (2009/05/18(Mon) 12:43)

毎度すみません．自分の無知さに遺憾ですが，

ベクトル解析に平行して，電磁気学も現在学んでいます．

式の一部なのですが，

以下の式で，領域の広がりを0にする極限，ΔV→0を考えたとき，

?ρ*ΔV＝∫ρdVと出てきたのですが，どのように解釈すればよろしいでしょうか？ 公式としてもよいでしょうか？

数学迷い人 さんのレス (2009/05/18(Mon) 12:44)

自分なりに解釈したのですが，微小にすることによって，連続性を持たせているからなのでしょうか？

Yokkun さんのレス (2009/05/18(Mon) 21:54)

>微小にすることによって，連続性を持たせているからなのでしょうか？

イメージとしてはよろしいのではないでしょうか． 定積分の定義として，和による定義というのがあります．

• http://w3e.kanazawa-it.ac.jp/math/category/sekibun/henkan-tex.cgi?size=3&target=/math/category/sekibun/teisekibun-no-teigi-2.html

>?ρ*ΔV＝∫ρdVと出てきたのですが,

ほとんど定義といっていいのではないでしょうか．

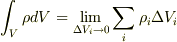
インテグラルはそもそもΣと同じ文字らしいです．

数学迷い人 さんのレス (2009/05/19(Tue) 10:46)

たしかに，それぞれの式の意味を考えてみると，同じですね． さまざまな表記ができて数学ってすごいなと思いました．

ありがとうございました．

はる さんのレス (2009/05/19(Tue) 17:23)

横レスですが，気になったのでちょっと発言します． >>微小にすることによって，連続性を持たせているからなのでしょうか？ 連続性という言葉をどういう意味で使っているかによりますが，いわゆる，微積分可能な前提条件としての連続性という意味で用いているのでしたら，連続性は初めに与えられるべき条件ですので，考えている対象が連続性があるものなら微小にしても連続性がありますし，対象が連続でなければ微小にしても連続性はでてきません． 数学迷い人さんが質問されている場合のＶに関しては，一塊の空間でしょうから，元より微積分的な意味での連続性はあると考えていいでしょう．

それで，本題 >>領域の広がりを0にする極限，ΔV→0を考えたとき， >>?ρ*ΔV＝∫ρdV・・・・・・・【Ｔ】 についてですが， Yokkunさんのリンク紹介で問題ないと思いますが，補足しておきます． 積分のイメージとしては，Yokkunさんのレスの下から２行目の数式と対応するグラフのイメージが適当であり，ライプニッツの頃などはそのように概念形成されていったらしいです．

ところが，厳密な積分の定義，すなわち【Ｔ】の原理(証明)は，その下から２行目の数式ではなく，紹介されてるリンク先の説明くらいは必要なのですが，その全文をあえて簡略に説明すれば，以下のような意味になります． 青い領域Δｘiを，Δｘi内でｆが最大になるよう伸ばした場合と，最小になるよう縮めた場合の２通り作ります．つまり図の場合は，左端ｘi-1と曲線の交点に伸ばしたもの，右端ｘiと曲線の交点まで縮めたもの，の２つです． その時の棒の頭のｙの値を，それぞれ”ｆｘi(上限)”，”ｆｘi(下限)”と名づけます． すると， ?ｆｘi(上限)*Δｘi＞?ｆｘi(下限)*Δｘi になるのはわかりますよね．もっというと， ?ｆｘi(上限)*Δｘi＞?ｆｘi(ξ)*Δｘi＞?ｆｘi(下限)*Δｘi・・【Ｂ】 です． Δをもっと細分していけば， 【Ｂ】の３つの値の差は縮まっていきます(連続ならば)． そして， ?ｆｘi(上限)*Δｘi＝?ｆｘi(ξ)*Δｘi＝?ｆｘi(下限)*Δｘi となったとき，『f(x)は[a,b]で積分可能』と判定され，ここで，初めてインテグラルの式とイコールで結ばれます．

先に言いましたが，細分すれば連続になって積分可能になるわけではありませんのであしからず．

はる さんのレス (2009/05/19(Tue) 21:15)

上のNo.23801，訂正です（キー無しで修正できないです．次から気をつけます．）

>>Ｖに関しては，一塊の空間でしょうから，元より微積分的な意味での連続性はある >>と考えていいでしょう．

連続性に関係あるのはＶというより非積分関数でした．上の個所は無かった事にしてください．

（あと，もし他にも変な間違いありましたらご指摘おねがいします．）