計算問題
計算問題
数学迷い人 さんの書込 (2009/05/11(Mon) 11:08)
a,bはベクトルです.
-2ωsin(ωt)da/dt + 2ωcos(ωt)db/dt + cos(ωt)d^2a/dt^2 + sin(ωt)d^2b/dt^2
の計算なんですが,0になれますか?
証明問題をやっていて,おそらくこの多項式は0になると踏んだのですが,計算が詰まってしまいました.ヒントをいただければお願いします.
Re: 計算問題
mNeji さんのレス (2009/05/12(Tue) 03:06)
冗談半分の話ですが,もし与式の係数2が1であって,次の式だとすると,
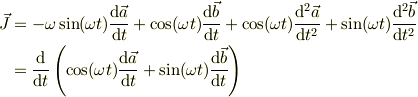
になるので,最後の大括弧の中が定ヴェクタなら, 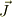 はゼロ・ヴェクタになります.
はゼロ・ヴェクタになります.
Re: 計算問題
mNeji さんのレス (2009/05/13(Wed) 13:19)
>微分の中が,定数なら良いんですね.
一つの可能性です.
>てことは,元の式では,0にはなれなかったってことですか?
ちなみに,残りを変形してみると,
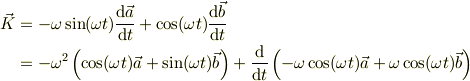
とも変形出来ますね.
Re: 計算問題
toorisugari no Hiro さんのレス (2009/05/13(Wed) 13:43)
> 証明問題をやっていて,おそらくこの多項式は0になると踏んだのですが,
元の証明問題を出してくれた方が解決が早そうです.
Re: 計算問題
数学迷い人 さんのレス (2009/05/13(Wed) 14:06)
元の問題です.↓
ベクトルX=(cosωt)a +(sinωt)bに対して,
d^2X/dt + ω^2X = 0
X×X’=ωa×bを示すという問題です.
Re: 計算問題
数学迷い人 さんのレス (2009/05/13(Wed) 14:11)
ちなみに,ベクトルを微分しても,ベクトルなのでしょうか? 変な質問ですが,お願いします.
Re: 計算問題
toorisugari no Hiro さんのレス (2009/05/13(Wed) 19:46)
「ベクトル 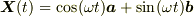 に対して,
に対して,
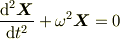
および,
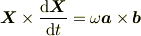
を示せ.」という問題ですか.
 は定数,
は定数, 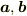 は定ベクトルですね.そうでないと解けません.
は定ベクトルですね.そうでないと解けません.
Re: 計算問題
toorisugari no Hiro さんのレス (2009/05/13(Wed) 19:53)
> ちなみに,ベクトルを微分しても,ベクトルなのでしょうか?
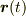 のようなベクトル値関数を微分した
のようなベクトル値関数を微分した 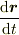 もベクトルです.
もベクトルです.
なぜなら,定義により,
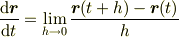
ですが,極限を取る前の 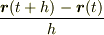 はベクトルの差
はベクトルの差 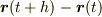 をスカラ
をスカラ 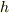 で割ったものですからベクトルになります.当然,その極限もベクトルです.
で割ったものですからベクトルになります.当然,その極限もベクトルです.
# ベクトルにベクトルを足しても(引いても)ベクトル
# ベクトルにスカラをかけても(割っても)ベクトル
# ベクトル値関数 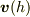 の極限
の極限 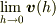 の値もベクトル
の値もベクトル
Re: 計算問題
mNeji さんのレス (2009/05/14(Thu) 10:17)
>定ベクトルを微分したら,0ということですよね? >ということなら問題解けました.
私には,「数学迷い人さんの考え方」も興味深いのですが,それ以上に,「解こうとされている問題」が不思議に見えます.
もし宜しかったら,ご質問の問題は,どのような所にあったのか教えてくださると助かります.
Re: 計算問題
数学迷い人 さんのレス (2009/05/14(Thu) 10:54)
>もし宜しかったら,ご質問の問題は,どのような所にあったのか教えてくださると助かります.
この問題は,ベクトル解析の授業での問題です.今,ベクトルの微分という章に入りました. 疑問に思ったことは,ベクトルでの微分扱いです. 直線であるベクトルを微分するということがイメージしにくかったです. また,定ベクトルを微分したら,0になることがわからなかったです. 定ベクトルというのは,ベクトルXでの要素のひとつであると考えています.
Re: 計算問題
mNeji さんのレス (2009/05/14(Thu) 12:32)
>この問題は,ベクトル解析の授業での問題です.今,ベクトルの微分という章に入りました.
なるほど,判りました.ご説明,有り難うございました.
>疑問に思ったことは,ベクトルでの微分扱いです.
このように,直接的に質問される方が,回答は付き易いです.
>直線であるベクトルを微分するということがイメージしにくかったです. >また,定ベクトルを微分したら,0になることがわからなかったです. >定ベクトルというのは,ベクトルXでの要素のひとつであると考えています.
ここら辺は,確実に理解出来てないと,先に行けば行く程判らなくなると思うので,納得できるまで頑張って下さい.
すでに,toorisugari no Hiroさんが,No.23767で解説されていますが,それと合わせて,質問されると良いのではないでしょうか?
ヒョットして,「ベクトル間の足し算,引き算」のときに,平行移動するのに抵抗が在るとか?私自身も,この疑問にトラップされたような気がします.
Re: 計算問題
mNeji さんのレス (2009/05/14(Thu) 14:55)
位置ベクトル 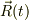 と速度ベクトル
と速度ベクトル 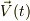 とすると,
とすると,
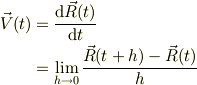
と書かれます.
これを図で考えます.ただし,「 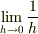 」を面倒なので省略して,単に「
」を面倒なので省略して,単に「 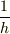 」としますが,極限記号は付いているとして読んでください.簡単の為に,一次元のベクトルの表記を考えます.
」としますが,極限記号は付いているとして読んでください.簡単の為に,一次元のベクトルの表記を考えます.
原点Oから,右の方向を正とします.ベクトルの始点を「・」,ベクトルの終点を「←」や「→」とし,ベクトルの長さを「ー」で表すとします.
・原点から3単位右の位置ベクトルを
「 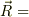 (・ーー→)」
(・ーー→)」
・原点の位置ベクトル,言い換えれば,ゼロ・ベクトルを
「 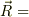 (・)≡(ゼロ)=0」
(・)≡(ゼロ)=0」
#ゼロ・ベクトルは本来,「 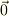 」と書いた方が良いかも知れませんが,スカラのゼロ,「
」と書いた方が良いかも知れませんが,スカラのゼロ,「  」で代用していますね.
」で代用していますね.
・原点から2単位左の位置ベクトルを
「 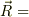 -(・ーー→) ≡ (←ーー)」
-(・ーー→) ≡ (←ーー)」
・従って, 「(ゼロ) = (←ーー) +(・ーー→) = -(・ーー→) +(・ーー→) = (←ーー) -(←ーー) 」
〜〜〜〜 以上の準備のもとで,
具体的に,位置ベクトルが時間と共に増えている場合を図示します;
「 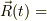 (・ーー→)」
「
(・ーー→)」
「 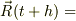 (・ーーーーー→)」
(・ーーーーー→)」
「 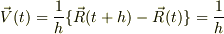 {(・ーーーーー→)-(・ーー→)}
{(・ーーーーー→)-(・ーー→)} 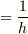 (・ーーー→)」
(・ーーー→)」
位置ベクトルが時間に依らず一定の定ベクトルの場合には;
「 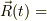 (・ーー→)」
「
(・ーー→)」
「 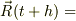 (・ーー→)」
(・ーー→)」
「 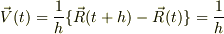 {(・ーー→)-(・ーー→)}
{(・ーー→)-(・ーー→)} 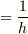 (・)
(・)  」
」
Re: 計算問題
toorisugari no Hiro さんのレス (2009/05/14(Thu) 16:22)
> 定ベクトルを微分したら,0になることがわからなかったです.定ベクトルというのは,ベクトルXでの要素のひとつであると考えています.
ここではベクトルとはベクトル値関数のことです.つまり,
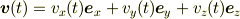
のような形を「ベクトル」と呼んでいます.一般には  が変化すると,
が変化すると, 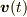 も変化します.
も変化します.
定ベクトルとは  によらず一定値をとるベクトル値関数です.先の記事で示した微分の定義により,定ベクトルを
によらず一定値をとるベクトル値関数です.先の記事で示した微分の定義により,定ベクトルを  で微分したら
で微分したら  です.
です.
デカルト座標系の基底 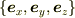 も定ベクトルです(極座標などの他の座標系ではそうなるとは限りません).
も定ベクトルです(極座標などの他の座標系ではそうなるとは限りません).
# ま,考えてみればなじみの表現
も不思議ですよね. 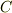 は数であって関数でないのに何故微分していいのだろう.
は数であって関数でないのに何故微分していいのだろう.