divuとrotuの物理的意味

divuとrotuの物理的意味

dai さんの書込 (2009/05/10(Sun) 18:27)

連続体の変形を考える上で，uを変位ベクトルとしたとき， divuは体積変化率を意味するそうですが （筑波大学物理学系谷口伸彦先生物理学B3講義ノート（２００４年度）P40(PDF)を参考にさせていただいています）， divuは歪みテンソルと同意と思っていました． 体積変化率と歪みテンソルの違いはどこにあるのですか？

また，rotuにはどのような意味があるのですか？ これも歪みテンソルとは違うのですか？

物理的な意味が捕らえきれないため，先に進めず困っています．

どなたか助言をいただけないでしょうか．よろしくお願いします．

Re: divuとrotuの物理的意味

toorisugari no Hiro さんのレス (2009/05/11(Mon) 09:26)

変位ベクトルを 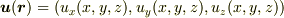\bm{u}(\bm{r})=(u_x(x,y,z),u_y(x,y,z),u_z(x,y,z)) としたとき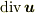， \mathrm{div\,}\bm{u} は

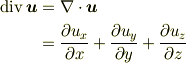
\mathrm{div\,}\bm{u} &=\nabla\cdot\bm{u}\\&= \frac{\partial u_x}{\partial x} + \frac{\partial u_y}{\partial y} + \frac{\partial u_z}{\partial z}

となるスカラです．その値は，微小な直方体の各頂点が 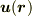\bm{u}(\bm{r}) で変位したときの体積の増分比を表します．

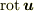\mathrm{rot\,}\bm{u} は

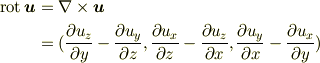
\mathrm{rot\,}\bm{u} &=\nabla\times\bm{u}\\&= (\frac{\partial u_z}{\partial y} - \frac{\partial u_y}{\partial z}, \frac{\partial u_x}{\partial z} - \frac{\partial u_z}{\partial x}, \frac{\partial u_y}{\partial x} - \frac{\partial u_x}{\partial y})

となるベクトルです．その値は，微小な直方体の各頂点が 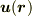\bm{u}(\bm{r}) で変位したときの，平均化された回転角度(の2倍)を表します．(ベクトルの方向は回転軸に平行です．)

テンソルとスカラとベクトルはそもそも違う量です． まずはベクトル解析から勉強してください．

Re: divuとrotuの物理的意味

リモコン さんのレス (2009/05/11(Mon) 19:53)

発散と回転の物理的な意味は「物理のかぎしっぽ」を始まりとしたさまざまなサイトで紹介されています．

等々・・・・・ いろいろとインターネットで検索すると情報が得られますよ．

私もベクトル解析に関する知識はインターネットから得ました

Re: divuとrotuの物理的意味

dai さんのレス (2009/05/11(Mon) 20:58)

toorisugari no Hiroさん，リモコンさん，ありがとうございます．

今もベクトル解析について見直しているところです． 一冊の教科書だけでは理解できなかった所が，インターネットの情報で同じような内容をいろいろなサイトで確認して，物理的意味がつながってきました．

ありがとうございました．