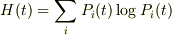マスター方程式におけるボルツマンのH定理

home > 掲示板 >

このページのPDF版

サイトマップ

マスター方程式におけるボルツマンのH定理

えりさんの書込 (2009/05/06(Wed) 16:00)

$H(t)=\sum_{i}P_{i}(t)\log{P_{i}(t)}$

という関数を考えると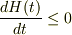， $\frac{dH(t)}{dt}\leq0$ となることを示せ．

という問題で，解いてみたのですが，以下のアプローチに自信がありません．

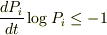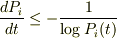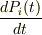まず，H(t)をtで微分して， $\frac{dH(t)}{dt}=\sum_{i}[\frac{dP_{i}(t)}{dt}\log{P_{i}(t)}+P_{i}(t)\frac{d}{dt}\log{P_{i}(t)}]$ $=\sum_{i}[\frac{dP_{i}(t)}{dt}\log{P_{i}(t)}+1]$ これがこれが負であることを示す． $\frac{dP_{i}}{dt}\log{P_{i}}\leq-1$ …（＊）を示す． $\frac{dP_{i}}{dt}\leq-\frac{1}{\log{P_{i}(t)}}$ …これをグラフを利用して解こうと思ったのですが，（＊）とした時点で，シグマを無視してしまっているので，ダメなような気がしているのですがどうなのでしょうか？まず，マスター方程式を使っていないので，それも間違っているような気がします．やはり， $\frac{dP_{i}(t)}{dt}$ にマスター方程式を使わなくてはいけないのでしょうか？

どなたか助言をいただけないでしょうか．よろしくお願いします．

Re: マスター方程式におけるボルツマンのH定理

mNeji さんのレス (2009/05/06(Wed) 11:26)

難しい領域に踏み込まれている様ですね．ちょっとYahooで「マスター方程式ボルツマン H定理」を検索してみると，そのトップに，

＞非平衡・非線形の物理(PDF) ＞ http://soliton1.ph.sci.toho-u.ac.jp/nonlinb.pdf

という資料の第3章に，類似した論議が在るようです．ご参考まで．

Re: マスター方程式におけるボルツマンのH定理

えりさんのレス (2009/05/07(Thu) 15:15)

返信ありがとうございます．一筋縄ではいかないようですね…びっくりしました．

一回じっくり読んで考えてみようと思います．どうもありがとうございました．

Re: マスター方程式におけるボルツマンのH定理

えりさんのレス (2009/05/10(Sun) 16:38)

時間が空いてしまいました． mNeji様が教えて下さったページの15ページ最下行についてなのですが，dH/dtは本当にそうなるのでしょうか？

私は $=\sum_{i}[\frac{dP_{i}(t)}{dt}\log{P_{i}(t)}+1]$ のようにはできると思いますが， dP/dtで全体をくくることはできないと思うのです．

どうなのでしょうか？ご意見お聞かせ下さい．

Re: マスター方程式におけるボルツマンのH定理

mNeji さんのレス (2009/05/10(Sun) 16:50)

これから外出するので，ちょっと気になる点を；＞まず，H(t)をtで微分して，＞ $\frac{dH(t)}{dt}=\sum_{i}[\frac{dP_{i}(t)}{dt}\log{P_{i}(t)}+P_{i}(t)\frac{d}{dt}\log{P_{i}(t)}]$ ＞ $=\sum_{i}[\frac{dP_{i}(t)}{dt}\log{P_{i}(t)}+1]$

最後の式は， $=\sum_{i}\left(\frac{dP_{i}(t)}{dt}[\log{P_{i}(t)}+1]\right)$ のような気がしますが...．

Re: マスター方程式におけるボルツマンのH定理

えりさんのレス (2009/05/10(Sun) 19:33)

すみませんでした．．そうですね，後ろの 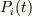$P_{i}(t)$ も微分しなくてはいけないですよね（汗これでまたやってみます．

Re: マスター方程式におけるボルツマンのH定理

えりさんのレス (2009/05/10(Sun) 20:18)

このdH/dtの式変形は，ただの算数的な変形ではないのでしょうか？ 16ページの1行〜2行の変形が，何をしているのか読み取れないのですが，物理的な関係を用いているのでしょうか…？

Re: マスター方程式におけるボルツマンのH定理

mNeji さんのレス (2009/05/10(Sun) 21:07)

やはり，講義で出て来たマスター方程式[pdfで言えば式(3.1)に相当する筈でしょうが]を，適用する必要が有るのではないでしょうか．

ただ，いま論じられているのは，まだ定常状態に至っていない場面なので，マスター方程式がどのようになるのかはpdfとは違いでしょう．

ただ，最後の式は，

$&=\sum_{i}\left(\frac{dP_{i}(t)}{dt}[\log{P_{i}(t)}+1]\right)\\&=\sum_{i}\frac{dP_{i}(t)}{dt}\log{P_{i}(t)} +\sum_{i}\frac{dP_{i}(t)}{dt}\\&=\sum_{i}\frac{dP_{i}(t)}{dt}\log{P_{i}(t)} +\frac{d}{dt}\sum_{i}P_{i}(t)\\&=\sum_{i}\frac{dP_{i}(t)}{dt}\log{P_{i}(t)}$

となり，少しは簡単か？

＞16ページの1行〜2行の変形が，何をしているのか読み取れないのですが，＞物理的な関係を用いているのでしょうか…？

これって，式(3.4)の直ぐ下の説明；

＞途中 m と n の入れ替えを何度か使い,また遷移確率に関する詳細釣り合いの関係式も用いている．さらに任意の負でない実数 x,y に対して一般的に成り立つ不等式 ...以下略

では駄目ですか？

Re: マスター方程式におけるボルツマンのH定理

なんとなくさんのレス (2009/05/10(Sun) 22:41)

横レス失礼，なんとなくです．蛇足かも知れませんが，一応．最初の質問はお気づきのように，d/dt(log(f(x))=df(x)/dx・(1/f(x))の適用ミス，ｐ１６の１〜２行目はただ，Σ添字m,nの対称性を利用して入れ替えただけです（符号に注意）．

Re: マスター方程式におけるボルツマンのH定理

えりさんのレス (2009/05/10(Sun) 22:42)

1行〜2行目でも既に

＞途中 m と n の入れ替えを何度か使い,また遷移確率に関する詳細釣り合いの関係式も用いている．さらに任意の負でない実数 x,y に対して一般的に成り立つ不等式 ...以下略

を使っているんですか！？私には1行目と2行目が全く違う式に見えるのですが…

Re: マスター方程式におけるボルツマンのH定理

えりさんのレス (2009/05/10(Sun) 22:45)

なんとなく様，時間ですれ違ってしまいました，ごめんなさい．

＞ｐ１６の１〜２行目はただ，Σ添字m,nの対称性を利用して入れ替えただけです（符号に注意）．

これは2行目から3行目のことではないのでしょうか？

Re: マスター方程式におけるボルツマンのH定理

なんとなくさんのレス (2009/05/10(Sun) 23:08)

そうです．１〜２行目もです．単純ですから書いておきます．（定数項は省き簡略化しています） Σ(-WmnP(n)+WnmP(m))(lnP(n)+1) =Σ{-WmnP(n)lnP(n)+WnmP(m)lnP(n)-WmnP(n)+WnmP(m)} （第３，４項は同じものによりキャンセル） =Σ{-WmnP(n)lnP(n)+WnmP(m)lnP(n)} =-Σ{WmnP(n)lnP(n)-WnmP(m)lnP(n)} （第２項の添字nとmを入れ替える） =-Σ{WmnP(n)(lnP(n)-lnP(m))} となります．

Re: マスター方程式におけるボルツマンのH定理

えりさんのレス (2009/05/10(Sun) 23:45)

3,4項は同じものなんですか！？もしかして， -WmnP(n)+WnmP(m)=-WmnP(n)+WmnP(n) ということですか？

Re: マスター方程式におけるボルツマンのH定理

なんとなくさんのレス (2009/05/11(Mon) 00:08)

>えりさん >-WmnP(n)+WnmP(m)=-WmnP(n)+WmnP(n)

と言うより，あくまでΣを取るときのn,m対称性で入れ替えただけです．n,mをただのサフィックスと考えて良いということです．つまり項毎に成り立たなくても全体和として同じものになります．上式右辺は当たり前ですが，左辺は単独で言えるかどうかは分かりません．つまり，意味は添字n,mという記号にあるのではなくて，順番が重要です．くどいようですが，日本語にしてみます．左辺第一項：状態mからnへの遷移確率×状態nの実現確率左辺第二項：状態nからmへの遷移確率×状態mの実現確率これをn,mに関してΣするということなので，入れ替えても同じ事を表していることが分かります．ΣAiBj=ΣAjBi(for all i,j)ということです．

Re: マスター方程式におけるボルツマンのH定理

えりさんのレス (2009/05/11(Mon) 00:21)

なるほど．項毎に見るのではなくて，あくまでも全体和を考えてn,mを入れ替えているのですね．

そうしていくと，4行目のシグマの直後の[]の中はキャンセルして消えてしまいそうなのですが，それは違うのでしょうか？（時間も遅いので返信はすぐでなくても大丈夫です）

Re: マスター方程式におけるボルツマンのH定理

なんとなくさんのレス (2009/05/11(Mon) 00:37)

>えりさんこれが最後となるかも知れませんが．４行目はΣ(AiBj-AjBi)×(Cj-Di)の形をしています．Σ直後だけの[]を足し上げてはいけません．かけ算なのであくまで乗算が先です．先ほども書いたように[]の中味がキャンセルしているのではないからです．ついでに言えば，４行目は逆にキャンセルする項をわざと足して，対称性をもたせた形に変形しているわけです（ΣAiBj=1/2Σ(AiBj+AjBi)のように，1/2が付く）．勿論展開すれば３行目に戻ります．イヤミではないのですが，答えを先走って良くなかったかも知れません．じっくり考えてみてください．検討を祈ります．

Re: マスター方程式におけるボルツマンのH定理

えりさんのレス (2009/05/11(Mon) 00:46)

大変丁寧に解説してくださり，頭が下がる思いです…．本当にどうもありがとうございます．

確かに答えを先走って空回りをしてしまっていたようです．もう一度頭を冷やして計算してみようと思います．

遅くまでお付き合いいただき，本当にありがとうございました．

[home] [掲示板] [ページの先頭]