斜面の運動
斜面の運動
ヒノッキー さんの書込 (2009/05/03(Sun) 19:28)
こんばんは.高校物理の問題で,腑に落ちない部分があったので, 力を貸してもらいに来ました.
滑らかな床の上に,質量Mの三角台をおく斜面の角度θとし,
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/03(Sun) 19:42)
あ・・・.すみませんパソコンの操作を誤りました. もう一度書きます.
滑らかな床の上に,質量Mの三角台をおく. 斜面の角度をθとし, その斜面上に質量mの小物体を置いて静かに離す. このとき,小物体の鉛直方向の速度の大きさをu,水平方向の速度の大きさをv, 三角台の速度の大きさをVとすると,u,v,Vの間に成り立つ関係を表す式を書け.
この問題の解答は,u/(v+V)=tanθとなっていたのですが, なぜこの形になるのか,いまいち理解できません. 運動方程式を用いて計算すると, u/(v+V)==m/(m+M)×tanθ となってしまうのです.
説明の不備などがありましたら,書き加えますので, 解答となる理由を教えていただけませんか?
P.S.Yokkunさん,前回の統計力学の問題はありがとうございました. お礼をしていなかったので,ここでさせてもらいます.
Re: 斜面の運動
Yokkun さんのレス (2009/05/03(Sun) 23:21)
ヒノッキーさん,こんばんは.
>運動方程式を用いて計算すると, u/(v+V)==m/(m+M)×tanθ
これは,運動方程式の問題ではないのです. 相対速度の問題で,斜面から見た速度の方向は斜面下向きということを数学的に表そうということで,運動方程式の問題の前段ですね.
Re: 斜面の運動
mNeji さんのレス (2009/05/04(Mon) 00:40)
別意見を述べてみます.
運動方程式を立てる場合,慣性系から組み立てるのが解り易いと思います.それから,三角台から見た方程式を出すと良いでしょう.
三角台の置いてある平面の水平方向を 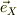 ,垂直方向を
,垂直方向を 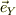 の方向ヴェクタとします.この座標から,三角台の一点Tの座標,
の方向ヴェクタとします.この座標から,三角台の一点Tの座標, 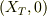 とします.この点から,斜面方向に
とします.この点から,斜面方向に 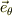 ,斜面に垂直方向を
,斜面に垂直方向を 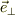 とします.
とします.
三角台の位置ヴェクタ;
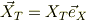
小物体の位置ヴェクタ;
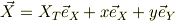
小物体と三角台には垂直抗力しか無いので,三角台から小物体に作用する 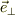 方向の抗力の大きさをFとすると,
方向の抗力の大きさをFとすると,
小物体の運動方程式は,
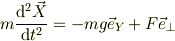
で,三角台は小物体によって変形しない,言い換えると, 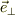 方向に加速度を生じない束縛条件からFが決まります.
方向に加速度を生じない束縛条件からFが決まります.
三角台の運動方程式は, 水平面からの垂直抗力Gとして
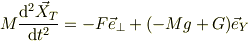
となり,水平面は三角台によって変形しない,言い換えると 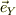 方向に加速度を生じない束縛条件からGが決まります.
方向に加速度を生じない束縛条件からGが決まります.
ここで,方向ヴェクタ間に
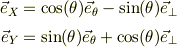
また速度の表現から,
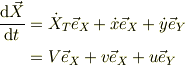
として,Vの符号と,(vやu)の符号は逆である事に注意して下さい.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/04(Mon) 01:27)
Yokkunさん,mNejiさん,ありがとうございます. ようやく,問題の意味を理解することができました.
相対運動で考えれば,いいだけの問題なのですね. これに引っ掛かってたことが恥ずかしいです・・・.
Re: 斜面の運動
mNeji さんのレス (2009/05/04(Mon) 02:23)
小物体の運動方程式は,
![m\frac{\mathrm{d}^2\vec X}{\mathrm{d} t^2}&= -mg\vec e_Y +F\vec e_{\perp}\\&= -mg[\sin(\theta)\vec e_{\theta}+\cos(\theta)\vec e_{\perp}] +F\vec e_{\perp}\\&= -mg\sin(\theta)\vec e_{\theta} +[F -mg\cos(\theta)]\vec e_{\perp}](http://hooktail.maxwell.jp/bbslog/c23b799783b6afe4cb676389fb909447.png)
となりますから,束縛条件から,抗力は ![[F -mg\cos(\theta)]=0](http://hooktail.maxwell.jp/bbslog/ee11eb4c69b1966442bc8089d89619ec.png) を満たすことになる;
を満たすことになる;
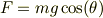
同様に,三角台の運動方程式から
![M\frac{\mathrm{d}^2\vec X_T}{\mathrm{d} t^2}&= -F\vec e_{\perp} +(-Mg +G)\vec e_Y\\&= -F[-\sin(\theta)\vec e_X + \cos(\theta) \vec e_Y]+(-Mg +G)\vec e_Y\\&= F\sin(\theta)\vec e_X +[-F\cos(\theta) -Mg +G]\vec e_Y](http://hooktail.maxwell.jp/bbslog/b3375bf3dc9f05ef888bfe55a7821fbd.png)
となり,束縛条件から,
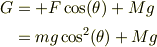
となるようですね.
#このような面倒な問題を見つけられるものですね. #では,実際の速度,V,v,uを出してみて下さい(笑).
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/04(Mon) 02:36)
えー・・・と(笑) u = g×cosθ×cosθ×t v = M/(M+m)×g×sinθcosθ×t V = m/(M+m)×g×sinθcosθ×t
だと思います.問題文では,速度の大きさをu,v,Vとしているので, マイナスは省きました.(今度は,TeXの勉強をしてから来ます・・・)
加速系で考えると, Fの値は,mgcosθで, Gの値は,Fcosθ+Mg となり,簡単に記述できるが,これは加速する系なので, もし慣性系で考えるときは,F,Gの値が,三角台の加速度に依存する・・・ と,いうことでいいのでしょうか?
Re: 斜面の運動
Yokkun さんのレス (2009/05/04(Mon) 08:35)
斜面もなめらかなのですよね?
慣性系(床に対して静止した座標系)から見ても加速系(三角台に対して静止した座標系)から見ても成立する式は同じです.ただ,加速系では自身の加速度を含む項を慣性力と見るわけですね.この問題は,初めから加速系で運動方程式を立てるのがすっきりする特別な例です.小物体の斜面への束縛条件が,慣性系からは相対運動を考えることになりやっかいなのですね.
小物体の運動方程式
斜面方向 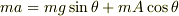 垂直方向
垂直方向 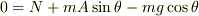 または,
水平方向
または,
水平方向 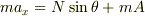 鉛直方向
鉛直方向 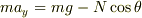 紛らわしいですが,加速度はすべて運動方向を正としました.
紛らわしいですが,加速度はすべて運動方向を正としました.
水平方向の運動方程式は,慣性系から見ると
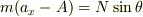 となり,
となり,
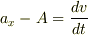 が正真の加速度です.
が正真の加速度です.
もちろん,台の運動方程式は慣性系で立てなければなりません.
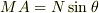
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/04(Mon) 10:24)
なるほど,慣性力のmAをすっかり忘れていたので, 変になって,どツボにはまっていたことがはっきりしました.
どうもありがとうございました!
Re: 斜面の運動
mNeji さんのレス (2009/05/04(Mon) 10:48)
私は,「慣性力」というのは両刃の剣だと思うので,極力利用しない様にしています.そこで運動方程式に従って,速度を出すことを示します.
三角台の運動方程式の 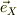 成分から,
成分から,
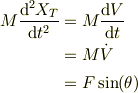
より,
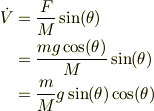
小物体の運動では,
![\frac{\mathrm{d}\vec X}{\mathrm{d} t}&= (V + v)\vec e_X + u\vec e_Y\\&= (V+v)\cos(\theta)\vec e_{\theta}-\sin(\theta)\vec e_{\perp} +u\sin(\theta)\vec e_{\theta}+\cos(\theta)\vec e_{\perp}\\&= [(V+v)\cos(\theta) +u\sin(\theta)]\vec e_{\theta} +[-(V+v)\sin(\theta) +u\cos(\theta)]\vec e_{\perp}](http://hooktail.maxwell.jp/bbslog/e6cd7384f563b49e1f536604fef0ec58.png)
だから,拘束条件から 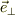 成分はゼロとなるので,
成分はゼロとなるので,
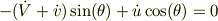
非拘束面( 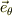 )の方向成分の運動方程式として,
)の方向成分の運動方程式として,
![m[(\dot V+ \dot v)\cos(\theta) +\dot u\sin(\theta)] = -mg\sin(\theta)](http://hooktail.maxwell.jp/bbslog/182744dfdd4bcf7616543af5eac61a64.png)
この2式から,v,uを求める事ができる.そこで,
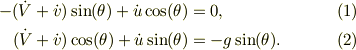
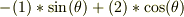 から
から
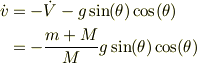
同様に,
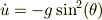
【追伸】
基に戻って,出題の関係式を眺めた所,式(1)と等価な式な様にも思えますが,どうなんでしょうか.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/04(Mon) 12:12)
初期条件がすべて静止状態で,u,v,Vの一階微分には, tに依存する項が含まれていないので, 積分したのち,tを消去すれば確かに同じ式になります. ですので,(1)と出題の関係式は確かに等価です.
vとVの値について質問です. 運動方程式を解いたところ,確かにこの値になりました. しかし,これでは水平方向の運動量保存を満たしていない気がするのです.
mv+MV=0 これが運動量保存の式になると思いますが, 方程式から求めたv,Vの値では,この式を満たしません. これは,いったいどういうことでしょうか?
Re: 斜面の運動
Yokkun さんのレス (2009/05/04(Mon) 12:28)
私の立てた運動方程式で説明すると,
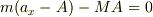 これを積分するとただちに,
これを積分するとただちに,
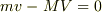 を得ます.
を得ます.
垂直抗力は, 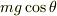 にはなりませんよ.その部分で間違えたのではないでしょうか?斜面に垂直な成分もつりあってはいないのです.つりあいを考えるためには,加速系に乗るわけですから慣性力を落とせないのですね.
今日は午前中からちょっと野暮用があったものですから,mNejiさんの議論は精査していませんが,
にはなりませんよ.その部分で間違えたのではないでしょうか?斜面に垂直な成分もつりあってはいないのです.つりあいを考えるためには,加速系に乗るわけですから慣性力を落とせないのですね.
今日は午前中からちょっと野暮用があったものですから,mNejiさんの議論は精査していませんが, 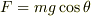 と置いてしまったのが失敗の始まりのように思います.束縛条件は台も加速度運動していますから,そのようにはいかないのです.小物体の下降する方向は傾き角
と置いてしまったのが失敗の始まりのように思います.束縛条件は台も加速度運動していますから,そのようにはいかないのです.小物体の下降する方向は傾き角  にはなりません.
にはなりません.
私の式では,斜面に垂直な方向の式を書き換えると,
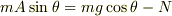 となります.垂直抗力は
となります.垂直抗力は 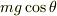 より小さくなり,そのために加速度
より小さくなり,そのために加速度 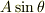 をもつことになるわけです.これが束縛条件にとって変わります.
をもつことになるわけです.これが束縛条件にとって変わります.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/04(Mon) 13:03)
なるほど.Fを求める際,三角台の動きをすっかり忘れてました. 慣性力は見落としてしまいがちです・・・. だから問題は運動方程式を出さずに,v,u,Vの関係式を求めさせたのですね.
運動方程式だけではこの問題は解くことは難しいことがよくわかりました. どうもありがとうございます!
Re: 斜面の運動
Yokkun さんのレス (2009/05/04(Mon) 13:12)
もちろん,慣性力を持ち出さずmNejiさんのように徹底して慣性系に立った運動方程式を書いてもいいのです.ただ,同じ式の解釈が変わるだけですね.ただし,斜面自体の運動を考慮しなければならなくなるので,束縛条件が一筋縄ではいかないことに注意しなければなりません.その点むしろ加速系に立ちきってしまう方が考察がちょっとラクになる場合もあるのですね.運動方程式が,慣性力を含むつりあいに変わるだけで結果は同じですから,要はどちらが考えやすいかということです.こうした立場の乗換えが上手になると,両方の立場からの解釈が自在になり,自信がもてるようになります.
Re: 斜面の運動
mNeji さんのレス (2009/05/04(Mon) 15:54)
>しかし,これでは水平方向の運動量保存を満たしていない気がするのです.
う〜む.「運動量保存」というような法則が成り立つには,「慣性系」から見ないと駄目ですね.恐らく,今論じている座標系を図示されていないのだと思います.また座標の方向をその場,その場で替えられている様ですが,余程注意深く操作しないといけません.
勿論,系全体の水平方向の運動量保存が成り立つとは思いますが,丁寧に考える事をお勧めします.
【追伸】
今の場合,求めるべきは,水平方向の運動量の総和です;
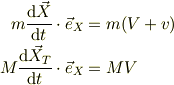
従って,保存するべき運動量は, 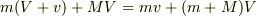 ,だろうと思います.
,だろうと思います.
【再追伸】
>運動方程式だけではこの問題は解くことは難しいことがよくわかりました.
この意味が理解出来ません.私は,慣性系から見た
- 小物体と三角台との運動方程式を作り,
- 小物体と三角台との相互作用力Fを導入し,斜面に垂直方向の束縛条件からFを決め,
- 三角台と水平面との相互作用力Gを導入し,水平面に垂直方向の束縛条件からGを決め,
- 三角台と小物体の運動方程式をときました.
これは,通常の力学で一般的な処方箋だと思っています.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/04(Mon) 16:34)
>(2) 小物体と三角台との相互作用力Fを導入し,斜面に垂直方向の束縛条件からFを決め,
この時点で,F=mgcosθとしてしまったことに間違いがあったのです. 垂直抗力と,重力の斜面に垂直な成分が等しくなるのは,三角台が動かない 時だけです.
Yokkunさんが言っていたように,F=mgcosθーmAsinθ となる必要があるのですが,Aは未知の項なので, 解くのが難しくなると表現しました.
Re: 斜面の運動
mNeji さんのレス (2009/05/04(Mon) 16:48)
>Yokkunさんが言っていたように,F=mgcosθ+Asinθ >となる必要があるのですが,Aは時間に依存する項なので, >解くのが難しくなると表現しました.
どのような根拠に基づいて,どんな結論が出て来ているのかちっとも判りません.むしろ,一度,完全に解いてから「Aは時間に依存する項」も含めてお示しにならないと,いけないと思います.
逆に,私の計算結果が問題の解答と食い違っている所があればお教え下さい.出来れば,出題が書かれている図書と,そのページをお教えくださると有難いです.
Re: 斜面の運動
Yokkun さんのレス (2009/05/04(Mon) 16:52)
mNejiさん,運動方程式を立てる際に斜面に垂直な成分に対してつりあっていることを前提してしまったことが間違いのもとです.斜面に垂直な方向にも小物体は加速度をもつのですから,その方向についても運動方程式を立てなければならなかったはずです.私は,三角台の加速度の大きさを 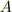 とおき,束縛条件を用いて小物体の斜面に垂直な加速度成分を
とおき,束縛条件を用いて小物体の斜面に垂直な加速度成分を 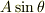 と評価したわけです.これは,加速系から見た立場では小物体が斜面垂直方向について
と評価したわけです.これは,加速系から見た立場では小物体が斜面垂直方向について 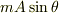 なる慣性力の成分を受けると解釈することもできます.
なる慣性力の成分を受けると解釈することもできます.
Re: 斜面の運動
mNeji さんのレス (2009/05/04(Mon) 17:02)
>斜面に垂直な方向にも小物体は加速度をもつのですから,その方向についても運動方程式を立てなければならなかったはずです.
それでは,具体的にどのように処理するのでしょうか?
# 私は,束縛条件こそが,その任を背負っていると理解しています. # 今回の私の計算では,小物体の座標を,三角台の座標と,そこから見た小物体の相対座標とに分けているので,小物体が三角台と平行に動いている事は保証されています.
部分的な式はちらほら書かれていますが,一度,完全な立式と,その解とでご説明くださいませんか?
Re: 斜面の運動
Yokkun さんのレス (2009/05/04(Mon) 17:29)
高校物理の問題とされていますので,ベクトルは成分表示に徹したいと考えます.また,mNejiさんの方針に沿って慣性系(静止系)に対する運動方程式を立てます.したがって,前に書いた小物体の加速度は加速系のものでしたが,慣性系から見たものにとりかえます.それを 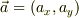 とおきます.ただし,便宜のため運動方向を正方向とします.
小物体の運動方程式は,
水平方向
とおきます.ただし,便宜のため運動方向を正方向とします.
小物体の運動方程式は,
水平方向 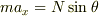 鉛直方向
鉛直方向 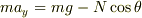 また,台の運動方程式は,
水平方向
また,台の運動方程式は,
水平方向 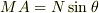 さて,この場合の束縛条件が問題です.これは,
さて,この場合の束縛条件が問題です.これは,
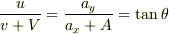 となります.
以上の4式から,
となります.
以上の4式から, 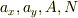 を得ます.もちろん,
を得ます.もちろん, 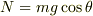 とはなりません.以上は水平・鉛直に成分を分けましたが,もちろん斜面方向と垂直方向に分けることも可能です.ただし,その場合もいずれも(つりあいではなく正真の)運動方程式になることに注意しなければなりません.
とはなりません.以上は水平・鉛直に成分を分けましたが,もちろん斜面方向と垂直方向に分けることも可能です.ただし,その場合もいずれも(つりあいではなく正真の)運動方程式になることに注意しなければなりません.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/04(Mon) 17:39)
すみません,この問題は某高校の試験の改変なので, 出題図書は分かりかねます.
小物体の斜面にたいする運動方程式は,
斜面に対して垂直方向: 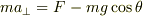 斜面方向:
斜面方向: 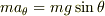 となると思います.
ここで,
となると思います.
ここで, 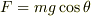 としてはいけません.
なぜなら,三角台が運動しているのに,垂直方向に動かなかったら,
三角台から離れてしまうからです.
としてはいけません.
なぜなら,三角台が運動しているのに,垂直方向に動かなかったら,
三角台から離れてしまうからです.
三角台の運動方程式: 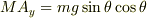 この水平方向の運動方程式を斜面に対する運動方程式に変形させると,
この水平方向の運動方程式を斜面に対する運動方程式に変形させると,
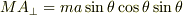
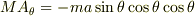 になると思います.
になると思います.
これより, 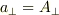 でなければ,斜面から離れてしまうので,
でなければ,斜面から離れてしまうので,
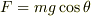 ではないことがわかります.
ではないことがわかります.
Re: 斜面の運動
mNeji さんのレス (2009/05/04(Mon) 17:58)
>ここで, 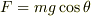 としてはいけません.
>なぜなら,三角台が運動しているのに,垂直方向に動かなかったら,
>三角台から離れてしまうからです.
としてはいけません.
>なぜなら,三角台が運動しているのに,垂直方向に動かなかったら,
>三角台から離れてしまうからです.
なにか高校の物理の問題は難しいですね.
そもそも,三角台が運動するのは,小物体が重力に引っ張られて落下し,その下に在る三角台と相互作用F(作用反作用の法則)で,三角台と垂直な方向に力を交換するからです.
そのように明確な相互作用のもとに小物体と三角台が動くので,ご質問の全体系の水平方向の運動量保存が成り立ちます.
でも,私は高校の物理の現状を知らないし,今回の問題も初めて見て驚いた位です.これ以上,自分の理解は進展できないので,この論議から撤退したいと思います.
Re: 斜面の運動
mNeji さんのレス (2009/05/04(Mon) 18:38)
Yokkunさん,
>もちろん, 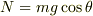 とはなりません.
とはなりません.
では,そのNは,連立方程式を解いた結果どうなるのですか?
私には,ご説明が不可知論になっているように思います.座標系の取り方を明確にしないのと,小物体と三角台との作用反作用を明確にしないのが問題だと思います.
また,水平方向の運動量保存の論議も理解出来ませんでした.私は,大昔の高校で教師の説明に理解が出来なかった落ちこぼれですので,このように複雑な問題を正しく理解出来ない可能性を排除できません.
でも,今回のYokkunさんのご説明には理解出来ない所が在りすぎます.が,現行の高校教育からみると,私の解釈が間違っている可能性が在りそうなので,今後の論議を差し控えたいと思います.
Re: 斜面の運動
Yokkun さんのレス (2009/05/04(Mon) 18:58)
mNejiさん,ご自分の誤りは十分認識できる範囲だと思われます.つまり慣性系から見たときに,小物体の運動は斜面に平行(傾き角θ)の方向ではないのです.台が後退しているのですから,運動方向は傾き角θより大きくなるはずです.
もうひとつ勘違いされているのは,問題では慣性系から見た小物体の水平速度成分がvとされているのに,mNejiさんは台に対する水平相対速度をvとされている点です.
計算結果を示します.
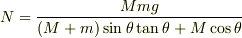
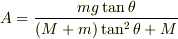
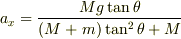
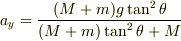
ただし,これはmNejiさんと成分分解方向が異なるので,ヒノッキーさんのものが(あっているかどうか精読してませんが)それに当たると思います.
>座標系の取り方を明確にしないのと,小物体と三角台との作用反作用を明確にしないのが問題だと思います.
これは,mNejiさんの流れに沿わなかった私の勇み足です.すみませんでした. 私の運動方程式では,小物体の座標は水平鉛直に分けて運動方向を正にとっています.一方台の方も台の運動方向を正にとっています.つまりいずれの加速度成分も正にとったのです.小物体と台との作用反作用は,水平成分に明らかです.なお台の鉛直成分は通常つりあいによって床からの抗力を得るだけなので省略しました.
Re: 斜面の運動
Yokkun さんのレス (2009/05/04(Mon) 19:23)
mNejiさんの流れに沿って議論を立て直します.
小物体の運動で
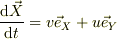 となるところが違います.慣性系から見た速度成分は
となるところが違います.慣性系から見た速度成分は  でよいのです.
でよいのです.
したがって,拘束条件も同様の理由によって間違っているのです.最初の問題をもう一度お読みいただければお気づきになるのではないでしょうか.mNejiさんの誤りは単にここだけです.
Re: 斜面の運動
mNeji さんのレス (2009/05/04(Mon) 20:44)
>となるところが違います.慣性系から見た速度成分は  でよいのです.
でよいのです.
仰るよう 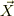 は,慣性系(水平面のどこかの一点からみた座標)から小物体の位置座標O-XYです.しかし,O-XYだど束縛条件の付与が複雑になるので,三角台の一点Tから見た非慣性系からの相対座標T-xyを導入しました.
は,慣性系(水平面のどこかの一点からみた座標)から小物体の位置座標O-XYです.しかし,O-XYだど束縛条件の付与が複雑になるので,三角台の一点Tから見た非慣性系からの相対座標T-xyを導入しました.
そもそも,小物体の座標は「問題で明確に記述されていないと感じた」ので,自分でNo.23652に於いて定義して使いました.その後の論議で,問題との整合性に破綻を起こしていない様なので,正しいだろうと推定していました.
ただ,今回の論議には,「合う・合わない」以前の考え方に不一致が在るので,これ以上の論議は不可能と思います.
特に,高校生さんで,受験勉強の一環で見られている方々に「間違いの無い考え方」を示す自信が無いので,これ以上の発言を控えたいと思います.
Re: 斜面の運動
Yokkun さんのレス (2009/05/04(Mon) 21:09)
>「合う・合わない」以前の考え方に不一致
があるとは私は認識していません.ただし,私がはじめた回答の流れで,ひとまず精査できなかったmNejiさんの議論をわきにおいて,ヒノッキーさんの認識にかかる表現をしただけのことです.mNejiさんの流れでの表記は,mNejiさんのおっしゃる高校物理教育への不満から,ていねいにベクトル微分方程式を分解していく処方であることは理解しております.そして,その点について私は共感もしています.しかし,現在の高校で物理の授業時間数を考えると私やmNejiさんの時代からしてもとんでもなく圧縮されて,ベクトルも微積分もご存知の通り物理においては中途半端なのです.そして,mNejiさんの表記を読める高校生はよほど優秀で特別な存在だと思います.したがって,失礼を承知で私がはじめた流れをおしとおしてしまいました.私はmNejiさんの方法論はていねいですばらしいと思っていますし,それに沿った議論をする準備はいつも整えているつもりです.この点だけはご理解いただきたいと思っております.
>小物体の座標は「問題で明確に記述されていないと感じた」ので
少なくとも推奨される座標軸の方向は明確にされています(もちろん座標軸はどのように立ててもまったく自由です).v,u,Vの定義によっています.もし,v,u,Vをはじめの問題にそって使われるのならば紛れはないと思います.ところが,mNejiさんはvを台に対する相対速度成分として使われているところが違います.No.23664の運動量の表現にそれが現れています.これは考え方の不一致では断じてありません.
Re: 斜面の運動
mNeji さんのレス (2009/05/05(Tue) 01:52)
>しかし,現在の高校で物理の授業時間数を考えると私やmNejiさんの時代からしてもとんでもなく圧縮されて,ベクトルも微積分もご存知の通り物理においては中途半端なのです.そして,mNejiさんの表記を読める高校生はよほど優秀で特別な存在だと思います.
だとすると,このような問題を高校生さんに出題する側に大きな責任があるという事を意味します.数学を駆使した授業が出来ないのならば,それはそれで,違う側面で物理を理解する為の問題があってしかるべきでしょう.
小物体に理想的な糸をつけて回転する問題でも,慣性系である直交座標系を使っていれば,高校生さんでなくても解析が面倒になります.所が,糸の中心から見る極座標系を取るだけで,考え方が一変します.これは,問題に適した非慣性座標系(加速座標系)で運動を記述したからです.
所が,この場合でも,極座標のもつ「非慣性座標系(加速座標系)」を不明瞭に提出する為に,「慣性力」という訳の分からん説明に終止しているわけです.今から半世紀ほど前の高校生であった自分も,現在の高校生さんも救われないと思います.
でも,回転系に出て来る極座標のようなツールを必要としない「今回の問題」に,アクロバッティックな慣性力を持ち込み,かつ束縛条件が難解で承服出来ません.この様な説明しか許されないなら,私は論議から撤退するしかないと思う訳です.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/05(Tue) 07:15)
最初の出題の部分で,内容が不足していたことをお詫び申し上げます.
v,Vは,「床に対する」速度と書くのを忘れていました. 本当に申し訳ありません. vは台に対する速度と考えると,確かにmNejiさんの論議にまちがいは ないと思います.
>このような問題を高校生さんに出題する側に大きな責任があるという事を意味します.数学を駆使した授業が出来ないのならば,それはそれで,違う側面で物理を理解する為の問題があってしかるべきでしょう.
仰る通りだと思います. 高校の物理は,微積を用いず公式に代入していくのみですし, ベクトルを用いて考える手法は教えてはいません. 大学で力学を習うとき, 「今まで使ってきた公式は忘れてください.」 と言われたほどです. なので,高校物理に不満をもつことは,自然なことだと思います.
今回は,問題に不備があり,申し訳ありませんでした.
Re: 斜面の運動
Yokkun さんのレス (2009/05/05(Tue) 07:29)
なるほど.「考え方の不一致」というのはそういうことでしたか.ならば,しかたがないのかもしれません.しかし,慣性力を用いなくとも同じであることを私は説明しようとし,なおかつはじめ読み飛ばしたmNejiさんの議論に合わせて展開し始めた所に「考え方の不一致」を出されたものですから,非常に違和感を感じました.
「慣性力」を使うかどうかというのは,それこそ座標系の選択が自由なのと同じで,考え方の自由です.そして,徹底して慣性力を使えば慣性系で書いた運動方程式と何ら変わらない結果を得ることも保証されています.ここに確かに慣性力に対する「考え方の不一致」はあるようです.さらに,私が慣性力を記述に用いたのははじめだけではありませんか.後からは一切慣性系からの記述に終始したはずです.
私は,mNejiさんとのくいちがいはvの読み違いだけだと思っていましたが,どうもそうではないらしい.はじめはそう思って指摘させていただいたのですが,それに対する訂正は重要なことではないと認識されているわけですね.実際mNejiさんの導出においてvの用法さえ変えれば何の変更もいらないことを何度も示唆しているにもかかわらず…この問題とmNejiさんとの「和解」は必ず可能だと確信していたのですが,果たせなくてとても残念です.
#再読すると,vの読み違いと思ったのは私の勘違いで,やはり斜面に垂直な方向をつりあいとみた点がネックになっているように思われました.斜面方向と垂直方向に分けてなおかつ慣性系に固執すると,この問題は途方もない難問に見えます.
Re: 斜面の運動
Yokkun さんのレス (2009/05/05(Tue) 12:22)
ヒノッキーさん,このままお借りしますね. 私としても,このままでは胸のつかえがとれない感じですので,mNejiさんの手法からどう展開すべきだったかについて整理させていただきます.
三角台の運動方程式の 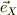 成分から,
成分から,
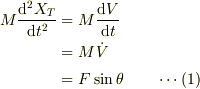
三角台とともに動く座標系では小物体の運動は,
![\frac{\mathrm{d}\vec{X}}{\mathrm{d}t} &= (V+v)\vec{e}_X + u\vec{e}_Y\\ &= (V+v)(\cos\theta\cdot\vec{e}_\theta-\sin\theta\cdot\vec{e}_\perp)+u(\sin\theta\cdot\vec{e}_\theta+\cos\theta\cdot\vec{e}_\perp)\\ &= [(V+v)\cos\theta+u\sin\theta]\vec{e}_\theta+[-(V+v)\sin\theta+u\cos\theta]\vec{e}_\perp](http://hooktail.maxwell.jp/bbslog/3fecf13cb1ebba1ee0782f93f416743b.png)
だから,拘束条件から 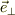 成分はゼロとなるので,
成分はゼロとなるので,
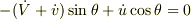
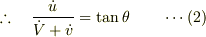
上記座標系は非慣性系だから,この座標系で運動方程式を書くには慣性力を考慮せざるを得ない.
非拘束面( 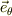 )の方向成分の運動方程式は,
)の方向成分の運動方程式は,
![m[(\dot V + \dot v)\cos\theta+\dot u\sin\theta] = mg\sin\theta+m\dot V\cos\theta](http://hooktail.maxwell.jp/bbslog/95089432a5b183d4c5950ccbef59a98f.png) すなわち,
すなわち,
![m[\dot v \cos\theta+\dot u\sin\theta] = mg\sin\theta\qquad \cdots (3)](http://hooktail.maxwell.jp/bbslog/2ad09b0b3e471c75648ca3def711e711.png) また,
また, 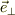 方向の運動方程式は,
方向の運動方程式は,
![m[-(\dot V+\dot v)\sin\theta+\dot u\cos\theta] = mg\cos\theta-F-m\dot V \sin\theta](http://hooktail.maxwell.jp/bbslog/1a85ad9059073e158cc592386c3e6c9c.png) すなわち,
すなわち,
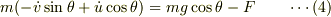 いずれも,「すなわち」の後は慣性系から見た運動方程式に他ならない.
いずれも,「すなわち」の後は慣性系から見た運動方程式に他ならない.
以上(1)〜(4)の4式から, 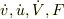 を次のように得る.
を次のように得る.
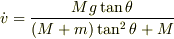
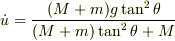
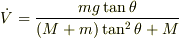
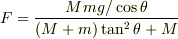
(3)(4)の形から明らかなように,上の小物体の運動方程式は,座標系の回転変換の分だけ冗長になっている.したがって,この運動方程式は水平・鉛直方向に分解して
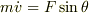
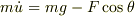 とするのが簡明であった.
とするのが簡明であった.
Re: 斜面の運動
mNeji さんのレス (2009/05/05(Tue) 12:29)
ヒノッキーさん,
>高校の物理は,微積を用いず公式に代入していくのみですし, >ベクトルを用いて考える手法は教えてはいません. >大学で力学を習うとき, >「今まで使ってきた公式は忘れてください.」 >と言われたほどです. >なので,高校物理に不満をもつことは,自然なことだと思います.
理科教育は,退歩しているかのようですね.私の感触では,文科省の図書検定構造が破綻した結果だと思います.
でも考えてみると,高校教育はすでに義務教育の範疇を過ぎているので,生徒さん自らが,必要な勉強をすれば良いのではないでしょうか?
「微積を用いず公式に代入」というのは最早,物理の教育が崩壊しているとしか思えませんね.でも,自分で,微分・積分に親しんでしまえば良いのでしょうね.
また,ベクトルも2次元について把握をすれば,可成りの問題を幾何的に捉えられると思います.その意味では,今回の問題は「ベクトル的センス」を向上する効果があるのでしょう.
>今回は,問題に不備があり,申し訳ありませんでした.
物理の問題を解く上で,「系を記述する座標系」を適切に決めるのがとても大切だと思います.
私は,「問題を見ながら絵にする」ようにしています.とくに力学では,先ず「慣性系座標」を決めようとします.次に,運動を記述するのに適切な相対座標系を探します.往々にして,相対座標系は加速系になることが多いですね.
その次に,運動方程式を慣性系座標のもとで立てます.そののちに,束縛条件などを相対座標によって,束縛面との作用反作用を考慮して決めます.今回の問題は摩擦が無かったので,簡単でしたが....
こうして観ると,『「系を記述する座標系」を適切に決める』のがとても大切なことが実感出来ると思います.
後,問題を解いた後に,「保存量のチェック」とか,「別解の検討」なども時折にでも,されると良いかも知れませんね.
これに懲りずに,確りと勉強を進められますように....
Re: 斜面の運動
mNeji さんのレス (2009/05/06(Wed) 14:28)
●詳細な計算ノート
三角台の置いてある平面の水平方向を 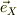 ,垂直方向を
,垂直方向を 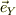 の方向ヴェクタとします.この座標から,三角台の一点Tの座標,
の方向ヴェクタとします.この座標から,三角台の一点Tの座標, 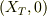 とします.この点から,斜面方向に
とします.この点から,斜面方向に 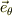 ,斜面に垂直方向を
,斜面に垂直方向を 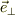 とします.位置ヴェクタと速度ヴェクタ,
加速度ヴェクタを纏めておくと,
とします.位置ヴェクタと速度ヴェクタ,
加速度ヴェクタを纏めておくと,
三角台について,論議の都合上,垂直方向の動きも入れて置くと;
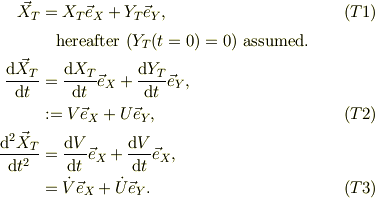
小物体について;
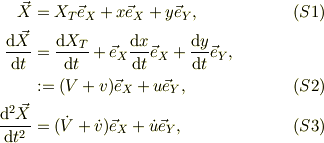
三角台の斜面に沿った方向の単位方向ヴェクタを 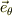 ,斜面に垂直な方向を
,斜面に垂直な方向を 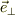 とすると,;
とすると,;
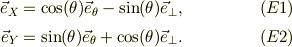
小物体に加わる力には,「重力」と,「三角台の斜面に垂直な抗力F」だけであるから,
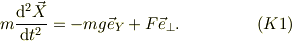
式(S3),(E1),(E2)を用いて, 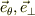 に替えて
に替えて
![[(\dot V + \dot v)\cos(\theta)+\dot u \sin(\theta)]\vec e_{\theta} +[-(\dot V+ \dot v)\sin(\theta)+ \dot u \cos(\theta)]\vec e_{\perp}\\\qquad = -g\sin(\theta)\vec e_{\theta} +[-g\cos(\theta) +\frac{F}{m}]\vec e_{\perp}](http://hooktail.maxwell.jp/bbslog/8fffeb8bcfec93d090e07762264aac88.png)
だから,成分毎の運動方程式として,
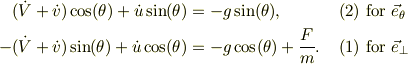
なお,式の番号は,No.23659の式に合わせたので,番号が逆転している.
三角台に加わる力は,小物体に与えた斜面の垂直抗力Fの反作用,と床からの垂直抗力Gとして,運動方程式が得られる.
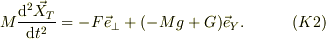
三角台の運動は,床面に接した動きだけだから, 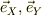 の成分に着目する.
の成分に着目する. 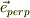 は,式(E1),(E2)から,
は,式(E1),(E2)から,
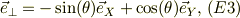
であり,式(T3)とから,
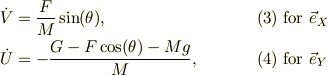
以上,式(1),(2),(3),(4)の4本のが運動方程式である.未知変数は, 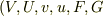 と,6つとなっている.後,2本の式は,運動の束縛面から出て来る.
と,6つとなっている.後,2本の式は,運動の束縛面から出て来る.
先ず簡単なのは,三角台の水平運動の束縛である.運動方向に垂直な方向, 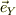 方向の速度
方向の速度  も,その加速度
も,その加速度 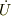 もゼロでないと,この方向に束縛が出来ない.その為には,
もゼロでないと,この方向に束縛が出来ない.その為には, 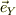 方向の力の総和;式(4)の右辺,がゼロとなる;
方向の力の総和;式(4)の右辺,がゼロとなる;
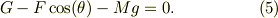
この束縛の結果,床からの抗力が決まり,縦方向の速度が消える事が保証される.
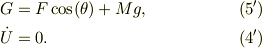
同様に,小物体が斜面上を落下して,斜面から浮いたり,斜面に潜り込まない為には,斜面に垂直な方向, 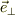 方向の力の総和;式(1)の右辺がゼロとなる;
方向の力の総和;式(1)の右辺がゼロとなる;
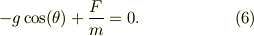
この束縛の結果,斜面から小物体への垂直抗力が決まり,速度間の方程式も決まる;
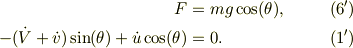
従って,速度の変数, 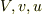 は,式(1'),(2),(3)から求める事が出来る.
は,式(1'),(2),(3)から求める事が出来る.
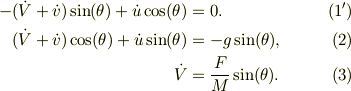
式(3),(6')より,
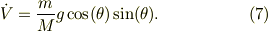
式(1')* ![[-\sin(\theta)]](http://hooktail.maxwell.jp/bbslog/f1d17464fc7cf1b09c60aebbdf97b533.png) +式(2)*
+式(2)* 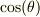 より,
より,
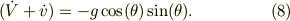
式(1')* 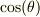 +式(2)*
+式(2)* 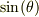 より,
より,

式(8)-式(7)より
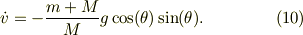
Re: 斜面の運動
mNeji さんのレス (2009/05/06(Wed) 18:54)
●経緯 私の説明が,二つ, No.23652とNo.23655に分かれていて,自分でも検算がし難いので,再度纏めさせて頂きました.座標系は,私自身の混乱を避ける為に,これらと同様にしました.結果は「●詳細な計算ノート:No.23696」に在ります.
通常の力学計算に従った積もりです.自信の無い所は,束縛条件の作り方です.
なお,運動方程式は慣性座標系で立式しました.従って,恣意的な「慣性力」の導入は一切在りません.
★★★★★★★★★★★★★【お願い】★★★★★★★★★★★★★★★★★ ★ ★ア)下記の計算ノートで,考え方や計算で間違いがあれば,ご指摘ください. ★ ★イ)「束縛条件の作り方」について,解り易い本などをご教授ください. ★ ★ウ)この問題か類似問題の回答が明記されている図書などをお教えください. ★ ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
Re: 斜面の運動
Yokkun さんのレス (2009/05/07(Thu) 02:19)
mNejiさん,こんにちは.がんばってますね.本当に頭が下がります.
少しずつ見ていくことにしませんか? まず,問題に(No23650)
>このとき,小物体の鉛直方向の速度の大きさをu,水平方向の速度の大きさをv, 三角台の速度の大きさをVとすると
とありますが,この記述は何もことわりがないので慣性系(床に対して静止した座標系)におけるものであることはお気づきでしょうか?何度か申し上げましたが,mNejiさんの座標と速度 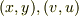 は,三角台に対する相対座標と相対速度としてあつかっていらっしゃいます.しかし,ここですべてを無にするのは惜しいので,mNejiさんの設定に従って議論をすすめようかと思いますがそれでいいですか?
は,三角台に対する相対座標と相対速度としてあつかっていらっしゃいます.しかし,ここですべてを無にするのは惜しいので,mNejiさんの設定に従って議論をすすめようかと思いますがそれでいいですか?
#後段消去しました.
Re: 斜面の運動
mNeji さんのレス (2009/05/07(Thu) 02:52)
Yokkunさん,
他人の解析の精査をされるのも結構ですが,本当に座標系の取り方が本質的に重要ならば,ご自分で運動方程式を立て,必要な拘束条件を出し,それらを基にきちんと解いてください.また,ご自身でお出しになった結果について検算される事をお勧めします.
#私は,どのような座標系を用いても,そのハンドリングが正しい限り,同一の結果になると信じています.
また,運動方程式を書き出しても,恣意的な「慣性力」を導入してしまえば,何の為に運動方程式を作ったのか判らなくなります;最早「物理」ではなくて「空想」になってしまうでしょう.「慣性力」は,自分で車や自転車を運転したり,エレベータに乗ったりしているときは,その実在を体感出来ますが,複雑な系に無批判に導入するのは大反対です.特に,この掲示版は,高校生さん,大学生さんという,初学者の方々がご覧になっているので,恣意的な説明にならないように注意するべきでしょう.
今回の「計算ノート」を丁寧に書いたのは,話の流れを初学者の方々に見て頂きたかったのと,自分の計算の検算でした.
勿論,間違いのご指摘は有難くお受けしますが,部分的な反論よりも,全体像をお示し下さる事を希望します.
Re: 斜面の運動
Yokkun さんのレス (2009/05/07(Thu) 13:59)
申しわけありません.後段は正確ではありませんでしたので,取り消させていただきます.
前段は,よろしいのでしょうか? 前段は明らかに,問題の読み違いだと思いますので,v,u,Vの定義を変えられるならそれを指定してください.v,u,Vは床に対する「速さ」というのが出題のはずです.ヒノッキーさんは,ご自分のミスとして一歩引かれましたが,この部分はmNejiさんの読み違いです.「間違いのみ」指摘させていただきます.ここを解決しないとmNejiさんの努力は報われないと思います.
何度か書いたつもりですが,お求めですので私なりに最良と思われる解き方をまとめます.なお,一般にはベクトル表記の部分は省略されることが多いことを付記します.
床に静止した水平右向き・鉛直上向きの座標系 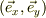 をとる.
この座標系での三角台の座標を
をとる.
この座標系での三角台の座標を 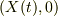 ,小物体の座標を
,小物体の座標を 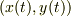 とおく.また,斜面は右に下る方向とする.題意により,
とおく.また,斜面は右に下る方向とする.題意により,
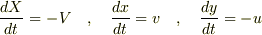 三角台から見た小物体の相対速度は
三角台から見た小物体の相対速度は
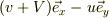 であり,これが斜面下向きであるから
であり,これが斜面下向きであるから
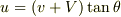 したがってまた,
したがってまた,
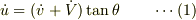
小物体の質量  ,台の質量
,台の質量  とすると小物体の運動方程式は,
とすると小物体の運動方程式は,
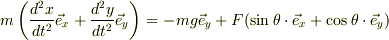 すなわち,
すなわち,
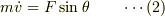
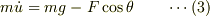 また,三角台の運動方程式は,
また,三角台の運動方程式は,
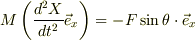 鉛直方向は加速度ゼロなので省略した.
すなわち,
鉛直方向は加速度ゼロなので省略した.
すなわち,
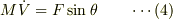 (2)(4)より運動量保存
(2)(4)より運動量保存
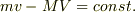 を得る.
を得る.
(1)〜(4)より,…結果は同じでこれで3度目の検算ですのでご勘弁を. 今後mNejiさんの手順に関しては,誤りのご指摘のみにいたします. 失礼いたしました.
なお,慣性力について触れたのは説明の流れから1度のみであって,それ以外に私は慣性力を用いていないのをお気づきなのでしょうか?もちろん,慣性力を用いることはあくまで自由です.むしろ,慣性系と加速系の乗換えをする訓練は,初学者にとって大変有効であると私は思います.これだけは,mNejiさんとは一致しない点です.この類の問題は慣性力を用いるのがわかりやすいと「一般には」いわれています.
Re: 斜面の運動
YUKIA さんのレス (2009/05/07(Thu) 17:46)
今までの一連の流れを見せて頂きました.まずは,この問題が掲載されている図書ですが,『中川の物理講義1(代々木ライブラリー)』のP54にあります.もしかしたら,絶版になっており手に入りにくいかもしれませんが,この問題は大学受験では有名問題なので,一般の大学受験向けの本を探せば見付かると思います.
私も一昨年までは大学受験生で,現在は物理学を専門に勉強していますが,今回の件に関しては, Yokkunさんのご指摘通り,mNejiさんの題意の読み違いが原因だと思います.この問題における速さは,全て慣性系(床に対して静止した座標系)におけるものです.
それと慣性力を導入することについては,それぞれ個人の見解があり,一様に議論することは出来ませんが,私はYokkunさんと同じ立場で捉えています.そもそも,慣性力を導入する理由は,慣性系からの記述では式が煩雑になるからであり,加速系から記述する事でその負担が軽減されるのなら,便利な道具と割り切って使おうという趣旨だと思います.所詮,慣性力は数学的な補正項に過ぎないのですから,無理に物理的な意味付けをしなくても良いのではと思います.
mNejiさんのおっしゃる様に,「慣性力」は,自分で車や自転車を運転したり,エレベータに乗ったりしているときは,その実在を体感出来ますが,これにしても実際は力ではないですしね.人間の感覚に合うということで,「力」という名前がついているだけですから.なので,慣性力が数学的な補正項であることが理解出来る高校生には,便利な道具として使う価値はあると思います.
Re: 斜面の運動
mNeji さんのレス (2009/05/07(Thu) 23:18)
YokkunさんのNo.23704に対して返答いたします.
式については,これから検討します.
>前段は明らかに,問題の読み違いだと思いますので,v,u,Vの定義を変えられるならそれを指定してください.v,u,Vは床に対する「速さ」というのが出題のはずです.ヒノッキーさんは,ご自分のミスとして一歩引かれましたが,この部分はmNejiさんの読み違いです.「間違いのみ」指摘させていただきます.ここを解決しないとmNejiさんの努力は報われないと思います.
これに付いては,途中にヒノッキーさんがNo.23686で,『v,Vは,「床に対する」速度と書くのを忘れていました.』といったご発言があったので承知しています.私の計算が終わった段階で,私の計算結果の「V+v」→「v」にすれば良いだけの話ではないですか.
そういう意味では,私は座標の取り方も含めて,この問題を正確にお聴きしていません.図書もお聴きしましたが,公開出来ないとのお話でした.どうして『v,u,Vは床に対する「速さ」というのが出題のはずです.』と確定的にご存知なのですか?
#このような複雑な問題のばあい,私の様に記憶力の悪い者にとって,「適当に方向を定めるのは混乱のもと」と思います.自在に慣性力を使いこなせる方にとっては細かなはなしでしょうが.
#この経験を活かす意味でも,問題が明確に書かれていないご質問には論議をさけるべきだと知りました.
>なお,慣性力について触れたのは説明の流れから1度のみであって,それ以外に私は慣性力を用いていないのをお気づきなのでしょうか?
その意味では,私は自分の説明に「慣性力」は一切出していません.
私が,Yokkunさんが「慣性力」に関する論議をされていると考えたのは, ・No.23657で,無定義で,「N,A」出て来て, ・No.23658で,ヒノッキーさんが「なるほど,慣性力のmAをすっかり忘れていたので,」 という論議があったので,驚愕しました.
この「A」に関しては,No.23661で,さらに,
>私の立てた運動方程式で説明すると,
> 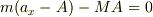 >これを積分するとただちに,
>
>これを積分するとただちに,
> 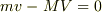 >を得ます.
と,理由不明なまま「-mA」の項が積分すると消滅する一方,「-MA」は残るという不思議な現象を拝見して「?」と思いましたが,あまりにも論議が複雑になりそうなのでそのままにしただけです.その上,直下に
>を得ます.
と,理由不明なまま「-mA」の項が積分すると消滅する一方,「-MA」は残るという不思議な現象を拝見して「?」と思いましたが,あまりにも論議が複雑になりそうなのでそのままにしただけです.その上,直下に
>垂直抗力は, 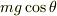 にはなりませんよ.その部分で間違えたのではないでしょうか?斜面に垂直な成分もつりあってはいないのです.つりあいを考えるためには,加速系に乗るわけですから慣性力を落とせないのですね.
にはなりませんよ.その部分で間違えたのではないでしょうか?斜面に垂直な成分もつりあってはいないのです.つりあいを考えるためには,加速系に乗るわけですから慣性力を落とせないのですね.
とお書きになっています.
さらに,No.23691で,
>上記座標系は非慣性系だから,この座標系で運動方程式を書くには慣性力を考慮せざるを得ない.
>非拘束面( 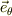 )の方向成分の運動方程式は,
>
)の方向成分の運動方程式は,
> ![m[(\dot V + \dot v)\cos\theta+\dot u\sin\theta] = mg\sin\theta+m\dot V\cos\theta](http://hooktail.maxwell.jp/bbslog/95089432a5b183d4c5950ccbef59a98f.png) >すなわち,
>
>すなわち,
> ![m[\dot v \cos\theta+\dot u\sin\theta] = mg\sin\theta\qquad \cdots (3)](http://hooktail.maxwell.jp/bbslog/2ad09b0b3e471c75648ca3def711e711.png) >また,
>また, 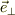 方向の運動方程式は,
方向の運動方程式は,
と,慣性力を恣意的に導入すらされている訳です.
慣性系から加速系に乗り移るばあい,座標変換に従って,自動的に「慣性力」が出て来るのであって,「慣性力を考慮せざるを得ない.」というように,理由が明記されないままに「慣性力」を追加するのはどういうことでしょうか?
一連のご意見を拝見していると,この問題の出典をお持ちなのでは無いでしょうか.もしそうなら,お手数ですが,その問題をご紹介願えませんか?
Re: 斜面の運動
mNeji さんのレス (2009/05/07(Thu) 23:56)
YUKIAさん,情報を戴き有り難うございます.
残念なことに,大学受験の図書を購入する元気がないので悪しからず.
>mNejiさんの題意の読み違いが原因
私は,その問題を未だに全てを存じません.むしろ,今の場合,細かな題意と整合するかどうかは重要でないと思います.逆に,「速度パラメータを正の方向に限定する」方が,私みたいに座標系を一定にとる人間にとっては理解しず来です.
>そもそも,慣性力を導入する理由は,慣性系からの記述では式が煩雑になるからであり,加速系から記述する事でその負担が軽減されるのなら,便利な道具と割り切って使おうという趣旨だと思います.所詮,慣性力は数学的な補正項に過ぎないのですから,無理に物理的な意味付けをしなくても良いのではと思います.
これは,概ねそう思います.むしろ「慣性力」に拘っているのはYokkunさんだろうと思います.
>その実在を体感出来ますが,これにしても実際は力ではないですしね.人間の感覚に合うということで,「力」という名前がついているだけですから.なので,慣性力が数学的な補正項であることが理解出来る高校生には,便利な道具として使う価値はあると思います.
これは冗談ですよね.
小物体を糸につけて回すばあい,我々は小物体が初速度をもって前進しようとするのを,糸が張力によって逐次に方向を変える為に回転する訳です.
もし,我々が,小物体に乗れるとしたら,自分たちが感じる遠心力を糸の張力がキャンセルしているとみますよね.
もし,小物体中で,錘に糸を付けて垂らせば,遠心力によって微小なりとも傾きますし,その力を計測出来ます.
加速系にいる限り,「慣性力」は実在すると思っています.問題なのは「誤解されやすいネーミング」と「使い方を勘違いしやすい点」だと思います.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/08(Fri) 00:52)
長らくこの場から離れていたので,まさかまだ続いていたとは・・・. という状態です.どうもすみません.
え〜と,No.23696について一か所指摘しておきます.
>三角台に加わる力は,小物体に与えた斜面の垂直抗力Fの反作用,と床からの垂直抗力Gとして,運動方程式が得られる.
「小物体に与えた斜面の垂直抗力Fの反作用」とありますが, これは「小物体が三角台を押す力」と表記した方が,正確ではないでしょうか?
さて,ここで問題ですが,
「小物体が三角台を押す力」( 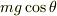 )と
「三角台が小物体を押し返す力」(
)と
「三角台が小物体を押し返す力」(  )は
同じ大きさになるでしょうか?
)は
同じ大きさになるでしょうか?
答えは単純だと思います.
静止または等速運動をしているとき,確かに
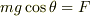 ですが,
今回のように加速度運動をしているときは
ですが,
今回のように加速度運動をしているときは
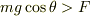 となるはずです.
となるはずです.
この部分,mNejiさんはおそらく,斜面垂直方向にはつり合っているはずだ, と反論すると思いますが,ここがこの問題の罠です.
今回の問題は斜面垂直方向にもつり合っていないのです. No.23674で僕が示しましたが,三角台の運動方程式を, 斜面垂直方向と,斜面方向の運動方程式に書き直してみてください. 斜面垂直方向の力は0ではないはずです.
このように慣性力を用いなくても, 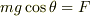 でないことは考えられると思います.
でないことは考えられると思います.
ただ,これでは 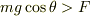 としか表記できないので,
慣性力を持ち込まなければ,運動方程式を記述することは
できないのだと思います.
としか表記できないので,
慣性力を持ち込まなければ,運動方程式を記述することは
できないのだと思います.
単純に 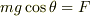 として
ひっかけさせるのが,この問題の目的です.
実際,僕もこの部分にひっかかってしまいました.
として
ひっかけさせるのが,この問題の目的です.
実際,僕もこの部分にひっかかってしまいました.
Re: 斜面の運動
mNeji さんのレス (2009/05/08(Fri) 01:39)
>「小物体に与えた斜面の垂直抗力Fの反作用」とありますが, >これは「小物体が三角台を押す力」と表記した方が,正確ではないでしょうか?
「作用反作用の力」を文章に分散させて見ました.
>「小物体が三角台を押す力」( 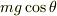 )と
>「三角台が小物体を押し返す力」(
)と
>「三角台が小物体を押し返す力」(  )は
>同じ大きさになるでしょうか?
)は
>同じ大きさになるでしょうか?
ある一つの物体が,PとQとに分裂するような場合,PとQに働く相互作用は,全体としては見えなくなるので,PとQの運動量は保存します.この時,PとQは加速運動をしても善い筈ですね?
もう見ていらっしゃらないと思ったのですが,問題の中で,(V,v,u)の符号の取り方や,斜面の角度の取り方に条件は付かないのでしょうか?それとも,入試問題の場合,暗黙の了解のようなものがありますか?
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/08(Fri) 02:31)
>ある一つの物体が,PとQとに分裂するような場合,PとQに働く相互作用は,全体としては見えなくなるので,PとQの運動量は保存します.この時,PとQは加速運動をしても善い筈ですね?
二人が綱引きをしている状態として考えていきます. mNejiさんの論議は,同じ力で引っ張りあっている状態で, 綱を切断すると,どちらも加速運動をするはずだ, と言い換えてもよいでしょうか?
今考えているのは,綱を切断する前の状態です. (綱を切断するとは,物体を変形させるのと同義) 切断する前は静止か,等速運動をしているはずです.
また,片方の力が強ければ,その方向に加速運動をします. 今回の状況はこちらになるはずです.
>問題の中で,(V,v,u)の符号の取り方や,斜面の角度の取り方に条件は付かないのでしょうか?それとも,入試問題の場合,暗黙の了解のようなものがありますか?
問題によって,正負の向きをきちんと表記しているものや, 絶対値のみを答えさせるものがあります. 今回は後者です.
Re: 斜面の運動
なんとなく さんのレス (2009/05/08(Fri) 03:53)
大体拝見して,もう解決済みかもしれませんが一言. 何か話が輻輳していますが,慣性力を使う・使わないの議論は置いておくとして,又問題の解釈(速度が相対速度か慣性系なのか)などは概ね収束してきたようなので,議論は本質的なところだけで良いのではないかと思います. mNejiさんのNo.2369を検算してみましたが,vが三角台に対する相対速度であれば,mNejiさんも言われているように,v+V→vと見なしてやれば言い訳です. このとき束縛条件は運動方程式とは”別に”u/v=tanθとなります.これはもちろんYokkunさんのu/(v+V)=tanθに代わるものです.そしてNo.2369での束縛条件中のF(式(6))を残したまま,計算を進めると結局,Yokkunさんの計算結果に一致します. これは物体が三角台斜面上に止まる(束縛)条件を慣性系から見た場合,(6)がまずかったのだと思います.u,vは小物体の速度を分解しただけですから,それが斜面の角度と一致する筈で,それと整合します.mNejiさんの立式,計算にそれ以外の誤りはなく,ご本人も自信がないと言われた,束縛条件の不一致があるのみです.他の議論に参加するつもりはありませんが,違いはあまりない気がします.
Re: 斜面の運動
mNeji さんのレス (2009/05/08(Fri) 06:24)
ヒノッキーさん,
>また,片方の力が強ければ,その方向に加速運動をします. >今回の状況はこちらになるはずです.
なにか状況が違うと思います.PとQとの相互作用は消失しますが,それぞれと床の相互作用によって,それぞれは運動を始めると思います.
色々な物体が相互作用して運動する場合でも,個々の部分同士が相互作用するのは2体の相互作用であって;
・多体の相互作用(3つの部分が決まって,初めて相互作用が決まる)は無い. ・個々の部分の加速状態によって相互作用が決まることは無い.
というのが,作用反作用の法則が内包している性質だと思います.恐らく,運動方程式と作用反作用こそがニュートン力学の骨格だと理解しています.
>問題によって,正負の向きをきちんと表記しているものや, >絶対値のみを答えさせるものがあります. >今回は後者です.
なるほど,そうですか.お書きになった文章からはそう思えませんでした.
もしそうならば,No.23660のご発言; >mv+MV=0 >これが運動量保存の式になると思いますが,
は題意に沿っていません.むしろ「後者の立場」なら,「mv=MV」と発想するのが自然でしょう.そこでNo.23664で,
>保存するべき運動量は, 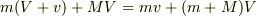 ,だろうと思います.
と申し上げました.
,だろうと思います.
と申し上げました.
私は,細かな表現の違いは後で考えれば良く,むしろ速く問題点を詰めたいだけです.ですから,「題意」とかを強く主張されるならば,問題を正確に示すべきだと思います.そういう意味では,角度の取り方だって,今だ不明です.
Re: 斜面の運動
mNeji さんのレス (2009/05/08(Fri) 06:33)
なんとなくさん,ご意見有り難うございます.
>このとき束縛条件は運動方程式とは”別に”u/v=tanθとなります.これはもちろんYokkunさんの u/(v+V)=tanθに代わるものです.そしてNo.2369での束縛条件中のF(式(6))を残したまま,計算を進めると結局,Yokkunさんの計算結果に一致します. >これは物体が三角台斜面上に止まる(束縛)条件を慣性系から見た場合,(6)がまずかったのだと思います.u,vは小物体の速度を分解しただけですから,それが斜面の角度と一致する筈で,それと整合します.
なるほど,幾何学的な条件の取り込み方はあやふやだったですね.しばらく検討してみます.
>mNejiさんの立式,計算にそれ以外の誤りはなく,ご本人も自信がないと言われた,束縛条件の不一致があるのみです.他の議論に参加するつもりはありませんが,違いはあまりない気がします.
私は,オッチョコチョイなので,ご検討くださって助かります.束縛条件については,もう一度確りと勉強したいと思います.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/08(Fri) 12:12)
>私は,細かな表現の違いは後で考えれば良く,むしろ速く問題点を詰めたいだけです.ですから,「題意」とかを強く主張されるならば,問題を正確に示すべきだと思います.そういう意味では,角度の取り方だって,今だ不明です.
その点につきましては,本当に申し訳ありません. ここに,もう一度問題を記しておきます.
滑らかな床の上に,質量Mの三角台をおく. 斜面と床がつくる角度の大きさををθ(0<θ<π/2)とし, その斜面上に質量mの小物体を置いて静かに離す. このとき,小物体の鉛直方向の速度の大きさをu, 水平方向の床に対する速度の大きさをv, 三角台の床に対する速度の大きさをVとすると, u,v,Vの間に成り立つ関係を表す式を書け.
「〜の大きさをAとする」と書かれたとき, 絶対値で答えることを求められます. これは「暗黙の了解」と言っていいと思います. 問題文でいまだ不適切な部分があるなら指摘をお願いします.
>「後者の立場」なら,「mv=MV」と発想するのが自然でしょう.
おっしゃるとおりです.mv-MV=0が正しい式になります. ここは僕のミスです.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/08(Fri) 12:50)
長くなるので,分けて書きます.
No.23709の論議は大間違いです,どうもすみません.
よく考えると,作用反作用の法則に反したことを書いていました.
「小物体が三角台を押す力」は, 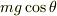 ではありません.
これは
ではありません.
これは  と記述するべきでした.
と記述するべきでした.
ですので,mNejiさんの運動方程式に間違いはありません. 僕の指摘が間違えていました.
問題なのは,小物体が三角台を押す力が,
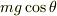 ではなく
ではなく  になるところです.
になるところです.
>なにか状況が違うと思います.PとQとの相互作用は消失しますが,それぞれと床の相互作用によって,それぞれは運動を始めると思います.
確かに綱引きだと,床との相互作用が入ってきて状況が変わってきます. 今回とは状況が変わるので,例えとして挙げるのはおかしかったです
Re: 斜面の運動
Yokkun さんのレス (2009/05/08(Fri) 13:05)
収束に向かうところでの発言は控えようと思いましたが.
混乱の原因がはっきりしたところで,整理しておきたいと思います.
まず,問題の抜き書き(No.23650) 「滑らかな床の上に,質量Mの三角台をおく. 斜面の角度をθとし, その斜面上に質量mの小物体を置いて静かに離す. このとき,小物体の鉛直方向の速度の大きさをu,水平方向の速度の大きさをv, 三角台の速度の大きさをVとすると,u,v,Vの間に成り立つ関係を表す式を書け.」
この問題の範囲で,素直に読む限り紛れは一切ありません. mNejiさんが曲解されたような内容を指定するのならば,最低限後半には次のような表現が必要です. 「三角台の速度をその進行方向を正として水平方向にV,三角台に対する小物体の(相対)速度の水平成分をv,鉛直上向き成分をuとすると,…」
まず,何に対する速度であるかの指定がなければ,静止した床=実験室系に対する速度であると読むのは,ごくあたりまえの表現であると思います.この省略はほとんどの問題において普通になされていることはお認めいただけるのではないでしょうか?
また,あえて「速さ」とは書かずに「速度の大きさ」と書いているのは,ベクトルである速度の大きさすなわち速さであることを強調した表現ですから,これも絶対に読み違える余地のない書き方だと私は思います.
ここにすべての混乱の原因があったことに気付かなかった私は,No.23652,No.23655のmNejiさんの展開の真意を読み取ることができずに,ひとまずそれを無視して(mNejiさんは「別の考え方」として展開されているので)最初の回答者として自分の流れで慣性力を含む運動方程式を立てました.(No.23657)これを受けて不十分な私の記述を読み取ってくれたヒノッキーさんは,No.23654とさらに発展してNo.23658で納得され,またNo.23662にいたって運動量保存まで発展し,質問への回答という目的は3度終わったのです.
さらに継続されたmNejiさんの展開の中で,私はmNejiさんの書かれたものを読み返し,そのときはまだv,u,Vの指定が出題の内容のものであると考えていましたから,mNejiさんは加速系で記述をされておりNo.23659の(1)から正しく束縛条件を導出されたと勘違いし,加速系のまま運動方程式にいたったと曲解をしてその「誤り」を指摘しました.ここはすれちがいになるのは当然で,このあと混乱が続いたまま平行線をたどります.そしてNo.23677〜23678でmNejiさんが相対速度をとられていることに気付き,断言しました.
私がNo.23691で恣意的な慣性力を持ち込んだのは,この混乱をひきずったものです.すなわち,mNejiさんは加速系の座標をとられたまま運動方程式を立てているとの曲解の下,それならば「慣性力」が必要ですよ,とやむなく2度目の慣性力をもちこんだのです.したがって,これはmNejiさんがご自分の速度指定に基づいて厳然と慣性系にのられていることに気付かなかった曲解にもとづくものです.曲解については私の過ちですが,その原因はどこにあったのでしょうか?
『むしろ「慣性力」に拘っているのはYokkunさんだろうと思います.』 上のような経緯をくみとっていただければ,この指摘は的外れのものであるといえます.私は慣性力絶対論者でないことは何度も主張したとおりです.ただし,mNejiさんの排除論とも一線を画する立場ですのでこの点は機会があれば,ぜひ論議したいものです.
お願いしたいことがただひとつあります. No.23714の 「ですから,「題意」とかを強く主張されるならば,問題を正確に示すべきだと思います.そういう意味では,角度の取り方だって,今だ不明です. 」 はNo.23692と同様,いわばお門違いといわざるを得ません.
ここでヒノッキーさんは,「問題の不備」と引かれるでしょう.しかし,運動方程式や加速度の導出まで触れていないヒノッキーさんの問題抜き書きに全く不備はなく,角度の指定を含めて素直に読めば必要十分なものです. 運動方程式の立式以降,すべてmNejiさんがご自分の読み違いのまま始められたことです.ですから,ヒノッキーさんにはこれっぽっちも責任はないのです.
mNejiさんの記述に対する曲解は私のお詫び申し上げるところです. しかし,上のお門違いは私は看過することがどうしてもできません. ここで最低限果たすべき質問・回答の目的と以上の経過を冷静に判断していただきたいと思います.私は曲解はあったものの終始冷静に議論を進めてきたつもりです.そして今後もmNejiさんとはサイト上の楽しい議論を続けていきたいと望むものです.これに懲りずに今後ともよろしくお願い申し上げます.
Re: 斜面の運動
mNeji さんのレス (2009/05/08(Fri) 13:18)
●束縛条件の見直しノート
幾つかの式を見ているうちに,束縛条件を「束縛面に垂直方向の成分=0」とした事は間違えだと思う様になりました.
当初,「角度  の極限で,小物体の束縛と三角台の束縛が同一の条件になる」というのを検算の一つに使えそうだと考えたからです.
の極限で,小物体の束縛と三角台の束縛が同一の条件になる」というのを検算の一つに使えそうだと考えたからです.
今回は,なんとなくさんのご教示; >このとき束縛条件は運動方程式とは”別に”u/v=tanθとなります.
を拝見して,束縛条件とは,
・初期条件として,考察物体が束縛面に接触していて(当たり前か), ・その後の運動速度が束縛面に沿っていること.
と考えると良いのだと思いました.
そこで,小物体の束縛と三角台の束縛条件が;
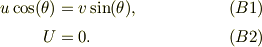
これと,No:23696で得ている,運動方程式群;
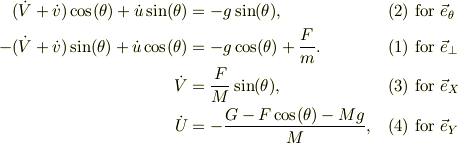
とを連立させて計6本の式から,6個の未知変数, 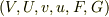 を解く事になる.
を解く事になる.
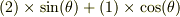 から,
から,
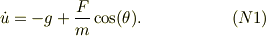
 から,
から,
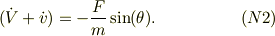
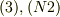 から,
から,
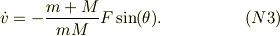
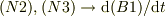 から,
から,
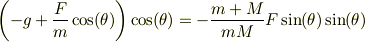
だから,
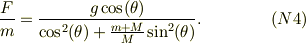
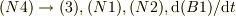 より,
より,
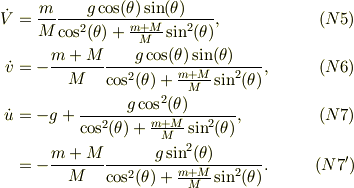
●結果の検討
■小物体の水平方向速度
t=0に静止していて,それから時間がt経過した速度;
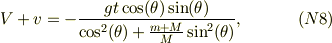
■水平方向の運動量保存 系全体を見ると,外力は垂直方向にだけある.従って慣性系でもた水平方向の運動量は保存する筈である.ちなみに(N2),(N3)からでも,(N6),(N8)からでも
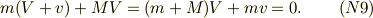
■位置エナジ
小物体の位置エネルギを 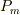 とする.三角台の位置エナジは
とする.三角台の位置エナジは 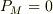 とする.
とする.
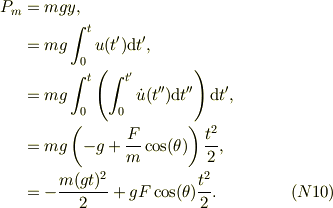
■運動エナジ
小物体と三角台と系全体の運動エナジ,夫々 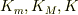 とする;
とする;
![K_m&= \frac{m}{2}[(V+v)^2 +u^2], \qquad\leftarrow (N2),(N1)\\&= \frac{F^2 t^2}{2m} +\frac{m(gt)^2}{2}-gF\cos(\theta)t^2. &\ (N11)](http://hooktail.maxwell.jp/bbslog/773dc6a391cb91b4a4a37c4fa0739f6a.png)
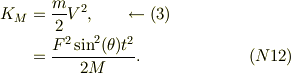
従って,
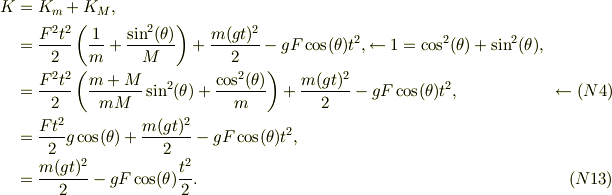
従って,全系の位置エナジと運動エナジの総和は保存する;
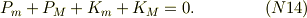
●感想
面束縛の考え方も良く知らなかった私がわるいのですが,こんな難しい問題を高校生さんに「解かせよう」とする出題者さんは何を考えているのでしょうか?
勿論,細かな受験テクニックを駆使して解くと,運動方程式を操作するのは,結構容易なのかもしれません.が,しかし,面束縛までスラスラとでてくる生徒さんが,何れだけ物理的な把握ができるかを「計測」するのに役立つと言うのだろうか??????????????????
Re: 斜面の運動
mNeji さんのレス (2009/05/08(Fri) 14:10)
ヒノッキーさん,
●No.23717について.
問題の再掲くださって,有り難うございます.
私は,大昔の学生ですが,「物理の教科書」や「物理の受験問題」は無視して来たので,非常識の輩です;その意味では,質の悪い説明者でご免なさい.
>「〜の大きさをAとする」と書かれたとき, >絶対値で答えることを求められます. >これは「暗黙の了解」と言っていいと思います.
今後,回答しようとする時に,注意したいと思います.ご教示感謝します.
>問題文でいまだ不適切な部分があるなら指摘をお願いします.
在りません.でも,微積分もヴェクタ計算も禁じられているのに,このような問題を当たり前として出題する側に,強い怒りを持つようになりました.
●No.23718について
>問題なのは,小物体が三角台を押す力が,
> 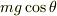 ではなく
ではなく  になるところです.
になるところです.
仰る通りでしたね.なんとなくさんのご教示に従って,再計算中のノート,No.23720を製作中です.そこに,保存側や極限の検討をしたいと思います.
#正に,私自身,大変な勉強をさせて戴きました(大汗).
>確かに綱引きだと,床との相互作用が入ってきて状況が変わってきます. 今回とは状況が変わるので,例えとして挙げるのはおかしかったです
いや,この様な「疑問」をもとに「反論」を繰り出すのは,とても良い論戦の練習だと思います.米国の学生さん達は,日頃の授業でも,教師に質問を繰り出します.恐らく「自分の脳が生みだしたオリジナルの疑問」を機会ある毎に解決していくのが,大局的な理解を育むように感じます.
〜〜〜〜
なお,全体を通して「厳しい言い方」をして来ましたが,大学の同級生との論議,研究室での論議等では,「歳の差」や「学生・教師の違い」は問題でなく,お互いに自分の信じる所を主張し,説明する態度が重要だと思います.
今回のように,「高校生さん」との論議といえども,自分の見解を論じる相手と考えて書かせて頂きました.これに懲りず,多いにアイデアを磨かれます様に.
Re: 斜面の運動
mNeji さんのレス (2009/05/08(Fri) 23:03)
YokkunさんのNo.23719について申し述べさせて頂きます.
今回の一番の食い違いは, ・座標の設定 ・束縛条件の付け方,表記のしかた. ・運動方程式 などにあったとおもわれます.
現在, No.23720で「束縛条件の見直しノート」を製作中です.自分の意見は,そのように変更しました.座標の取り方は食い違ったままですが,結果はYokkunさんの結果と同類だろうと思います.
私の計算には慣性力の論議は皆無なので,これ以上,慣性力の論議は差し控えたいと思います.
束縛条件の考え方は,初めて知りました.ご教示,有り難うございました.
Re: 斜面の運動
ヒノッキー さんのレス (2009/05/11(Mon) 01:04)
mNejiさん,No.23720の解答,拝見しました. 慣性力を用いなくても解けるということに 納得いたしました.
>面束縛の考え方も良く知らなかった私がわるいのですが,こんな難しい問題を高校生さんに「解かせよう」とする出題者さんは何を考えているのでしょうか?
ここまで導出していただいたのに,ケチをつけるようで悪いのですが, 今回の問題はv,u,Vの関係式を求めるだけなので,(B1)の時点で, 答えはでています.
しかし,この内容だけでもu,v,Vを求めることができる ことは大変勉強になりました.
>今回のように,「高校生さん」との論議といえども,自分の見解を論じる相手と考えて書かせて頂きました.これに懲りず,多いにアイデアを磨かれます様に.
僕もいろいろな意見を聞けて楽しかったです. ・・・あと実は,大学生です. 高校生を教えている際にこの問題が出たので, ここに助けをもとめにきました.(冷や汗)
mNejiさん,Yokkunさん,YUKIAさん,なんとなくさん, どうもありがとうございました.