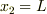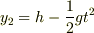物理初心者 さんの書込 (2009/05/01(Fri) 21:39)

矢から木までの距離をL，木の高さｈとして， 木の上にいる猿を射止めようとして，猟師が矢を発射した．猿は矢が発射された瞬間に気づいて，枝から手を離して自由落下を始めるとする．この猿を射止めるには矢の発射角度をどのようにすればよいか．（角度θまたはL対hの比で答えなさい） ただし，矢は斜めに投げた物体の運動と同様の運動をするものとする．

全くわからないので詳しい解説お願いします．

Yokkun さんのレス (2009/05/01(Fri) 21:58)

こんばんは．

モンキーハンティング問題といいます．「答え」だけなら，次のシミュレーションを見てもらえばわかります．

> http://www.youtube.com/watch?v=9OB-vqsb8aQ 

が，もちろん「答え」だけでは困りますよね？ この問題には「相対性原理」という深奥な基本原理が潜んでいるのですが，それはさておき．

「自由落下」と「斜方投射」の問題ですので，矢と猿の運動を式に書けなければなりません．通常，矢の発射位置を原点にとり，木に向かって水平方向に 軸，鉛直上方に 軸をとるのですが，初速 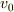として時間 の後の矢の位置 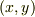を与える式が書けますか？

物理初心者 さんのレス (2009/05/01(Fri) 22:26)

t秒後の矢の位置は（v₀cosθｔ, v₀sinθｔ-1/2gt＾2）でOKですか？

物理初心者 さんのレス (2009/05/01(Fri) 22:30)

t秒後の矢の位置は（vo cosθｔ, vo sinθｔ-1/2gt＾2）でいいですか？

Yokkun さんのレス (2009/05/01(Fri) 22:31)

大丈夫のようですね．書き直しますと，

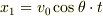
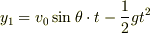
猿の位置と区別するために添字1をつけました． さて，時間 の後の猿の位置はどう書けるでしょうか？

物理初心者 さんのレス (2009/05/01(Fri) 22:35)

t秒後の猿の位置はy=gtでいいですか？

Yokkun さんのレス (2009/05/01(Fri) 22:36)

おっと．それは，t秒後の速さですね．

物理初心者 さんのレス (2009/05/01(Fri) 22:40)

あ... y=1/2gt＾2ですね？

Yokkun さんのレス (2009/05/01(Fri) 22:51)

はい．ところで，矢が猿に命中するということは両者の座標がある時刻に一致するということです．しかし，同じ座標軸で位置を表さないと判定できませんね？猿のt秒後の位置を矢と同じ座標軸で示してください．

物理初心者 さんのレス (2009/05/01(Fri) 22:58)

ｔ秒後の矢と猿のｙ座標が等しいから vo sinθｔ-1/2gt＾2 = -1/2gt＾2 ↑が成り立つみたいな感じでいいですか？

Yokkun さんのレス (2009/05/01(Fri) 23:07)

>vo sinθｔ-1/2gt＾2 = -1/2gt＾2

みたいな感じなのですが，猿の位置が違いますね？地面の下になってしまいます．t=0で猿はどこにいるのでしょうか？ あと，猿の水平位置（x座標）はどうですか？

物理初心者 さんのレス (2009/05/01(Fri) 23:09)

vo sinθｔ-1/2gt＾2 = ｈ-1/2gt＾2 ですね？

物理初心者 さんのレス (2009/05/01(Fri) 23:11)

猿の水平位置はLだから 矢と猿のｘ座標の関係は vo cosθｔ= L ですか？

Yokkun さんのレス (2009/05/01(Fri) 23:14)

両者の座標が一致するから，水平位置の比較からtが求まり，鉛直位置の比較でθが得られるはずです．

物理初心者 さんのレス (2009/05/01(Fri) 23:27)

水平位置の関係式から ｔ＝L/vo cosθ が出てきて 鉛直の関係式にtを代入して整理すると hcosθ = Lsinθ となってｈとLが邪魔でθが求められませんが・・・

Yokkun さんのレス (2009/05/01(Fri) 23:29)

hとLは与えられているのですから，当然θの式に含まれていいのですよ． θをh，Lの式で表せばそれが答えです．

物理初心者 さんのレス (2009/05/01(Fri) 23:38)

hcosθ = Lsinθ この式からθを求めるやり方がわからないのですが・・・

Yokkun さんのレス (2009/05/01(Fri) 23:40)

両辺を 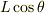で割ってください．

物理初心者 さんのレス (2009/05/01(Fri) 23:45)

tanθ＝ｈ/Lまででました． この後はどうするんでしょうか？

Yokkun さんのレス (2009/05/01(Fri) 23:50)

それで終わりです．

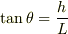または， （ ）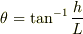

猿にまっすぐ向かって矢を放てばよいのですね．この結果は，少なくとも次の２つの解釈が可能です．

1. 猿にまっすぐ向かう矢の初速度 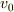と同じ速度で矢にくっついていく実験室を考えると矢は実験室内で初速ゼロで自由落下する．実験室が猿の位置まできたとき，同様に自由落下した猿と同位置になるのは当然である（相対性原理＝等速度で運動する実験室で起こる現象は静止した実験室で起こるものと何ら変わりがない）．
2. 矢と猿を含む大きな実験室を一緒に自由落下させると，実験室内は無重力である．したがって，この実験室内では矢は猿に向かってまっすぐ等速度運動をする．

以上のような解釈に立てば，実は計算をしなくても結果がわかるということは知っておいてソンはないでしょう？

物理初心者 さんのレス (2009/05/01(Fri) 23:58)

θを出す時にまさか昨日数学で習ったアークタンジェントを使うとは・・・

とてもわかりやすい解説ありがとうございました！！ you-tubeのシュミレーションはとてもよかったです！ 最後の解釈ノートにメモらしていただきます！m(_ _)m

物理初心者 さんのレス (2009/05/01(Fri) 23:59)

時間遅いですがもう一問質問いいですか？

Yokkun さんのレス (2009/05/02(Sat) 00:00)

いいですよ．明日は用事があって早いのですが，どうせお休みですから．