ベクトルの右手系
ベクトルの右手系
数学迷い人 さんの書込 (2009/04/30(Thu) 10:07)
ベクトルa=(3,-1,-2),ベクトルb=(2,-3,1)とします.
ベクトルa,bに垂直な単位ベクトルnで,{a,b,n}が右手系になるものを求めよ.
ということですが,どういうことですか?
右手系に関しての定義はわかったのですが,問題になると,どう手を着ければいいのかわかりません.この例題の解き方手順を教えてください.
Re: ベクトルの右手系
toorisugari no Hiro さんのレス (2009/04/30(Thu) 10:19)
瞬間的な計算方法もありますが,それをいきなり教えてもあなたのためにならないので,違う方法で誘導します.
求めるベクトル 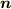 に平行なベクトルを
に平行なベクトルを 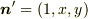 とおきます.
とおきます.
- 「ベクトル
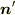 はベクトル
はベクトル 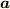 に垂直」を式にしてください.
に垂直」を式にしてください. - 「ベクトル
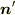 はベクトル
はベクトル 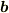 に垂直」を式にしてください.
に垂直」を式にしてください. - 連立方程式を解いて,
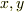 を求めてください.
を求めてください. 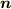 は単位ベクトルであることから,
は単位ベクトルであることから, 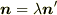 となる
となる  を求めてください.ただし,2通りあります.
を求めてください.ただし,2通りあります.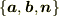 が右手系になるように
が右手系になるように  を一意に決定して,
を一意に決定して, 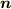 をもとめてください.
をもとめてください.
ま,(5)はきびしいから(4)まではできて欲しいです.
Re: ベクトルの右手系
数学迷い人 さんのレス (2009/04/30(Thu) 11:12)
最初に,(1,x,y)と置いていますが,(x,y,1)とおいたりしても良いのでしょうか?
n’=(1,1,1)となりました.
そして,λ=±(√3)/3となりました.
?の決め方がよく理解できないです. n=±(√3)/3,(√3)/3,(√3)/3)まではわかりました.
Re: ベクトルの右手系
数学迷い人 さんのレス (2009/04/30(Thu) 13:09)
それとすいませんが,次の問題で,
ベクトルo,a,bを含む平面上にu=(1,2,1)を正射影したベクトルを求めよとのことですが,,,,.
ベクトル上への正射影なら,cosを使って計算できたのですが,この場合それは使えないですよね?ヒントを頂けないでしょうか?
Re: ベクトルの右手系
toorisugari no Hiro さんのレス (2009/04/30(Thu) 13:27)
> 最初に,(1,x,y)と置いていますが,(x,y,1)とおいたりしても良いのでしょうか?
(1,x,y)で解が存在しない場合は(x,y,1)あるいは(x,y,z)とおきます.
右手系を判断するのは,外積が必要です.それだったら,次のステップにいきましょう.
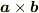 および
および 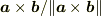 を求めてください.
を求めてください.
> ヒントを頂けないでしょうか?
平面に垂直なベクトルは分かりますか?
Re: ベクトルの右手系
数学迷い人 さんのレス (2009/04/30(Thu) 13:43)
a×b/|a×b|=1/√3(-1,-1,-1)となりました. これが,求めるnベクトルということですか?もう少し理由をお願いいたします.
内積が0と,法線ベクトルという言葉くらいしか思いつきません.
Re: ベクトルの右手系
mNeji さんのレス (2009/04/30(Thu) 15:33)
横から失礼します.
>a×b/|a×b|=1/√3(-1,-1,-1)となりました. >これが,求めるnベクトルということですか?もう少し理由をお願いいたします.
三つのベクトルをxyz座標に作図して,それぞれの相対関係を掴めませんか?
Re: ベクトルの右手系
toorisugari no Hiro さんのレス (2009/04/30(Thu) 19:47)
> もう少し理由をお願いいたします.
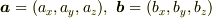 として,
として, 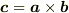 の成分を計算してください.
の成分を計算してください.
そして, 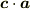 ,
, 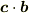 を計算し,そこから何が言えるかを考えてください.
を計算し,そこから何が言えるかを考えてください.
ヒントが
> ベクトルo,a,bを含む平面上にu=(1,2,1)を正射影したベクトルを求めよとのことですが,,,,.
についてのことなら絵を描いて考えてみてください.
Re: ベクトルの右手系
数学迷い人 さんのレス (2009/05/01(Fri) 09:58)
もちろん図を描いてみました.けれども,,,. xy,yz,zx面でそれぞれ考えるのでしょうか?
Re: ベクトルの右手系
mNeji さんのレス (2009/05/01(Fri) 13:17)
>もちろん図を描いてみました.けれども,,,.
今後も困ったら,絵を書くといいと思います.段々と慣れますから.
>xy,yz,zx面でそれぞれ考えるのでしょうか?
でも,そこまで細かくは判らないですね.高校生の時に,右ネジの法則とかいって,右手で直交座標を作ったと思います.この調子でいえば, 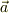 を中指の向き,
を中指の向き, 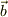 を親指の向きとした時に,
を親指の向きとした時に, 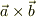 が人差し指の向きになるかどうかを調べてみたら?
が人差し指の向きになるかどうかを調べてみたら?