光太郎 さんの書込 (2009/04/23(Thu) 13:56)

こんにちは． 学部4年の光太郎といいます．

大学院の過去問を解いていたら，分からない問題が出できたのでみなさんのお力をかりたく相談に来ました． 以下問題です．

長さ1(m)の棒の一次元熱伝導を考える．時間をt(s)，棒の一次元座標をx(m)とする．初期状態において棒の温度Tは一様に0(℃)である．t=0(s)で，棒の左端の温度が瞬間的に50(℃)に引き上げられ，その後は，その温度で維持される．棒右端の温度は0(℃)一定である．次の一次元の熱伝導方程式を用いて以下の問いに答えよ．

∂T/∂x=a^(2)∂^(2)u/∂x^(2)

(問) T(x,t)=A(x)B(t)と置き，二つの常微分方程式に変換しなさい． また，与えれられた境界条件と初期条件の下で解きなさい．

という問題です．

分からない点 ?境界条件がT(0,t)=50，T(1,t)=0となっていてx=1の時の温度が50℃なので， A(0)が求まらず，先に進めない．

つまり，一つの常微分方程式はA"=kAで， kの値は(i)k=p^2>0 (ii)K=-q^2<0 (iii)K-0 の三つに分かれるが，決定することができない．

?初期状態の状況が分からない．問題文から初期状態では棒では一様にT=0． つまり，xがどこでもT=0．しかし，t=0の時，棒の左端の温度を50℃にすると書いてあるので，t=0において棒では一様に0℃ではないということになる． 自分は初期条件というのは，t=0の時だと思っていたので，混乱してしまいました．

長くなりましたが，よろしくお願いします．

なんとなく さんのレス (2009/04/23(Thu) 17:04)

光太郎さん，こんにちは． 思ったことだけで申し訳ないですが，ヒントになれば． まず，方程式は，∂T/∂t=a^2∂^2T/∂x^2の間違いですね． 問題文を注意深く読むと，t<0で定常状態，t=0で左端(x=0)に瞬間的に50℃の熱浴接触，それを維持したまま右端(x=1)を0℃に維持する．と読めます． お書きのように変数分離を適用しますが，境界条件からk=-p^2(p>0)の解だけ考慮すれば良いでしょう．しかし，これは結合定数だけの調整では上手く行かないと思います．なぜなら，変数分離解は，左端に瞬間的な与熱が伝わり右端にまで到達する過渡的現象と左端が50℃，右端0℃になった後の定常的状態を一度に表現出来ないからです． 言い換えると，その境界条件は（t=0を除いて）tがある程度経った後に実現されるものだと思います．物理的に考えれば，定常状態（時間によらない）ではx方向の温度勾配は一定の解を持つと思います．したがって，この問題の解はそのような定常解と過渡的（境界条件T(0,0)=T(1,0)=0)の重ね合わせになるのではないでしょうか．過渡的解は速やかに収束する筈です．

ASA さんのレス (2009/04/25(Sat) 08:19)

補足しておきます． k=0;A(x)=ax+b,B(t)=1;t=0でB=1にノーマライズ これが，"左端が50℃，右端0℃になった後の定常的状態"の解を示してます． k<0;A(x)=αexp(ikx),B(t)=exp(-νt) これが過渡的解で，後は境界条件を満たすためのフーリエ展開係数を求める問題に帰着しますね．

toorisugari no Hiro さんのレス (2009/04/25(Sat) 20:16)

> 後は境界条件を満たすためのフーリエ展開係数を求める問題に帰着しますね．

まあ，そうだけど，簡単ではないですね．

区間を2倍にして，反対称に拡張して 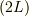周期関数化した(同次解の)初期条件

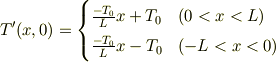
のフーリエ変換から導かれる

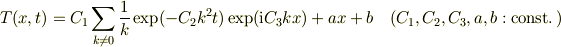
という楽しい計算をする羽目になると思うのだけど．(特異な初期条件だから難しい．)

mNeji さんのレス (2009/04/25(Sat) 22:00)

光太郎さん，拡散型の微分方程式は私も苦手です．

toorisugari no Hiroさん， ＞周期関数化した(同次解の)初期条件 これには賛成ですが，

この初期条件のような先見的な設定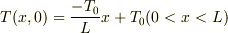； ＞ が理解出来ません．

私としては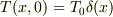， みたいな感じを受けています．なにしろ，t=0までは全体は０℃に保たれていた訳ですから．

ASA さんのレス (2009/04/26(Sun) 10:41)

>簡単ではないですね． 基本的問題だと思います．方針としては，フーリエ展開だから， [0,π]の区間に拡張して考えてます． 初期状態は，下にとがった過渡的三角波が最終状態のくだり勾配を打ち消しているためフラットな状態でいると考えればよいはず． 最終状態T(x,∞)=50(-x+1)なので，打ち消し関数として係数除いたf(x)=x-1を公式に入れてsinの展開係数Cnを計算すると，たぶん-B/n． T(x≠0,t)=-B?(sin(kx))/n)exp(-(ak)^2)-50x+50，k=nπ,B>0(2とかπとかT0=50からなる) T(0,t)=50 これが答えだと思う． x=0は特異点なので，x=0を分けて考えるのがミソかも． (δ関数とか変なの持ち出しちゃいけませんよ)

なんとなく さんのレス (2009/04/26(Sun) 11:13)

スレ主さんが出てこられないので進めるのはどうかと思っていたのですが，ここまで議論が進んでしまったので総括してひとつの解答例を示し，皆さんの御意見をお聞きしたいと思います．まあ，早く言えばこれでいいのか？という疑問があるわけですが． すでに指摘されたようにt→∞における漸近解， 定常解T1(x,t)〜50(1-x) が得られます．一方，境界条件T(0,t)=T(1,t)=0と変数分離法により， T2(x,t)=ΣBnexp(-(naπ)^2t)sin(nπx) が考えられますが，周知のように一般的にはこのBnが初期条件f(x)のフーリエ展開係数に一致するようにします．ところがmNejiさんが疑問に思われたように，この初期条件がT0δ(x)のような接触であるため工夫が要ります．発想を転換し，初期条件をx=0以外でほとんど至る所0，つまりT(x,0)〜0とすれば，T=T1+T2=0より，T2=-T1，f(x)=-T2=-50(1-x)とすれば原点以外ほぼ０のフーリエ変換となると期待されます．そこで，Bn=-100∫_{0,1}(1-x)sin(nπx)dx=-100/(nπ)と置くことにより， T(x,t)=-100Σexp(-(naπ)^2t)sin(nπx)/(nπ)+50(1-x) を解として得ます． 結果的にδ関数の再構成の気もしますが，数学的に厳密でないので私にはこれが精一杯ですね． しかし，これが院試だとすると，時間内にこれだけの考察ができるのだろうか？ちょっと疑問です．

toorisugari no Hiro さんのレス (2009/04/26(Sun) 13:20)

> 私としては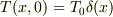， みたいな感じを受けています．なにしろ，t=0までは全体は０℃に保たれていた訳ですから．

フーリエ成分が拡散方程式に従って変化したとき，境界条件を常に満たせるようにできますか?

mNeji さんのレス (2009/04/26(Sun) 14:34)

＞フーリエ成分が拡散方程式に従って変化したとき，境界条件を常に満たせるようにできますか?

x=0で条件を満たすと，x=Lで0℃にキープ出来ない様ですね．

＃フーリエ展開には，いつも焦れてしまいます． ＃老人になって，漸く冷静に問題に対面出来る様になりました(笑)．

自分としては，初期条件に基づいて拡散方程式の解を求め，その時間を十分長くすると，高次のフーリエ成分から急速に落ちて行き，最後に直線的な解が残るというのを想定していました．が，こういうナイーブな流れは無理なのでしょうかね？

toorisugari no Hiro さんのレス (2009/04/26(Sun) 16:27)

> 初期条件に基づいて拡散方程式の解を求め，その時間を十分長くすると，高次のフーリエ成分から急速に落ちて行き，最後に直線的な解が残るというのを想定していました．

間違っていません．ただ，境界条件を何に満足させるか (1) フーリエモードを逆変換した関数が満足する(おのおのはみたさなくてよい)． (2) 漸近解を分離して，残りはすべてのモードでディリクレ条件(境界で0)を満たす． の二つの方法のどちらかを選択しないといけません．

後者なら，この問題の境界条件では，フーリエモードは奇関数(sin関数)成分のみになってしまいます．

ただ，フーリエ変換自体が正しいのかはよく分かりません．この手の境界条件の問題はチェビシェフ展開＋(1)で解くのが普通ですから． # 境界における熱流( 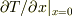)がフーリエ変換では正しく評価されないんじゃなかったっけ．(それについては良く知らないから聞かないで．) # チェビシェフ展開でどう計算するかも良く知らないから聞かないで．

光太郎 さんのレス (2009/04/27(Mon) 17:05)

こんにちは．

コメントが大変遅くなってすいませんでした． みなさまのコメントありがとうございます．とても参考になります．

みなさまのご指摘の通り 新しくT2(x,t)=T(x,t)-T1(x,t)=T(x,t)＋50(x-1) という関数を導入すれば，うまく境界条件を使え， T2(x,t)=ΣBnexp(-(naπ)^2t)sin(nπx) となります．

ここで疑問なのですが，問題文を見ると 「T(x,t)=A(x)B(t)と置き・・・」と指定されているので， T2(x,t)という関数を導入することなく解けということじゃないかと思います． しかし，T2(x,t)を導入しなきゃ解けないと思うのですが，T(x,t)=A(x)B(t)と 置いてからうまくT2(x,t)を導入する方法はあるのでしょうか？

なんとなく さんのレス (2009/04/28(Tue) 00:12)

なんとなくです． 既出であり，大した話ではありませんが．．． 変数分離の際に，A∂B=B∂^2Aとなる訳ですが，∂^2A=∂B=0の場合があります． このとき，B=定数，A=C1x+C2ですから，T=Cx+Dが特解であることが出てきます． したがってASAさんやhiroさんが最初に書かれた式のように，この項は変数分離から出てくるもので，フーリエ解とは明らかに独立ですから，一般に結合した解を得られます．後は初期（境界）条件の問題に帰着するのでしょうね．

mNeji さんのレス (2009/04/28(Tue) 01:50)

なんとなくさん，

＞この項は変数分離から出てくるもので，フーリエ解とは明らかに独立ですから，一般に結合した解を得られます．

変数分離の常数項は，空間の微分方程式の固有値問題として与えられる訳です．そして，その固有関数が「有限領域に限定される」という事から固有値は負で，かつ離散的になります．微分方程式の解としての固有関数が，フーリエ級数と一致しているのではないでしょうか．

従って，変数分離で得た固有値解の和にも，直線的な「Cx+D」は含まれている様に思いますが？

ASA さんのレス (2009/04/28(Tue) 07:07)

>変数分離の常数項は，空間の微分方程式の固有値問題として与えられる訳です． 時間の1階微分方程式の問題と見ることもできます． 時間的な条件によって，3タイプ(増大，定常，減衰)の結合を選択すると考えます．(ある有限の時間，熱源を接触させた場合などは増大解を選択します．）

mNeji さんのレス (2009/04/28(Tue) 09:58)

ASAさん，

＞時間の1階微分方程式の問題と見ることもできます． ＞時間的な条件によって，3タイプ(増大，定常，減衰)の結合を選択すると考えます．

この可能性はありますね．でも今回の場合だと，時間的には，定常(n=0)と減衰(|n|>1)だけが許されるのだと思います．そうでないと，有限領域にのみ起こっている現象にならない，簡単に言ってしまえば「空間的に，周期解にならないで，指数関数的な増減解になってしまう」，と思うのですが．

＞(ある有限の時間，熱源を接触させた場合などは増大解を選択します．）

この場合，空間的には無限な系ではありませんか？その事例がある図書とかウェブ・サイトをお教え下さると嬉しいです．

ASA さんのレス (2009/04/28(Tue) 12:44)

mNejiさん

何か勘違いなされているような気がします． >空間的には無限な系ではありませんか？ 空間的な広さとは無関係ですよ．単純な例として，熱の逃げ場がないケースを考えると，境界条件として∂T(x=0,anytime)/∂x=0になります．これを満たす時間的増大解の空間関数としてはT(x)=T0cosh(kx)があります． でこれは，区間の大きさにかかわらず成立します(初期状態は，フラットではないが)． これは，x=Lにある熱源を接触させている期間，系の温度が時間と共に増大する例を示しています． 初期の温度分布や注入熱量を上の例と別のものにすれば，それに応じて他の要素がmixされます（もっとも，条件によっては，変数分離解だけでは表現できないケースもあるでしょうけども）．

mNeji さんのレス (2009/04/28(Tue) 13:29)

ASAさん，

＞何か勘違いなされているような気がします．

今までも，拡散型の微分方程式を明快に理解出来なくています．ですから，この問題を切っ掛けにして勉強させて貰っています．

ご説明の問題はまだ理解出来ませんが，検討させて頂きます．

mNeji さんのレス (2009/04/29(Wed) 12:59)

すこしだけですが，自分の過ちに気づいたのでコメントします．ただし，皆様のお書きになった範疇の事だと思います．

大きな間違いは，「変数分離型の解によって，初期条件も，時間が十分に経過した定常解(変な言い方かも知れませんが，終期解といった方がイメージしやすいかも)も表現できている筈」という点だろうと思います．

解くべき拡散方程式は，

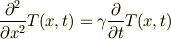
ですが，左辺のラプラス方程式に，右辺の外力項が加わったポアソン方程式と成ったと見る事も出来ます．当然，終期解はラプラス方程式を満たし，拡散方程式の特解に加える事もできます．

もう少し具体的に理解出来るまで，考えたいと思います．