ヒノッキー さんの書込 (2009/04/22(Wed) 18:08)

長文失礼します 統計力学の問題で，納得できない解法があったので， 力を貸してもらいに来ました 内容自体は高校内容です

ミクロカノ二カル分布の問題です

Ｎ個の原子が規則正しく並んで完全結晶を造っている このうちｎ個（Ｎ＞＞n＞＞１）個の原子を 格子点から表面に移すとき，格子欠陥が生じて不完全結晶になる． このとき，n個の欠陥の配置の仕方の数，Ｗ（ｎ）を求めよ

僕は，Ｗ＝ＮＣｎとして解いたのですが，（Ｃはコンビネーションです） 答えは，Ｗ＝（Ｎ＋ｎ）Ｃｎとなっていました 先生に聞いたところ，Ｎ，ｎは大きいのでどちらでもいいが， 答えのほうがより正しいと言っていました． その理由は表面の欠陥を考える必要があるそうです． しかし，移したときに欠陥が生じたのだから， 表面に欠陥がある，と考えることがよくわかりません．

なぜ，表面の欠陥を求める必要があるのか，教えてください

Yokkun さんのレス (2009/04/22(Wed) 18:55)

あまり得意な分野ではないですが（というか苦手な分野ですが）

>このうちｎ個（Ｎ＞＞n＞＞１）個の原子を 格子点から表面に移すとき，

とありますが，移った原子も相変わらず結晶の構成の一部なのではないですか？ すると，全部でN+n個の格子点から欠陥を選ぶことになると思います．

ヒノッキー さんのレス (2009/04/22(Wed) 19:13)

返信ありがとうございます

＞全部でN+n個の格子点から欠陥を選ぶことになると思います．

例えば，表面に一つ欠陥があるとしたとき，それは（nー１）個 を動かしたときの配置になると考えてしまうのですが， それではいけないのでしょうか？

Yokkun さんのレス (2009/04/22(Wed) 21:11)

あまり知識のないところで単純に回答している点，お許しください．

問題の主旨は，あくまで原子数は 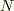，欠陥数が である場合の数を求めるというふうに解釈できるかと思うのですが，いかがでしょうか？すなわち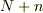， 個の格子点により結晶が構成されていて，そのうち 箇所に欠陥が存在すると考えるのだと思います．

ヒノッキー さんのレス (2009/04/22(Wed) 21:57)

なるほど・・・大分，イメージをつかめました

実際，移動した原子が何個で何処にあるのかわからないから， 移動の際にできた欠陥を探すよりも， 移動した後の結晶構造（訂正：格子点の数）を決めつけて，欠陥を探す方が簡単だ， という感覚でしょうか？

後出しで申し訳ありませんが，問題ではこのあと ｎ個を表面に動かすときのエネルギーを Ｅ＝ｎε としてＷ（Ｅ）であらわせと続きます．

このとき，表面に欠陥がある時とない時は 同じエネルギーではないが，Ｎ＞＞ｎより 表面に欠陥ができる配置はとても少なく，無視できる， と考えればいいのですね