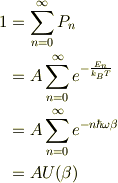光子のエネルギー平均値の計算
光子のエネルギー平均値の計算
えり さんの書込 (2009/04/19(Sun) 20:57)
以下の問題の計算途中で,止まってしまいました.
「角振動数ωの光子はエネルギー 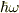 をもつ粒子として振舞う.n光子状態のエネルギーは
をもつ粒子として振舞う.n光子状態のエネルギーは 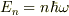 となる.温度Tのときn光子状態の統計的確率は
となる.温度Tのときn光子状態の統計的確率は 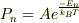 となる.
(a)n=0,1,2…の全確率が1になるように規格化因子Aを決めなさい.
(b)角振動数
となる.
(a)n=0,1,2…の全確率が1になるように規格化因子Aを決めなさい.
(b)角振動数  の光子のエネルギーの平均値
の光子のエネルギーの平均値 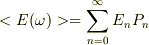 を求めなさい.
…」
を求めなさい.
…」
という問題で,解いてみたら
(a)は 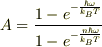 となり,
(b)は
となり,
(b)は
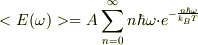 ここで
ここで 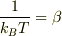 とおくと,
とおくと,
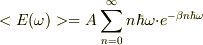 また,
また, 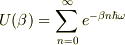 とおくと,
とおくと,
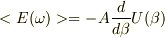
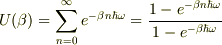
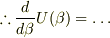 となったのですが,すごく複雑な結果になりそうな気がするのと,もっとスマートな計算のしかたがあるような気がしたので投稿させていただきました.シグマをインテグラルで書き換えても大丈夫なのでしょうか?また,その場合は0から∞で積分しなくてはいけないのでしょうか?個人的にガウス積分を使いたいので,-∞から∞で積分したいのですが…
教えてください.宜しくお願いします.
となったのですが,すごく複雑な結果になりそうな気がするのと,もっとスマートな計算のしかたがあるような気がしたので投稿させていただきました.シグマをインテグラルで書き換えても大丈夫なのでしょうか?また,その場合は0から∞で積分しなくてはいけないのでしょうか?個人的にガウス積分を使いたいので,-∞から∞で積分したいのですが…
教えてください.宜しくお願いします.
Re: 光子のエネルギー平均値の計算
えり さんのレス (2009/04/20(Mon) 00:09)
ありがとうございます.
ということは,規格化因子がもう少し簡単になるということですか!!
無限級数和になるのですね…
ところで 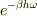 が1より小さいということは,もう自明なのでしょうか..
が1より小さいということは,もう自明なのでしょうか..
Re: 光子のエネルギー平均値の計算
mNeji さんのレス (2009/04/20(Mon) 00:58)
>ところで 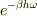 が1より小さいということは,もう自明なのでしょうか..
が1より小さいということは,もう自明なのでしょうか..
数学的に言えば自明でないと思います.でも,仮に1より大きいとすると,エネルギー準位が大きい程,存在確率が大きくなる事になり,物理的な観点から排除できると推測します.
ああ,熱力学的な問題には,大昔から悩まされました(笑).
#なお,エネルギ, 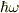 のhは「hbar」ですね.
のhは「hbar」ですね.
Re: 光子のエネルギー平均値の計算
mNeji さんのレス (2009/04/20(Mon) 09:07)
ちょっと茶々ですが... .
係数Aについて眺めていると,
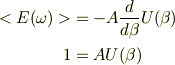
です.これからAを消去すると,
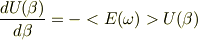
あたかも 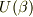 についての微分方程式と見えます.さらに
についての微分方程式と見えます.さらに 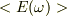 は平均値という意味では定数と考えると,変数分離形に見えます;
は平均値という意味では定数と考えると,変数分離形に見えます;
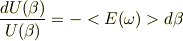
強引に積分すると,積分定数Cとして,
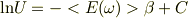
と,Uに付いての,微分と積分が出て来ます.
真偽の程は判りませんが....
Re: 光子のエネルギー平均値の計算
ASA さんのレス (2009/04/20(Mon) 17:49)
>平均値という意味では定数 これは幾らなんでも無茶苦茶ですな.
余談なら, 1光子あたりのエネルギーをεとすると <E>=<N>εであるから <N>=1/{exp(-βε)-1}と平均光子数はプランク分布になることが示せる. とか,分配関数Zとの関連を述べたほうが適切でしょう.
Re: 光子のエネルギー平均値の計算
mNeji さんのレス (2009/04/20(Mon) 20:06)
>これは幾らなんでも無茶苦茶ですな.
あはは,そうですね.変数分離形として積分するのは行き過ぎでした.風呂に入って閃いたと思って,寝ながら検算した筈なんですが.
その代り,
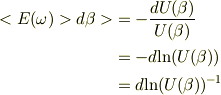
だから,
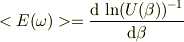
としておくと便利とか.以上で茶々モード終了します.
Re: 光子のエネルギー平均値の計算
ASA さんのレス (2009/04/20(Mon) 20:50)
一般に <E(T)>=-∂lnZ(T)/∂βですから, シングルモードアンサンブルとしての分配関数Zが,U(β)です.
Re: 光子のエネルギー平均値の計算
mNeji さんのレス (2009/04/21(Tue) 05:30)
えりさん,元のご質問に戻しますと,
>シグマをインテグラルで書き換えても大丈夫なのでしょうか?
については,これまでに述べて来た様に,光子のように元来が離散系の場合,積分に置き換えられないものだと思います.
ただし,一般的には,気体の熱平衡の論議では,運動エナジや回転エナジの場合は連続系になるので,いやでも積分になるのだと思います.
これ以上深い説明は,自分には出来ません.残念な事に,私は大昔,熱力学や熱統計学を捨てたからです.
ぜひとも,今回のご質問点を明確にされるように頑張って下さい.
Re: 光子のエネルギー平均値の計算
mNeji さんのレス (2009/04/21(Tue) 11:11)
さらに元々のお話;
>「角振動数ωの光子はエネルギー 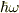 をもつ粒子として振舞う.n光子状態のエネルギーは
をもつ粒子として振舞う.n光子状態のエネルギーは 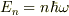 となる.
となる.
について,コメントをさせて戴きます.今回の問題は,黒体輻射の問題がベースだろうと察します.従って,周りが温度Tの熱浴の内部の光子系の熱平衡を考えるのだろうと思います.
したがって,この問題の前には,角振動数ωをもつ光子がもつ位相密度を出しているとおもわれます.今回のご質問は,その条件下で光子が熱浴とエナジを交換しながら,エナジ準位 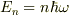 を上下して行く時に,それぞれの準位に在る存在確率が
を上下して行く時に,それぞれの準位に在る存在確率が 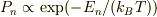 とした場合の計算と推測しました.
とした場合の計算と推測しました.
コメントの順番が混乱してしまって済みませんでした.
Re: 光子のエネルギー平均値の計算
えり さんのレス (2009/04/21(Tue) 12:34)
ASA様,mNeji様,どうもありがとうございました. シグマをインテグラルに書き換えられない理由はわかりました.確かに,光子は離散型で表されますものね…積分はできませんね..
また,
>数学的に言えば自明でないと思います.でも,仮に1より大きいとすると,エネルギー準位が大きい程,存在確率が大きくなる事になり,物理的な観点から排除できると推測します.
に関しても,物理的に考えるということが大切ですね;数学的に見ていました.
さらに
>今回の問題は,黒体輻射の問題がベースだろうと察します.従って,周りが温度Tの熱浴の内部の光子系の熱平衡を考えるのだろうと思います.
そんな問題が背景にあったのですね!?ここでは数学的な内容しか問われていないような気がするのですが,参考になりました.
これできれいな答えになりそうです.どうもありがとうございました.
Re: 光子のエネルギー平均値の計算
えり さんのレス (2009/04/22(Wed) 00:09)
すいません.後でよくよく問題を見てみたら,思いきり黒体輻射のことが書いてありました;やはり背景になっていたみたいです.
この記事を読んでから授業で詳しい説明を受けたので,一層理解が深まりました.どうもありがとうございました.
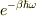 の無限級数和ですよね.
の無限級数和ですよね.