Poisson括弧

Poisson括弧

トビラ．． さんの書込 (2009/04/18(Sat) 22:00)

皆さんこにゃにゃちわ poissonの括弧を使った計算でわからないことがあるので，どうかよろしくお願いします． まず，Poisson括弧を

[A,B]=\int \left\{ \frac{\partial A}{\partial \lambda_i}\frac{\partial B}{\partial \pi^i}-\frac{\partial B}{\partial \lambda_i}\frac{\partial A}{\partial \pi^i}\right\}dx

と定義します．ここで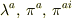， \lambda^a,\,\pi^a,\,\pi^{ai} は正準変数です．この２つの関係式は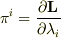， \pi^i=\displaystyle\frac{\partial \mathbf L}{\partial \lambda_i} とします．ここで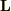， \mathbf L はLagrange関数です．ラテン字（例えば a などは）1〜３までを示すものとします．また，指標が上下に現れた時は１〜３まで合計を取るものとします．そうすると，本によると

\pi^{mn}[\pi^i,\, \nabla _m \lambda_n]=\nabla _m\pi^{mi}

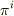ここで， \pi^i は密度量なので，右辺の共変微分は 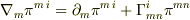\nabla_m \pi^{m\,i}=\partial _m \pi^{m\,i}+\Gamma^i_{mn}\pi^{mn} となっているのですが，左辺をいくら計算しても右辺のようにはなりません． 僕が計算すると，上述のようにはならず，

\pi^{mn}[\pi^i,\, \nabla_m \lambda_n]=\pi^{mn}[\pi^i,\,\partial _m\lambda_n -\Gamma^a_{mn}\lambda_a]=\pi^{mn}[\pi^i,\,\partial _m \lambda_n]-\Gamma ^a_{mn}[\pi^i,\, \lambda_a]
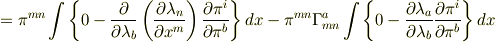
=\pi^{mn}\int \left\{ 0-\frac{\partial }{\partial \lambda_b}\left( \frac{\partial \lambda_n}{\partial x^m}\right)\frac{\partial \pi^i}{\partial \pi ^b}\right\} dx-\pi^{mn}\Gamma^a_{mn}\int \left\{0- \frac{\partial \lambda _a}{\partial \lambda _b}\frac{\partial \pi^i}{\partial \pi^b}\right\}dx
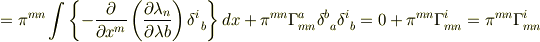
=\pi^{mn}\int\left\{ -\frac{\partial }{\partial x^m}\left( \frac{\partial \lambda_n}{\partial \lambda b}\right)\delta ^i_{\,\,\, b}\right\} dx+\pi^{mn}\Gamma^a_{mn}\delta ^b_{\,\,\, a}\delta ^i_{\,\,\, b}=0+\pi^{mn}\Gamma^i_{mn}=\pi^{mn}\Gamma^i_{mn}

となって計算が合わないんです．どうかほんの少しのヒントでいいので，どうかアドバイスお願いします． （説明不足でしたら，ご指摘ください．） へ・・・ヘルプ，ミ，ミィ〜〜〜

＊追記 ジョンさん？関係ない話ですが，ジョンさんはバイセコーギャックマンってひと知りませんか？昔，僕の親友でジョンって人いたんでつい・・・

Re: Poisson括弧

トビラ．． さんのレス (2009/04/19(Sun) 01:09)

すみません，解決しました．僕の単純な計算ミスでした． ご迷惑をおかけしました．