変分法

変分法

だそらん さんの書込 (2009/04/15(Wed) 16:14)

はじめまして，解析物理をやりたくてこちらのサイトで変分法の項を読ませていただきました． そこで，式変形がわからなくなったので質問させていただきます．

こちらのページの(5)式で，1行目から2行目への式変形ですが なぜこのような和の形になるのかがわかりません． ご教授願います．よろしくおねがします．

Re: 変分法

Yokkun さんのレス (2009/04/16(Thu) 13:31)

だそらんさん，こんにちは．

ちょっと私の手には余るかもしれませんが．

多変数関数 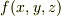f(x,y,z) が与えられ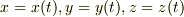， x=x(t),y=y(t),z=z(t) という関数関係があるとき，

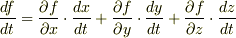
\frac{df}{dt}=\frac{\partial f}{\partial x}\cdot\frac{dx}{dt}+\frac{\partial f}{\partial y}\cdot\frac{dy}{dt}+\frac{\partial f}{\partial z}\cdot\frac{dz}{dt}

これがチェーンルールですね．すると，関数 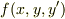f(x,y,y^\prime) の場合，

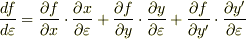
\frac{d f}{d \varepsilon}=\frac{\partial f}{\partial x}\cdot\frac{\partial x}{\partial \varepsilon}+\frac{\partial f}{\partial y}\cdot\frac{\partial y}{\partial \varepsilon}+\frac{\partial f}{\partial y^\prime}\cdot\frac{\partial y^\prime}{\partial \varepsilon}

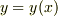となります．しかるに， x は y=y(x) の独立変数であり，関数形を変えるパラメータである \varepsilon に対して関数関係をもっていません．したがって，上の第1項はゼロになるわけでしょう．そしてまた， \varepsilon による微分と x による積分は順序を入れ替えてよいということになると思います．

Re: 変分法

だそらん さんのレス (2009/04/17(Fri) 22:41)

レスありがとうございます． どうやらチェーンルールをちゃんと理解していなかったようです． 説明を見てわかりましたが，念のために偏微分を見直してきます． ありがとうございました．