ガンマ関数からスターリングの公式
ガンマ関数からスターリングの公式
えり さんの書込 (2009/04/15(Wed) 15:19)
ご無沙汰しております. ガンマ関数からスターリングの公式を導く問題(ですが本題に行く前につまづいています)なのですが,変数変換がうまくいきません.
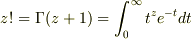 の右辺の積分で,
の右辺の積分で,
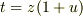 とおくと,
とおくと,
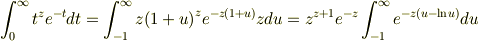
となってしまいました.本当は右辺が,変数変換をすると
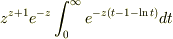 となるようなのですが,こうなりません.そもそも積分範囲も違うし,eの肩の上もぴったり合いません.
何故でしょうか..やはりuの置き方が悪かったのでしょうか,それとももう一段階踏むのでしょうか.教えてください.よろしくお願いします.
となるようなのですが,こうなりません.そもそも積分範囲も違うし,eの肩の上もぴったり合いません.
何故でしょうか..やはりuの置き方が悪かったのでしょうか,それとももう一段階踏むのでしょうか.教えてください.よろしくお願いします.
Re: ガンマ関数からスターリングの公式
えり さんのレス (2009/04/16(Thu) 15:34)
掲示板はどちらかというと数学寄りの方がいいのでしょうか? 科目は統計力学(まだ準備段階ですが…)なのですが(汗)
Re: ガンマ関数からスターリングの公式
toorisugari no Hiro さんのレス (2009/04/16(Thu) 18:29)
ここでかまわないですが,簡単に答えられそうには見えません. 問題および答えを正確に記述してくれますか?
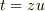 と置くと
と置くと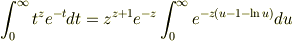
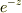 を出すために
を出すために 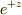 を足すということに頭が回りませんでした…
どうもありがとうございました.
を足すということに頭が回りませんでした…
どうもありがとうございました.