初歩にもどります．．．

初歩にもどります．．．

数学迷い人↓ さんの書込 (2009/04/14(Tue) 01:04)

根本的な理解が足りないこと，実感しました． 一歩ずつ確かめていきます．

まずは，ベクトル解析なんですが，

ベクトル場A（x,y,z）, スカラー場f（x,y,z）の時， ?ｆA ?∇ｆ ?∇・A の計算はどのように行っていきますか？

自分の計算での答え ?（x^2,y^2,z^2） ?（1,1,1） ?３

Re: 初歩にもどります．．．

mNeji さんのレス (2009/04/14(Tue) 02:02)

＞根本的な理解が足りないこと，実感しました． ＞一歩ずつ確かめていきます．

とても素晴らしいアイデアだと思います．じっくりと進めて下さいね．

ベクトル場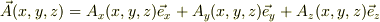： \vec A(x,y,z) = A_x(x,y,z)\vec e_x +A_y(x,y,z)\vec e_y +A_z(x,y,z)\vec e_z スカラー場f（x,y,z） の時，

? fA ：結果はベクトル

f(x,y,z)\vec A(x,y,z) &= f(x,y,z)[A_x(x,y,z)\vec e_x +A_y(x,y,z)\vec e_y +A_z(x,y,z)\vec e_z]\\&= f(x,y,z)A_x(x,y,z)\vec e_x +f(x,y,z)A_y(x,y,z)\vec e_y +f(x,y,z)A_z(x,y,z)\vec e_z

? ∇ｆ：結果はベクトル

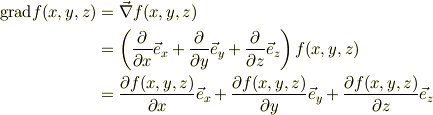
\mathrm{grad }f(x,y,z) &= \vec \nabla f(x,y,z)\\&= \left( \frac{\partial }{\partial x}\vec e_x +\frac{\partial }{\partial y}\vec e_y +\frac{\partial }{\partial z}\vec e_z \right) f(x,y,z)\\&= \frac{\partial f(x,y,z)}{\partial x}\vec e_x +\frac{\partial f(x,y,z)}{\partial y}\vec e_y +\frac{\partial f(x,y,z)}{\partial z}\vec e_z

? ∇・A：結果はスカラ

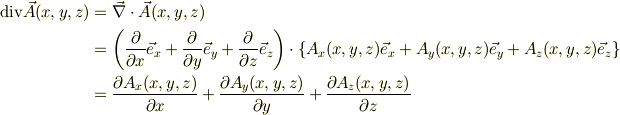
\mathrm{div} \vec A(x,y,z) &= \vec \nabla \cdot \vec A(x,y,z)\\&= \left( \frac{\partial }{\partial x}\vec e_x +\frac{\partial }{\partial y}\vec e_y +\frac{\partial }{\partial z}\vec e_z \right) \cdot \{ A_x(x,y,z)\vec e_x +A_y(x,y,z)\vec e_y +A_z(x,y,z)\vec e_z\}\\&= \frac{\partial A_x (x,y,z)}{\partial x} +\frac{\partial A_y (x,y,z)}{\partial y} +\frac{\partial A_z (x,y,z)}{\partial z}

具体例は，ベクトルやスカラ関数を具体的に示して戴いてからにします．

Re: 初歩にもどります．．．

ジョン さんのレス (2009/04/14(Tue) 09:59)

一つ一つ丁寧に見ていくとわかりました．

gradのベクトルを成分表示から，数式にしていますが，

（δ/δx , δ/δy , δ/δz ) ↓ （δex/δx＋δey/δy＋δez/δz )

この変換は，それぞれの単位ベクトル（基本ベクトル）を使ってるからいいんですよね？

Re: 初歩にもどります．．．

ジョン さんのレス (2009/04/14(Tue) 10:01)

てか，横からすいません．

私もベクトル解析が苦手なんで，一緒に参加させてください．

Re: 初歩にもどります．．．

mNeji さんのレス (2009/04/14(Tue) 11:05)

＞gradのベクトルを成分表示から，数式にしていますが，

私は成分だけを行ベクトルや列ベクトルで表示するのは好きではありませんが；

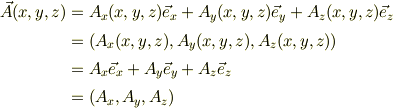
\vec A(x,y,z) &= A_x(x,y,z)\vec e_x +A_y(x,y,z)\vec e_y +A_z(x,y,z)\vec e_z\\&= (A_x(x,y,z), A_y(x,y,z), A_z(x,y,z))\\&= A_x\vec e_x +A_y \vec e_y +A_z \vec e_z\\&= (A_x, A_y, A_z)

注意する点は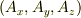， (A_x, A_y, A_z) は三つのスカラ関数が並んで1行*3列の行列を示しているのであって，三つのスカラ関数の和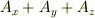， A_x +A_y +A_z では無いことです．

スカラ関数の勾配(grad)は，その名称から判る様に，スカラ関数の変化の方向と強さを示すものです．偏微分演算子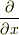， \frac{\partial}{\partial x} などを成分とするヴェクトル型の演算子，ナブラ(nabla)；

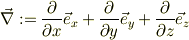
\vec \nabla := \frac{\partial }{\partial x}\vec e_x +\frac{\partial }{\partial y}\vec e_y +\frac{\partial }{\partial z}\vec e_z

をスカラ関数f(x,y,z)に作用させると，f(x,y,z)の勾配(grad)が出来ると考えます．これをベクトル場と同様に，1行3列の表現にすれば，

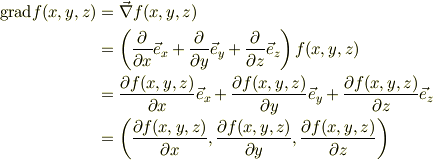
\mathrm{grad }f(x,y,z) &= \vec \nabla f(x,y,z)\\ &= \left( \frac{\partial }{\partial x}\vec e_x +\frac{\partial }{\partial y}\vec e_y +\frac{\partial }{\partial z}\vec e_z \right) f(x,y,z)\\ &= \frac{\partial f(x,y,z)}{\partial x}\vec e_x +\frac{\partial f(x,y,z)}{\partial y}\vec e_y +\frac{\partial f(x,y,z)}{\partial z}\vec e_z\\&= \left(\frac{\partial f(x,y,z)}{\partial x}, \frac{\partial f(x,y,z)}{\partial y}, \frac{\partial f(x,y,z)}{\partial z} \right)

となります．

＃私は，通常のユークリッド空間に出て来るベクトルAを表示する為に，ボールド体をつかうより，Aの上に「→」を付けるのが好きです． ＃ですから，ナブラ演算子も逆三角形(このギリシャ語がナブラだったと思いますが)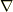，「 \nabla 」だけにしないで「 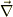\vec \nabla 」としています．