きつね さんの書込 (2009/04/14(Tue) 00:48)

かなり本を読んだのですがダメでした

ローレンツ変換の途中でなんで x'=A(x-vt) とするのか教えてください． なぜAはxだけではなくvtにもかかるのでしょうか？ そもそもxとはどこからどこまでの距離で，x'はどこからどこまでの距離なのですか？ x'=x-vtじゃダメなのですか？

Yokkun さんのレス (2009/04/19(Sun) 11:33)

何度か質問を読みましたが，回答しにくい事この上ないですね． なぜだか考えてみました．

(1)ローレンツ変換を導出する途中でなぜ 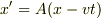とおけるのか．

これは，座標変換の本質にせまるかなり高度な問題なのですね．一方，

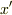(2)そもそも とはどこからどこまでの距離で， はどこからどこまでの距離なのか．

これは，最も基本的な座標の意味を問われているのです． まずは，２つの系の座標の意味をよく理解することが先決と思われます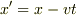． すなわちガリレイ変換じゃダメだというのでローレンツ変換がそれに代わるわけです．(2)の問いが解決されていないと，ガリレイ変換の意味さえ理解されていないと判断せざるを得ません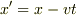． の意味をどう理解されていますか？

Yokkun さんのレス (2009/04/19(Sun) 14:25)

(2)について解決されているものとして，(1)について考えます．一般には次のように導出されています．

まず， 軸方向への相対速度 をもつ２つの系 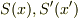の間の座標変換を考えるのですから，空間の等方性から変換に 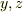は入り込まないだろうという推論が成り立ちます．したがって，変換を 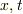の1次変換であるものと仮定します（これは数学的には証明がされているそうですが，この部分が「高度な問題」といった意味です）．すると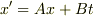， とおけます．ここで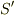， 系の原点に静止した時計の 系に対する運動は 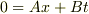と書けるはずですから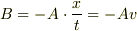， と係数 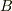が定まる，という具合に説明されています．

きつね さんのレス (2009/04/20(Mon) 20:25)

ありがとうございます．

いろいろと本を読みまくって，わからなくてイライラ混じりで書き込んでいました．ゴメンなさい． 本によってはtが時間のように記載されていたり，別の本によっては時刻のように記載されていたりで，実際はどれが正しいのかわからなかったので，アインシュタインの書いた本を見たら一瞬にして求められていたので，わからずにイライラしていました．

xが一秒で光が到達する距離であるとすると，x'もS'系で１秒で光が到達する距離と思っています． また，tおよびt'も時間であって，時刻ではないと思っているのですが，あっていますか？

Yokkun さんのレス (2009/04/20(Mon) 21:56)

>xが一秒で光が到達する距離であるとすると，x'もS'系で１秒で光が到達する距離と思っています．

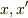は，距離ではありません．物体の運動を記述する座標を示しています．つまり， 系で時刻 に観察したある物体の位置が， で表された場合（すなわち原点からの距離が 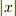で，また の符号で方向が表される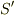）， 系で観察される同じ物体の位置と時刻 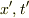が 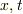とどういう関係を持つか，というのがローレンツ変換の意味です．

>また，tおよびt'も時間であって，時刻ではないと思っているのですが，あっていますか？

通常，単に 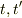と書かれるとき，これらは時間ではなく時刻を表しています．したがって，時間原点が指定されなければなりません．多くのテキストの初歩的な説明では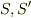， 系の原点が一致した瞬間を 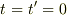としているのではないですか？

位置も時刻も原点の選択は自由なので，それぞれの変化分をとって 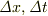や 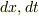などとして変換を表現する場合もありますが，その場合は変位（方向つきの距離）および時間変化を指すことになります．

きつね さんのレス (2009/04/22(Wed) 20:57)

ありがとうございます． 根本的に間違っていたのですね． ようやく頭の中が整理できました．

もう一つ聞いていいですか？ S系から見るとS'系は動いていると思うのですが，S'系から見るとS系が動いていることになるので， お互いがお互いの時計が遅れていると感じると思います． もし，同じ点から別方向に動いて，両者とも同じようにUターンして戻ってきて両者の時計を見た場合， 別方向に動いているときはお互いの時計が遅れているように見えて，Uターン後にスタート地点に戻ってきて時計を照らし合わせると同じ時刻になっていると思うのですが， 遅れていた時計がいつ戻ったのでしょうか．

Yokkun さんのレス (2009/04/22(Wed) 21:31)

>遅れていた時計がいつ戻ったのでしょうか．

双子のパラドックスの発展形ですね．両者がまったく対等の運動をしているという点で通常の問題場面と異なります．対称性から明らかなように，両者が再び出会ったとき，両者の時計は同時刻をさしているはずですね．

この問題を疑問の余地なく説明するには，一般相対性理論に踏み込む必要があると思われます．実は，両者の時計が一致して観測されるのは，Uターンの途中で一瞬相対速度がゼロになったときにも起こります．同様に，帰ってくる間相互に「あちらの時計はおくれている」と観測していたのに，急ブレーキをかけて静止した直後から同時刻をさして見えるわけですね．

当然急ブレーキをかけているその間に秘密があります．急ブレーキをかけられた系は加速系になり，慣性系ではありませんから厳密には特殊相対性理論の範囲では議論できないのです．加速系では慣性力が重力と同等の役割を持ち，その慣性力＝重力の存在によって慣性系に対する「正味の」時間のおくれが生じると解釈されます．出発点および到着点を慣性系であるものとして，もしそこに固定された時計があれば，両者の時計とも固定された時計に対しておくれているはずです．これが，本来の双子のパラドックスですね．

きつね さんのレス (2009/04/23(Thu) 22:01)

一般相対性理論は見てみましたが，まるで手が出ません． そのうち，理解したらチャレンジしてみます．

なかなか難しい分野ですね

特殊のほうはだいぶ理解できてきました． ありがとうございました