初めまして

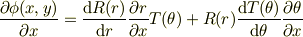
$\frac{\partial \phi(x,y)}{\partial x} = \frac{\mathrm{d} R(r)}{\mathrm{d}r}\frac{\partial r}{\partial x}T(\theta) +R(r)\frac{\mathrm{d} T(\theta)}{\mathrm{d}\theta}\frac{\partial \theta}{\partial x}$

最後の部分に付いては,さらに

を使えますね．同様に，yについての偏微分も求まります．

同様に，２階の偏微分も計算出来る筈ですね，フ〜．

Re: 初めまして

ジョンさんのレス (2009/04/13(Mon) 21:47)

ありがとうございます．

う〜ん・・・，微分記号にモヤが・・・．微分記号dとありますが，偏微分記号のδとは意味が違ってくるのでしょうか？

そして，偏微分の結果が，どのようにしたら，ベッセルの微分方程式x^2y''+xy'+(x^2-n^2)y=0となっていくのでしょうか？

Re: 初めまして

ジョンさんのレス (2009/04/13(Mon) 21:53)

ちなみに，δθ/δx＝−y(cosθ)^2/x^2 で合っていますか？お手数ですがお願いします．

Re: 初めまして

mNeji さんのレス (2009/04/13(Mon) 23:31)

＞微分記号dとありますが，偏微分記号のδとは意味が違ってくるのでしょうか？

物理では，ある独立変数xの関数f(x)の(常)微分は

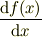
$\frac{\mathrm{d} f(x)}{\mathrm{d} x}$

と書く事が多いです．この場合，dは変数でなくて，微分操作をするシンボルという感触だろうと思います．でも，数学系の方々は，通常の「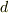」を用いる様です．

他方，数学・物理で共通して，偏微分記号としては，「∂」が使われています．

「δ」は，関数f(x)に，微小の関数を付ける様な場合；

・関数f(x)の変分＝δf(x)

といった使い方があると思いますが，それほど厳密な定義はないと思います．

＞そして，偏微分の結果が，どのようにしたら，＞ベッセルの微分方程式x^2y''+xy'+(x^2-n^2)y=0となっていくのでしょうか？

先に書いた様に，xの偏微分について考えると；

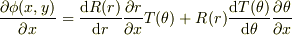
ですが，両辺をφ(x,y)＝R(r)T(θ)で割ると，右辺は「rだけの関数」と「θだけの関数」の和に成る事が判ります．ですからヘルムホルツ方程式もどうような二つの微分方程式の和になります．従って，それぞれの微分方程式が常数となることがわかります．ここら辺の事情は特殊関数の解説書などをご覧下さい．

＞ちなみに，δθ/δx＝−y(cosθ)^2/x^2 で合っていますか？

$\frac{\partial \theta}{\partial x} &= \frac{\mathrm{d} \theta}{\mathrm{d}\tan(\theta)}\frac{\partial \tan(\theta)}{\partial x}\\ &=1/\left[\frac{\mathrm{d}\tan(\theta)}{\mathrm{d} \theta}\right]\cdot \frac{\partial \tan(\theta)}{\partial x} \\&= \{\cos(\theta)\}^2 \cdot y(-x^{-2})\\&= -\frac{x^2}{r^2} \frac{y}{x^2}\\&= -\frac{\sin(\theta)}{r}$

で良いみたいですね．

Re: 初めまして

ジョンさんのレス (2009/04/14(Tue) 00:45)

ご丁寧にありがとうございます．

たしかに，右辺は，rだけの関数＋θだけの関数にできました．しかし，この式から，まだベッセルの微分方程式への持っていき方がわかりません．このサイトの変数分離を参考にしたのですが，両辺にdxをかけて積分をしています．しかし，この場合では，この式にdxをかけてしまうと，今までの秩序を崩してしまうのではないでしょうか？長々とわかりにくいかもしれないですが，とりあえず，前に進みたいので，この後の過程を教えてください．お願いします．

Re: 初めまして

ジョンさんのレス (2009/04/14(Tue) 00:49)

さらに追加ですいません． xでの偏微分とyでの偏微分を統合するときは，単にそれぞれを足し合わせれば良いのでしょうか？

Re: 初めまして

mNeji さんのレス (2009/04/14(Tue) 01:41)

＞しかし，この式から，まだベッセルの微分方程式への持っていき方がわかりません．

ここから先は細々したことが多いので書き難いのですし，今手元にこの手の解説書をもっていないので説明しようとすると時間が掛かります．

大雑把に言えば，角度の成分の微分方程式の固有値問題を解く事が先で，その次に度半径成分の微分方程式としてベッセルの微分方程式が出て来ると思いました．

従って，ラプラシアンの極座標表現，微分方程式などの参考書をご覧になって，大筋の流れをご理解させることをお勧めします．インターネットでも解説はあるとおもいます．

＞xでの偏微分とyでの偏微分を統合するときは，単にそれぞれを足し合わせれば良いのでしょうか？

はい，それで良いと思います．

[home] [掲示板] [ページの先頭]