機械力学 バネ滑車
機械力学 バネ滑車
ひろ さんの書込 (2009/04/13(Mon) 05:18)
はじめまして.初投稿させてもらいます. 私は現在工学部の学部4年生です.院試の過去問を解いていたときにわからない分からない問題があったので質問させてもらいます.
〜問題文〜 中心軸Oのまわりに自由に回転する質量M,半径aの円板に糸をかけて,一方は地面に固定され,一方は質量がmのおもりが吊り下げられている.円板の中心Oは天井からヤング率kのバネで吊り下げられている.糸の質量は無視でき,糸は伸びず,すべらないとする. いま,おもりの垂直方向の変位がx(t),円板の垂直方向の変位がy(t),中心からの回転角がθ(t)で表されるものとする.変位,速度,加速度は下方に向かって正とする.横方向への移動はないものとする. ばねに力が加わらない初期長さl0のときを,初期位置x(0)=0,y(0)=0,θ(0)=0とする.
問2x(t)とy(t)の関係,x(t)とθ(t)の関係を求めよ.変位は微小であるとして,sin(a)=a,tan(a)=a and cos(a)=1とみなして良い.
この問なんですが,私が考えた式が次のようになりました. x(t)=y(t)+a*sin(θ(t)) →x(t)=y(t)+a*θ(t) おもりの変位xは,バネによる変位yと円板の回転によってできる変位θを足し合わせればよいと思いました. しかしこれでは,xとyとθの関係式になってしまいます. xとy,xとθの関係式はどのように作ればよいのでしょうか? よろしければご教授願います.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/13(Mon) 10:26)
ひろさん,初めまして.
逆に質問なのですが, >円板の垂直方向の変位がy(t)
というのが理解出来ません.天井から円盤をバネで吊っているので,円盤の中心位置中心軸Oとバネの伸びは一致するように感じます.
ヒョットして, >質量がmのおもりが吊り下げられている.
この,おもりの変位ではありませんか?
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/13(Mon) 12:09)
mNejiさん,さっそくの返答ありがとうございます. ここに図が出せないので,説明不足になってしまい申しわけありませんでした. y(t)は円板の中心から下方に矢印が引いてあるのでy(t)はバネの伸びになると思います. また,質量がmのおもりのほうの変位には別にx(t)というのがおかれています. mNejiさんの質問の意図と違う返答をしていた場合,申し訳ありません.
雑で申し訳ありませんが図を描きました.
よろしかったら参考にしてください.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/13(Mon) 13:07)
図を拝見しました.私の読解が間違った様ですね.
始めに静止の位置にあったところから,点Oがy(t)だけさがっとします.その時に,右の糸はaθ(t)まかれ左の糸はaθ(t)だけ出て行きます.錘の変化は,点Oの落下分と左の糸の繰り出しの和ですから,
x(t) = y(t) + aθ(t)
となります.「糸と円盤が滑らない」と仮定すれば,
y(t) = aθ(t)
となります.恐らく出題のなかに書いてありませんか?
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/13(Mon) 13:27)
mNejiさん,返答ありがとうございます. y(t)=aθ(t)ならば,xとyの関係式がx(t)=2y(t), xとθの関係式がx(t)=2aθ(t) ということになるんですね.
問題文は最初に書いたものがすべてです. 大変わかりやすく教えていただきありがとうございました.
この問題の続きでわからない問いはここの続きで質問してもよろしいのでしょうか?
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/13(Mon) 13:36)
>この問題の続きでわからない問いはここの続きで質問してもよろしいのでしょうか?
もちろんOKだと思います.でも,私のようにオッチョコチョイもいるので,ご注意下さいね.
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/13(Mon) 14:32)
他の問いも自分なりに解いてみましたが,答えがないので考え方と答えがこれでいいのか教えていただけると幸いです.
問1O点まわりの円板の慣性モーメントを求めよ.
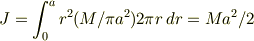
この問いは教科書から理解できました.
問3バネのポテンシャルエネルギーVs,円板のポテンシャルエネルギーVc,おもりのポテンシャルエネルギーVwをそれぞれ求めて,ポテンシャルエネルギーの和Vをy(t)の関係式で表せ.
Vs=-ky(t)^2/2 ←バネの位置エネルギーの式よりこのようになりました. Vc=Mgy(t)←物体の位置エネルギーの式よりこのようになりました. Vw=mgx(t)⇒Vw=2mgy(t)←物体の位置エネルギーの式と問2よりこのようになりました. よって,V=-ky(t)^2/2 + Mgy(t) + 2mgy(t)
問4A点回りの円板の慣性モーメントJAを求めよ. 先ほどあげた図にA点を書いてませんでした.Aは右の糸と円板の接地点がA点です.(円板中心から真右に行った点) JA=J+Ma^2=3Ma^2/2 この問いも教科書により理解しました.
問5円板の運動エネルギーをTc,おもりの運動エネルギーをTwとして運動エネルギーの和Tを求めよ.
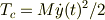
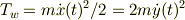
よって, 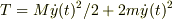 という風に考えました.
現在ここまで,解き終わりました.
もし,間違っている箇所があった場合,指摘願います.
という風に考えました.
現在ここまで,解き終わりました.
もし,間違っている箇所があった場合,指摘願います.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/13(Mon) 15:21)
ざっと拝見した所では; >円板の運動エネルギーをTc
では,重心の並進運動エネルギに重心廻りの回転エネルギを加える必要があるようにおもいます.
Re: 機械力学 バネ滑車
Yokkun さんのレス (2009/04/13(Mon) 16:01)
ひろさん,mNejiさん,こんにちは.
横から失礼します.あれよという間にだいぶ進まれましたね. ポテンシャルエネルギーの符号がすべて逆のように思われます.
ちなみに,
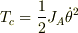 となるところがミソですね.A点は瞬間の回転中心になるために,そのまわりの慣性モーメントで計算した回転のエネルギーは,円板の運動エネルギーのすべてになるわけです.
となるところがミソですね.A点は瞬間の回転中心になるために,そのまわりの慣性モーメントで計算した回転のエネルギーは,円板の運動エネルギーのすべてになるわけです.
あと一点気になったことですが,
>x(t)=y(t)+a*sin(θ(t))
→x(t)=y(t)+a*θ(t)
と書かれていますが,これははじめから 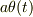 であって,
であって, 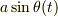 として近似しているかのような考えはそもそも間違っていますから,気をつけてください.
として近似しているかのような考えはそもそも間違っていますから,気をつけてください.
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/13(Mon) 16:32)
Yokkunさん,返信ありがとうございます. 自分の学習不足で申し訳ありませんが,ポテンシャルエネルギーの符号が逆になるというところを少し詳しく教えていただけないでしょうか?
運動エネルギーのほうは
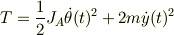
というようになるのでしょうか?
最後の 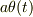 の箇所は以後気をつけたいと思います.
細部の指摘ありがとうございます.
の箇所は以後気をつけたいと思います.
細部の指摘ありがとうございます.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/13(Mon) 17:51)
Yokkunさん,
>ちなみに,
> 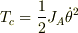 >となるところがミソですね.
>となるところがミソですね.
とすると,「並進運動しながらも回転している系」と「静止しているが回転している系」の運動エネルギは同一ということでしょうか?
また, >ポテンシャルエネルギーの符号がすべて逆のように思われます.
とありますが,題意により座標は下向きの方向を正に取っているので,重力ポテンシャルに関しては,符号は正でいいのではありませんか?
Re: 機械力学 バネ滑車
Yokkun さんのレス (2009/04/13(Mon) 18:25)
ひろさん,運動エネルギーは初めのままでいいですよ.問4が先行している意味を尊重すれば,J_Aを使うことも出来ますねということです.
>「並進運動しながらも回転している系」と「静止しているが回転している系」の運動エネルギは同一ということでしょうか?
瞬間の回転中心がわかれば,そのまわりの回転が注目している物体の運動のすべてであるということです.
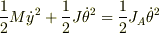 がそれを示していますね.
がそれを示していますね.
>題意により座標は下向きの方向を正に取っているので,重力ポテンシャルに関しては,符号は正でいいのではありませんか?
下向きを正にとっているから,符号は負になるわけです.重力による位置エネルギーは高い所ほど大きいわけですから.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/13(Mon) 18:49)
>瞬間の回転中心がわかれば,そのまわりの回転が注目している物体の運動のすべてであるということです.
> 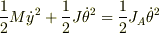 >がそれを示していますね.
>がそれを示していますね.
そうですか,知りませんでした.私は,頭が固いので,重心運動とそれに付いての回転運動と分けて考えているほうが確実に思えます.恐らく,出題者の方は,J_Aについて出題をしているので,「瞬間の回転中心」を想定しているのでしょうね.
>重力による位置エネルギーは高い所ほど大きいわけですから.
あ,そうですね,二重に間違えています.私の意見は撤回します.
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/13(Mon) 19:04)
mNejiさん,Yokkunさん返答ありがとうございます. 位置エネルギーのところは理解することが出来ました. ありがとうございます. ということは,位置エネルギーは
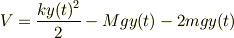
というふうになるんですね. ばねの位置エネルギーは高さではなくて伸びなので正という考えでいいのでしょうか?
Re: 機械力学 バネ滑車
Yokkun さんのレス (2009/04/13(Mon) 19:20)
>ばねの位置エネルギーは高さではなくて伸びなので正という考えでいいのでしょうか?
伸びても縮んでも正なのですね.yの正負に関係なく正なのです.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/13(Mon) 19:30)
「瞬間の回転中心」というのは面白い考え方だとおもいますが,この点は,静止系(この場合,天井)から見て静止している必要は在るのでしょうかね?
Re: 機械力学 バネ滑車
Yokkun さんのレス (2009/04/13(Mon) 19:32)
>静止系(この場合,天井)から見て静止している必要は在るのでしょうかね?
もちろんです.静止系に対して静止していなければ瞬間の回転中心という概念自体の意味がなくなります.
逆でした.動いてなければ瞬間の回転中心という概念自体の意味がなくなります.
自分で書いていて笑ってしまいます.両方正しいのですよね.幾何学的には静止しているから瞬間の「回転中心」であり,物理的には動いていく点であるからまた,「瞬間」の回転中心であるわけだと思います.
ぐちゃぐちゃですね.トホホ.物理的には瞬間的に速度がゼロ.幾何学的に動いていく?
ちなみに瞬間中心から見ると, 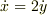 がはっきり見えますね.
がはっきり見えますね.
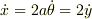
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/13(Mon) 20:53)
>物理的には瞬間的に速度がゼロ.幾何学的に動いていく?
「点A」では,地面から引っ張られている糸に静止しているわけで「瞬間的に速度がゼロ」であるが,回転によってずれて行くわけですか.
そう考えると,自動車のタイアが地面とずれ無しに回転する場合も,ヨーヨーが天井に糸を固定して落下される場合も,そして以前,カマボコ状の回転を論議された場合も,みんな一緒ですね.
>ちなみに瞬間中心から見ると, 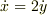 がはっきり見えますね.
がはっきり見えますね.
御意.グラフィックで速度分布の図示をすると面白そうですね.どっかに落ちてそう.
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/14(Tue) 01:13)
mNejiさん,Yokkunさん返答ありがとうございます. 返信が遅れてしまい大変申し訳ありません.
詳しい説明ありがとうございます. 続きの問も解いてみたので見ていただけると幸いです.
問6LAGRANGE関数を用いて,y(t)に関する微分方程式を求めよ.
L=T-Vラグランジュアン
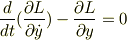
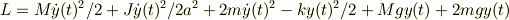
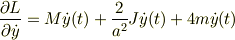
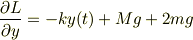
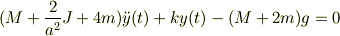
よって,
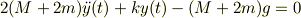
問7y(0)=0,y'(0)=0,M=2mの時の運動方程式を解け. M=2mなので,
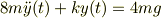
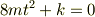
![t^2 + (\sqrt[]{\frac{k}{8m}})^2 = 0](http://hooktail.maxwell.jp/bbslog/572d6463d9c6b64586da4f91616dd37e.png)
よって,
![y(t)_A = C_1 cos{\sqrt[]{\frac{k}{8m}}t} + C_2 sin{\sqrt[]{\frac{k}{8m}}t}](http://hooktail.maxwell.jp/bbslog/ee5ad7a322ff8328fe89a09d8fd5c9eb.png)
ここでC1,C2は任意定数とする. 次に,未定係数法により,y(t) = aとすると,
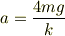
よって,
![y(t) = C_1 cos{\sqrt[]{\frac{k}{8m}}t} + C_2 sin{\sqrt[]{\frac{k}{8m}}t} + \frac{4mg}{k}](http://hooktail.maxwell.jp/bbslog/827d89b12acea65fc44d6c662450d61b.png)
![y'(t) = -\sqrt[]{\frac{k}{8m}}C_1 sin{\sqrt[]{\frac{k}{8m}}t} + \sqrt[]{\frac{k}{8m}}C_2 cos{\sqrt[]{\frac{k}{8m}}t}](http://hooktail.maxwell.jp/bbslog/87efca8fc7a1431308b96d8e11cac2c6.png)
ここで,y(0)=0,y'(0)=0より,
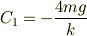
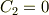
よって,求める運動方程式は,
![y(t) = -\frac{4mg}{k} cos{\sqrt[]{\frac{k}{8m}}t} + \frac{4mg}{k}](http://hooktail.maxwell.jp/bbslog/2270e89e18187104cc0e705900985639.png)
というようになりました.かなり,自信がない答えになりました. よろしければ,見ていただけないでしょうか.よろしくお願いします.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/14(Tue) 02:40)
途中の検算はしていませんが;
>問7y(0)=0,y'(0)=0,M=2mの時の運動方程式を解け.
>M=2mなので,
> 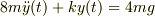 >
> 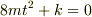
最後の式がどのように出たのかが判りかねます.単純に 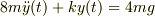 を整理して;
を整理して;
![8m\ddot y(t) &= -ky(t) +4mg\\&= -k[y(t) -4mg/k]](http://hooktail.maxwell.jp/bbslog/8bf8577fabddf7219215d02e5168e10f.png)
そこで変数をずらして, 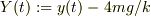 とすると重力項は消えるので線形微分方程式になり,簡単に解ける.
とすると重力項は消えるので線形微分方程式になり,簡単に解ける. 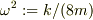 を導入して
を導入して
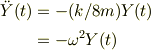
一般解は
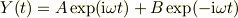
ですよね.y(t)に戻して,初期条件から積分定数A,Bは求まりますね.
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/14(Tue) 03:34)
mNejiさん,夜分遅くまでありがとうございます.
説明不足で申し訳ありませんでした.
最後の式 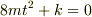 は,L(y)=R(x)の微分方程式は,
L(y)=R(x)の特殊解と,L(y)=0の一般解の足し合わせなので,
L(y)=0の特性方程式をtで表しました.
は,L(y)=R(x)の微分方程式は,
L(y)=R(x)の特殊解と,L(y)=0の一般解の足し合わせなので,
L(y)=0の特性方程式をtで表しました.
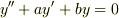 の一般解は,
の一般解は,
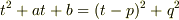 ⇒
⇒ 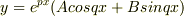 というものを使用して解きました.
というものを使用して解きました.
教えていただいた方法で解いてみました.
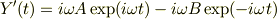
よって,
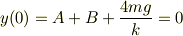
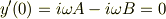
この連立方程式を解くと
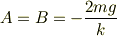
よって,AとBを代入して
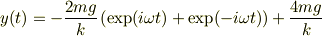
ここで,オイラーの公式を当てはめると
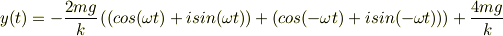
よって,
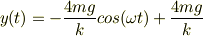
となり,自分で解いたものと一緒になりました. 教えていただいたほうが計算が少なくてわかりやすかったです. 大変わかりやすく,詳細に説明していただきありがとうございます.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/14(Tue) 08:48)
>最後の式 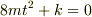 は,L(y)=R(x)の微分方程式は,
>L(y)=R(x)の特殊解と,L(y)=0の一般解の足し合わせなので,
>L(y)=0の特性方程式をtで表しました.
は,L(y)=R(x)の微分方程式は,
>L(y)=R(x)の特殊解と,L(y)=0の一般解の足し合わせなので,
>L(y)=0の特性方程式をtで表しました.
私も,書き終わった瞬間に,もしやと思いました(笑).
今の問題では,時間,tの微分方程式を扱っているので,特解を 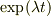 と仮定すると,その係数
と仮定すると,その係数  の特性方程式は...とする方が紛れないと感じます.
の特性方程式は...とする方が紛れないと感じます.
また,ラグランジェ方式の解法は好みでないので検算していませんので悪しからず.もしやるとすると,力とトルクを与えて運動量と角運動量の式から解きますかね.
いずれにしろ,Yokkunさんがご指摘された「瞬間的に速度がゼロ点」を明確に理解出来てとても嬉しいです.どうも有り難うございました.
Re: 機械力学 バネ滑車
Yokkun さんのレス (2009/04/14(Tue) 10:07)
夜を徹しての奮闘ごくろうさまでした.
>ラグランジェ方式の解法は好みでないので検算していませんので悪しからず.
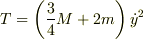 になりませんか?ラグランジアンの微分のところでJの項の係数を間違われたのではないでしょうか?
になりませんか?ラグランジアンの微分のところでJの項の係数を間違われたのではないでしょうか?
>もしやるとすると,力とトルクを与えて運動量と角運動量の式から解きますかね.
束縛力を初めから考慮する必要がないところが,ラグランジアンの強みですね.一度味をしめるとやみつきになります.でも,力とトルクから運動方程式をたてることはとても意味のあることだと思います.
Re: 機械力学 バネ滑車
Yokkun さんのレス (2009/04/14(Tue) 13:10)
よかった.今,再度指摘しようとしたところでした.^^;
剛体の回転運動を含む系において,重力に抗する慣性(重力による位置エネルギーの係数)と運動に関する慣性(運動エネルギーの係数)が一致することはまずないのです.こうした一般的な性質を理解していると,ミスに気づくのがはやくなります.
Re: 機械力学 バネ滑車
Yokkun さんのレス (2009/04/14(Tue) 13:45)
ごくろうさまでした.たぶん合っていると思います.
蛇足になりますが,系の力学的エネルギーは
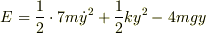 となりますが,定数の差は許されるので
となりますが,定数の差は許されるので
![E^\prime = \frac{1}{2}\cdot7m\left[\frac{d}{dt}\left(y-\frac{4mg}{k}\right)\right]^2+\frac{1}{2}k\left(y-\frac{4mg}{k}\right)^2=\frac{1}{2}\mu\dot{Y}^2+\frac{1}{2}kY^2](http://hooktail.maxwell.jp/bbslog/1b1c1357c2551ebe024275ccf94e6b13.png) と書けます.
すると,単振動のエネルギーの一般的な形式に一致するので,ただちに解が与えられたような形になることがわかりますね.
と書けます.
すると,単振動のエネルギーの一般的な形式に一致するので,ただちに解が与えられたような形になることがわかりますね.
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/14(Tue) 14:03)
Yokkunさん,返答ありがとうございます. 詳細な説明ありがとうございます. 力学的エネルギーから見るという考えがなかったので,新たな視点で見ることができました. 物理の問題を解くのは苦手ですか,色々な考えで物事をみれるのは楽しいことだと思います.
mNejiさん,Yokkunさん, 最後まで見ていただきありがとうございます. 自分の説明不足や単純なミスなどで大変ご迷惑をおかけしました. また何かわからない問題があった場合,また御教授願えるととても助かります. ありがとうございました.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/14(Tue) 15:46)
別解として,運動量と角運動量の運動方程式に基づいて円盤の微分方程式を出してみます.
座標について,
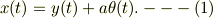
糸と円盤はすべらないから
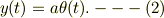
糸の左右の張力を,L,Rとすると,
錘の運動方程式
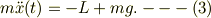
円盤の運動方程式
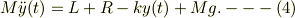
円盤の角運動量の運動方程式
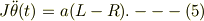
と計,5本の式が得られます.未知変数は,x,y,θ,L,Rの計5コなので解は得られます.
式(1),(2)より,座標は 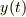 で表現出来るので,
で表現出来るので,
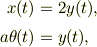
を用いて,
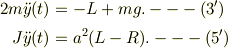
(4)を睨みながら,(3')*2 + (5')/a^2
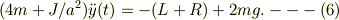
(4)+(6)
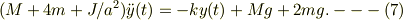
これを,ひろさんのNo.23470の式;
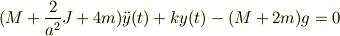
と比較すると,角運動量起源の項が「ファクター2」だけ違っている.恐らく,回転エネルギの項, 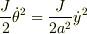 の
の 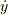 に付いての偏微分時に,分母の2を失念したものと思える.
に付いての偏微分時に,分母の2を失念したものと思える.
Re: 機械力学 バネ滑車
分からん さんのレス (2009/04/14(Tue) 19:24)
ばねに力が加わらない初期長さのときの,初期位置x(0)=0,y(0)=0,θ(0)=0 から円板から手を離すと,ばね力は0に等しいので, 円板とおもりは共に重力加速度で落下し始め,糸は必ずタルムのではないですか.
Re: 機械力学 バネ滑車
Yokkun さんのレス (2009/04/15(Wed) 01:34)
分からんさん,こんばんは.ご指摘にどっきりして計算してみると,まさにその通りのような気がします.導出された運動方程式で計算してみると,円板の初期加速度は4g/7.するとおもりの初期加速度は8g/7と重力加速度を超えてしまいます.つまり,張力L=-mg/7<0となってしまいますね.するとまずは糸がたるんだ状態でおもりが自由落下で円板は単振動.糸が伸びきった後からともに単振動…ということになりそうです.ひろさーん.@@;
mNejiさん,やはり束縛力を考慮した運動方程式の立式は重要ですね. 出題の流れからすると,これは明らかに出題者が考慮しなかった問題の不備ではないでしょうか?
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/15(Wed) 01:55)
分からんさん,ご指摘ありがとうございます. Yokkunさん,確かめていただきありがとうございます. この問題の答えがないので,問題の不備ということは明言できないのが現状です. ここ数年の問題から見ても,ここまで難しい問題は出題されていないので不備だとは思われます. この問題の正確な答えは,場合分けをするということでしょうか?
mNejiさん,別解ありがとうございます. 同じ問題でもアプローチの方法は色々あるということが実感できました. 自分は物理は苦手なほうなので,1つの問題を1通りでしか解く力が無く,mNejiさんみたいに解くことが出来る人をうらやましく思います.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/15(Wed) 09:57)
昨日は野暮用のお蔭で拝見出来ませんが,激変しているのに驚きました.
自分も定性的に考えて見ましたが,この問題の初期条件からすると,どうしても自由落下から動き始めると思う様になりました.すると,問題はとても複雑になってしまうようで,自分の力では解けるかどうかも定かでありません.ただ,少し冷静になって,この場合を検討してみます.
他方,折衷案かもしれませんが,糸が弛まない所まで円盤を引き下ろし,静止状態から離す場合がどうなるかを知りたい所です.
いずれにしろ,私には,この問題には啓発される点が多々ありました.がしかし,『入試問題』とすると試験の実施側には反省はあってしかるベキと思います.本来は,出題者側から釈明をするのが筋だと思えます.でも,この事件があった後には,平易な問題にシフトされたのでしょうね.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/15(Wed) 15:26)
単純な振動解がある場合の探索.
No.23485の式に基づいて考えます.
運動方程式(7)
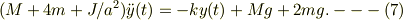
で,
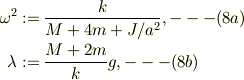
とすると,
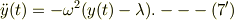
初期条件を緩めて, 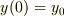 とします.
とします. 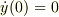 はそのままとします.すると,(7')の解は,
はそのままとします.すると,(7')の解は,
![y(t) &= \frac{y_0 -\lambda}{2}[\exp(\mathrm{i}\omega t)+\exp(-\mathrm{i}\omega t)] +\lambda,\\&= (y_0 -\lambda)\cos(\omega t) +\lambda, ---(8)](http://hooktail.maxwell.jp/bbslog/43d31ae63a78bed811d386efe79b5a2f.png)
となり,その時間微分は,
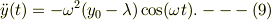
張力L,Rを求める為に,
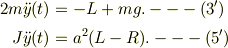
等に,(9)を適用して,
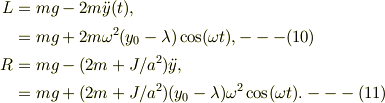
これから,「振動中に張力が常に正」の条件は出そうですね.
式(10)に対して「L > 0」の条件を与えると,余弦の項が±1の範囲である事に注意して,さらに  の正負で条件分けをした結果,
の正負で条件分けをした結果,
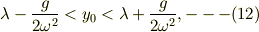
という限定条件が在る様です.この範囲を逸脱すると「L <= 0」となって,自由落下運動に入ると思われます.
#ただし,本来の目的, 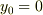 を排除出来ていない様な気がする.その為には,「
を排除出来ていない様な気がする.その為には,「 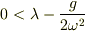 」が必要だが....
」が必要だが....
「R > 0」の場合も,類似の限定条件が得られる事でしょう.
ただ,この手の論議を細かくしても,あまり有意義な事にはならないと思うので,これで終了とします.
〜〜〜〜 こうしてみますと,ラグランジュ形式の解析で,張力を評価する方法論はないものかが気になり出しました.
Re: 機械力学 バネ滑車
ひろ さんのレス (2009/04/18(Sat) 00:05)
mNejiさん,評価ありがとうございます. 返答が遅れてしまって大変申し訳ありません.
このような大変な評価が必要になるとは想像もしてませんでした. 自分でも(12)式を導こうと思いましたが,なかなか思い通りになりません. cosがとても邪魔で難しいですね.数学の不等号処理が難しいことに,より気付くことになってしまいました.
Re: 機械力学 バネ滑車
mNeji さんのレス (2009/04/18(Sat) 16:37)
>このような大変な評価が必要になるとは想像もしてませんでした.
そうですね,院試験の問題として出されるとしても,ちょっと落とし穴の度が過ぎたかも知れません.
でも,分からんさんのように,「定性的な視点からの検証を心がける」事の大切さを知る良い経験を積まれたと思って,今後の研鑽に活かされるといいですね.
一寸,時期を失ったのですが,重力ポテンシャルの符号を取り違えた点にコメントします.
例えば,錘の重力ポテンシャルをG(x)とします.重力F(x)=mgであるとともに,
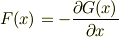
であることを注意しておけば, 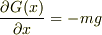 となるので,容易に;
となるので,容易に;
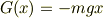
ですね.
#私は,頻繁にこのケアレス・ミスをしていますが...(泣).
これに懲りずに,確りと前進されますように.
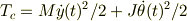
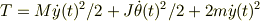
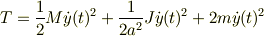
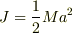 なので
なので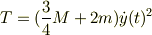
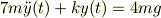
![y(t) = -\frac{4mg}{k} cos(\sqrt[]{\frac{k}{7m}} t) +\frac{4mg}{k}](http://hooktail.maxwell.jp/bbslog/d43e8ca6e0d1071ee9ba0ddba7e015d4.png)