スト−クスの面積分
スト−クスの面積分
数学迷い人↓ さんの書込 (2009/04/09(Thu) 14:57)
いつもすみませんが,お願いします.
xy面上の円C:x^2+y^2=1にそっての,ベクトルA=(x^2+y,x^2+2z,2y)の線積分 ∫A・drを計算する.
これをストークスの定理により面積分に変換して計算してみたいのですが,
∬(0,0,2x-1)・ndS とやっていったのですが,ここまで合っていますか? また,この先の計算の仕方がわからないのですが,教えて頂けないでしょうか?
円筒座標系とアドバイスをもらったのですが,良くわからないです.
とりあえず,∬(0,0,2x-1)・ndS が合ってるか気になります.
Re: スト−クスの面積分
ASA さんのレス (2009/04/09(Thu) 19:16)
B=rotAで計算して,たぶんあってると思います.n=(0,0,1)だから,z成分だけの計算ですみますよ.
Re: スト−クスの面積分
リモコン さんのレス (2009/04/09(Thu) 19:29)
ベクトル関数とnとの内積計算します(もともと回転がz成分だけになってしまいましたが・・・) 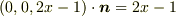 です.
です.
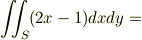
とちょくせつx,yで計算てもいいのですが,円筒座標(r,θ,z)使うと,確かに計算が簡単です.(x,y,z)=(rcosθ,rsinθ,z)です.ヤコビアンは
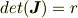
になります.ヤコビアンがわからなかったら調べてください.
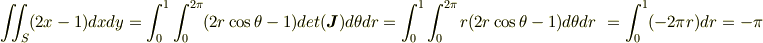
となります.
Re: スト−クスの面積分
toorisugari no Hiro さんのレス (2009/04/09(Thu) 19:39)
ううむ.本当に高校生?:-) 100点満点の回答ですね.
なお,今回の場合も領域の対称性を考えれば,奇関数の性質が使えて
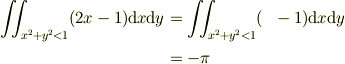
とできますね.
Re: スト−クスの面積分
リモコン さんのレス (2009/04/09(Thu) 22:16)
なるほど!!普通のx軸上のみの積分と同様,奇関数,偶関数の性質を使うことが出来るとは,これは凄いですね.積分計算があっさり(−1)*(円の面積)になってしまいましたね.
高校の物理で,電磁気学をやるのですが,ネットで調べると,当時では意味不明な記号(rot,div,面積分とか)が電磁気学では出てくるので,ネットや近くの私立工業大学の図書館なんかを利用して,ベクトル解析を独学したら面白くなってしまったんですよ.今日から大学受験生になるので,しばらくは高校の授業に集中することになりますが・・・・
ですからまだ簡単な微分方程式くらいしか解けませんし,ベクトル解析は物理的にしかとらえられていません.数学的厳密な証明は詳しく学んでいません...
Re: スト−クスの面積分
mNeji さんのレス (2009/04/09(Thu) 23:13)
リモコンさん,
ちょっと割り込みモードで失礼します.
高校生で,かつ独学で,此処までご自分で理解されたという事はとても素晴らしいと思います.
敢えて言わせて頂ければ,物理を慌てて学ぶよりは,作文・英語・数学,化学・生物,歴史・地理といった基礎能力や他分野を広く収めたらと思います.その上で,物理の探求に入られたらと思います.
また,人間,勉学や仕事についての能力も大事だと思いますが,生きる上の余裕,趣味とか運動も大切かと思います.個人のなかでも,バランス感覚が必要かと思います.
一老人の反省の弁ですが...(笑).
【追伸】
でも,此処まで短期間にベクトル解析を学ばれたのですから,本に頼らずに「ご自分なりの考え方」を気晴らしにトライされるのも良いかと.それで,問題にぶつかったら,喜んで論議下さる方々がいらっしゃると思います.;-p)
Re: スト−クスの面積分
ASA さんのレス (2009/04/10(Fri) 07:08)
>積分計算があっさり(−1)*(円の面積)になってしまいましたね. 単位円の面積S=∬dxdy=∬rdrdθ=πであることを利用すれば,今の計算ではあまり変りませんね. xが奇関数で初項を消すか,cosθの正負振動で初項を消すかの違いでしかないです(別のところで(cosθ)^2nの積分について値を示してあるので参考に). (x,y)で考えると変数端がy=sqr(1-x^2)となり,∫sqr(1-x^2)dxの計算が面倒だったりしますな.
Re: スト−クスの面積分
数学迷い人↓ さんのレス (2009/04/10(Fri) 10:07)
重積分は単純に順番にやっていけば良いんですよね?
ちなみに,内側同士と外側同士が対応しているんですよね? で,順番は,先に内側,次に外側ですよね?これか決まりですか?
ヤコビ行列は証明なしで,いきなりdxdy=Jdrdθと入試で使えますか?
Re: スト−クスの面積分
toorisugari no Hiro さんのレス (2009/04/10(Fri) 10:15)
> 重積分は単純に順番にやっていけば良いんですよね?
私が書いたのは「裏技」で,まじめにやると,
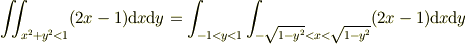
を計算しなければならず,まあ大変です(それでも履修範囲内なので,ぜひ計算してほしいですが).
ASAさん,リモコンさんがやられたように極座標で考えるのが基本です.
Re: スト−クスの面積分
ASA さんのレス (2009/04/10(Fri) 12:18)
数学迷い人さん
迷宮からなかなか抜けられませんね.
>重積分は単純に順番にやっていけば良いんですよね? 順番はお好きなように.面積を求めることをイメージすれば,縦長の短冊で区切ろうが横長の短冊で区切ろうが同じことが理解できるでしょう.
>ヤコビ行列は証明なしで,いきなりdxdy=Jdrdθと入試で使えますか? ヤコビなんて無視してOKです.dxをdrと対応させるとき,dyはrdθと対応することが理解できればよろしいでしょう.