光子について
光子について
help me さんの書込 (2009/04/09(Thu) 01:40)
光子についていくつか質問があります.
1.なぜ光子は陽電子と電子には崩壊できるのに,一個の電子には崩壊できないのか?
2.光子のエネルギーが5MeVだとすると各々の粒子の運動エネルギーはいくらになるのか.
3.また,それらの粒子が光の速度に近いことを示す.
以上3点です.見当もつかない状態に近いのでどなたか教えてください.
1については光子は中性なので負の電荷を持つ電子のみに崩壊しては中性のバランスが崩れる的なことなのでしょうか? 2,3はよくわからないです.どのような式を使えば求まるのでしょうか?
よろしくお願いします.
Re: 光子について
toorisugari no Hiro さんのレス (2009/04/09(Thu) 09:20)
- そのような考察で良いと思います.他に理由は考えられますか?
- 「各々の粒子」が不明ですが,電子ですか?
- 相対論的な運動量とエネルギーの定義式は?
> どのような式を使えば求まるのでしょうか?
2.,3.については教科書に書いてあるはずです.
Re: 光子について
ASA さんのレス (2009/04/09(Thu) 09:49)
>1.なぜ光子は陽電子と電子には崩壊できるのに,一個の電子には崩壊できないのか? 物理的イメージの問題ですが,光子は複合物でないと考えてます. 場を励起して,陽電子と電子に分解するのに,ある程度のエネルギーが必要とみます.つまり光子は電磁エネルギーの塊にすぎないというイメージです.
Re: 光子について
toorisugari no Hiro さんのレス (2009/04/09(Thu) 23:15)
>1.なぜ光子は陽電子と電子には崩壊できるのに,
つっこむと,2個ならともかく,一個の光子では「陽電子と電子には崩壊でき」ないはずです.
4元ベクトルを 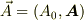 と書くことにし,光子の4元運動量ベクトルを
と書くことにし,光子の4元運動量ベクトルを 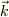 ,陽電子と電子の4元運動量ベクトルを
,陽電子と電子の4元運動量ベクトルを 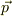 ,
, 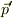 とすると,エネルギー運動量保存則は
とすると,エネルギー運動量保存則は
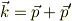
となるので,
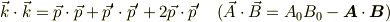
これと質量  と4元運動量ベクトル
と4元運動量ベクトル 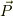 の関係式
の関係式
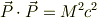
を組み合わせると
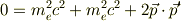
となり,陽電子と電子の4元運動量ベクトルが「時間的」である条件
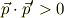
に矛盾します.
Re: 光子について
ASA さんのレス (2009/04/10(Fri) 07:53)
さらに突っ込むと, 光子2個なら矛盾しないということになりますね. 何もないところで2つの光子をぶつけると,陽電子と電子には崩壊するということでしょうか? もし,崩壊するなら重ね合わせと矛盾しないでしょうか?
Re: 光子について
toorisugari no Hiro さんのレス (2009/04/10(Fri) 08:41)
あくまでも,相対論的制限のみで考えていますが,「2つの光子をぶつけると,陽電子と電子には崩壊する」は運動量保存則と質量定義式,および,正質量粒子は「(未来)時間的」であるという制限,には矛盾しないようにできます.
ただ,仮想粒子を含めた中間状態がどうなっているか,とかのQED的知識はないので,「光子同士が電磁相互作用するようにみえるので矛盾ではないか?」「『空間的』電子が出てくるのは変ではないか?」などといった話は分かりません.よろしければ,教えてください.
# 中性粒子を媒介に考えると難しいことは考えなくて済みますが,QEDではないですしね.
Re: 光子について
ASA さんのレス (2009/04/10(Fri) 12:31)
衝突(散乱)プロセスとして理解してます.k:光子,Y:粒子,n:生成反粒子,n_:生成反粒子 弾性衝突(コンプトン散乱);k+Y→k'+Y' 非弾性弾性衝突;k+Y→k'+Y'+(n+n_) Yを無視して考えると,k→k'+(n+n_)と崩壊のように見え,かつ,保存則を破っているようにみえるということですね. 普通の粒子崩壊では,寿命とかがあります.