今度は計算が・・・

今度は計算が・・・

数学迷い人↓ さんの書込 (2009/04/08(Wed) 12:30)

∫｛-sinx(cosx)^2-(sinx)^2+(cosx)^3｝dx（０〜2πでの定積分）

はどのように計算すればいいのでしょうか？

たしか，sinかcosに統一すると思うのですが，統一しても，余計複雑になってしまって，計算が進めませんでした．

計算の仕方を教えてください．お願いします．

Re: 今度は計算が・・・

toorisugari no Hiro さんのレス (2009/04/08(Wed) 13:15)

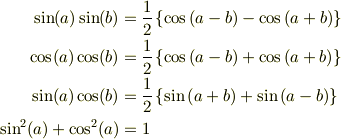
\sin(a)\sin(b) &= \frac{1}{2}\left\{ \cos\left({a-b}\right) - \cos\left({a+b}\right) \right\}\\\cos(a)\cos(b) &= \frac{1}{2}\left\{ \cos\left({a-b}\right) + \cos\left({a+b}\right) \right\}\\\sin(a)\cos(b) &= \frac{1}{2}\left\{ \sin\left({a+b}\right) + \sin\left({a-b}\right) \right\}\\\sin^2(a)+\cos^2(a) &=1

を組み合わせて，被積分関数を

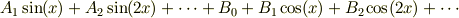
A_1\sin(x) + A_2\sin(2 x) + \cdots + B_0 + B_1\cos(x) + B_2\cos(2 x) + \cdots

の形にします． 0から 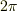2\pi までの定積分なら 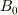B_0 の項以外は落ちて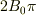， 2B_0\pi が求める答えになります．

Re: 今度は計算が・・・

数学迷い人↓ さんのレス (2009/04/08(Wed) 13:25)

回答ありがとうございます．

しかし，これは次数を下げた後の処理ということでは・・・？

次数の下げ方の良い方法が見つかりません．その点について，もう一度お願いします．お手数かけて申し訳ありません．

Re: 今度は計算が・・・

ASA さんのレス (2009/04/08(Wed) 14:11)

周期性と偶奇性から即断すると∫(sinx^2)dxしか残らないと思います． で，山と谷の面積は等しいので1/2，山のピークは1，幅が2πなのでこれらを掛け合わせてπと目算します． (∫(sinx)^2n dx=∫(cosx)^2n dx=π,∫(sinx)^(2n-1) dx=∫(cosx)^(2n-1) dx=0, ,∫sinx(cosx)^2n dx=∫cosx(sinx)^2n dx=0等は，暗記しておくと便利です．)

Re: 今度は計算が・・・

ASA さんのレス (2009/04/08(Wed) 14:22)

あと，関数基底としての直交性から∫sin(x)sin(mx)dx=0等も便利な公式ですね．

Re: 今度は計算が・・・

数学迷い人↓ さんのレス (2009/04/08(Wed) 14:25)

これらの公式は，大学院入試などで，証明せずに用いてもいいのでしょうか？

Re: 今度は計算が・・・

toorisugari no Hiro さんのレス (2009/04/08(Wed) 15:00)

> これは次数を下げた後の処理ということでは・・・？

いいえ，次数を下げる処理ですよ．

> これらの公式は，大学院入試などで，証明せずに用いてもいいのでしょうか？

大学院入試だったら，問題の文脈次第でしょう．倍角の公式等は証明は必要ないですが，物理・数学系ならこれくらい基礎事項からいつでも証明できますよね．

Re: 今度は計算が・・・

リモコン さんのレス (2009/04/08(Wed) 18:08)

一応高校生なりに全部計算して丁寧にやると

三倍角，二倍角の式

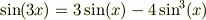
\sin(3x)=3\sin(x)-4\sin^3(x)
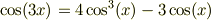
\cos(3x)=4\cos^3(x)-3\cos(x)
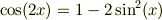
\cos(2x)=1-2\sin^2(x)

を使うと，被積分関数の次数が下がり，答えが出ました． 本当にASAさんの言ったとおり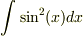， \int \sin^2(x)dx にまとまりました． ASAさんが紹介した覚えるべき数式は帰納法以外で証明できるものなのでしょうか

Re: 今度は計算が・・・

toorisugari no Hiro さんのレス (2009/04/08(Wed) 20:04)

ン? > ∫(sinx)^2n dx=∫(cosx)^2n dx=π って本当ですか?

n=2ですでに違う値になりますが．

あと，細かいですが， > ∫sin(x)sin(mx)dx=0

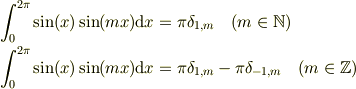
\int_{0}^{2\pi}\sin(x)\sin(m x)\mathrm{d} x &= \pi \delta_{1,m} \quad(m\in\mathbb{N})\\\int_{0}^{2\pi}\sin(x)\sin(m x)\mathrm{d} x &= \pi \delta_{1,m} -\pi \delta_{-1,m}\quad(m\in\mathbb{Z})

ですよね．

Re: 今度は計算が・・・

ASA さんのレス (2009/04/08(Wed) 20:52)

>> ∫(sinx)^2n dx=∫(cosx)^2n dx=π >n=2ですでに違う値になりますが． 検算してみると，確かに山と谷が非対称になってますね． ピークが鋭く，谷が緩やかと．撤回します．

Re: 今度は計算が・・・

ASA さんのレス (2009/04/09(Thu) 12:20)

たぶん∫(sinx)^2n dx=∫(cosx)^2n dx=2π(2n-1)!!/2n!!:5!!=5*3*1,6!!=6*4*2 だと思います．識者の方検算をお願いします．

Re: 今度は計算が・・・

toorisugari no Hiro さんのレス (2009/04/09(Thu) 12:48)

> たぶん∫(sinx)^2n dx=∫(cosx)^2n dx=2π(2n-1)!!/2n!!:5!!=5*3*1,6!!=6*4*2 だと思います．

数学ソフトで検算した結果(直接解を出す方法を知らない．．．)，n=1,...10,100,500で

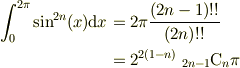
\int_0^{2\pi} \sin^{2n}(x)\mathrm{d}x &= 2\pi \frac{(2n-1)!!}{(2n)!!}\\&= 2^{2(1-n)}~_{2n-1}\mathrm{C}_{n}\pi

であっているみたいです．

参考のため，導出過程を教えてもらえませんか?

Re: 今度は計算が・・・

なんとなく さんのレス (2009/04/09(Thu) 13:40)

横から失礼． In=∫sin^2n(x)dxとおけば，部分積分で， In=[-cos(x)sin^(2n-1)(x)]+(2n-1)∫cos^2(x)sin^(2n-2)(x)dx =(2n-1){In-1-In} ∴In=(2n-1)/2n・In-1・・・=(2n-1)!!/(2n)!!・I0=2π・(2n-1)!!/(2n)!! In=∫cos^2n(x)dxも同じ． で良いんではないですか？

Re: 今度は計算が・・・

toorisugari no Hiro さんのレス (2009/04/09(Thu) 22:03)

なんとなくさん，ありがとうございます．

Re: 今度は計算が・・・

ASA さんのレス (2009/04/10(Fri) 13:12)

ついでだから，tanについても書いておきます． たぶん∫(tanx)^2n dx={?[i=1,n]{(-)^i(tanx)^(2i-1)/(2i-1)}+x}(-)^n 処方;(tanx)^2=(secx)^2-1 と(tanx)'=(secx)^2を利用して漸化式を作る．